3.6: The Microscope
( \newcommand{\kernel}{\mathrm{null}\,}\)
The front lens of a microscope is generally called the “objective” lens, rather than the “object glass”. In contrast to the telescope, the objective is a small lens with a short focal length. The object is placed just outside the focal point of the objective, and a magnified real inverted primary image is formed quite some distance away. This is examined with an eyepiece in the same way that the primary image formed in a telescope is examined with an eyepiece. As discussed for the telescope eyepiece, the eyepiece in reality has a second lens (the “field lens”), which I have not drawn, which almost (but not quite) coincides with the primary in order to bend that vexing ray towards the centre of the eye lens. The primary image is in the focal plane of the eyepiece, but (unlike for the telescope) it is not in the focal plane of the objective,
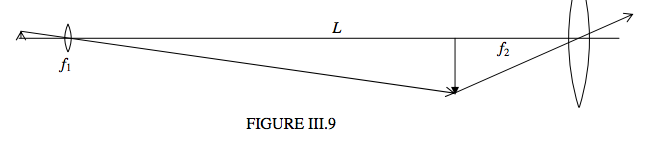
Everyone knows how to calculate the angular magnification produced by a magnifying glass (D/f) and by a telescope (f1/f2). A microscope isn’t quite so easy, which is why, in an exam, you will be asked for the magnification of a microscope rather than of a magnifying glass or a telescope. When you are focussing a telescope, you pull the eyepiece in and out until the image appears in focus for your relaxed eye. When you are focussing a microscope, however, rather than moving just the eyepiece, you move the whole microscope tube up and down, in such a manner that the distance L between the two lenses is constant. What we need, then, is to find the magnification in terms of the two focal lengths and the distance L between the lenses.
Recall the way a microscope works. First, the objective produces a magnified real image of the object. Then you look at this primary image with an eyepiece. The overall magnification, then, is the product of the linear magnification produced by the objective and the angular magnification produced by the eyepiece. We shall address ourselves to these two in turn.
To find the linear magnification produced by the objective, we need to know the object and image distances. The image distance is just L−f2, and, since the focal length of the objective is f1, it doesn’t take us a moment to find that the object distance is
f1(L−f2)L−f1−f2.
Therefore the linear magnification produced by the objective is
L−f1−f2f1.
And the angular magnification produced by the eyepiece is just D/f2, where D is the distance to the near point (25 cm). Thus the overall angular magnification is
L−f1−f2f1×Df2.
Voilà! It’s easy!


