Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

2.11: Thick Lenses

Last updated

Mar 5, 2022
Save as PDF
- 2.10: Designing an Achromatic Doublet
- 2.12: Principal Planes

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Figure II.16 shows a thick lens of index $n_2$ , an object O and an image I. For good measure I have put a medium of index $n_1$ to the left of the lens and a medium of index $n_3$ to the right of the lens.

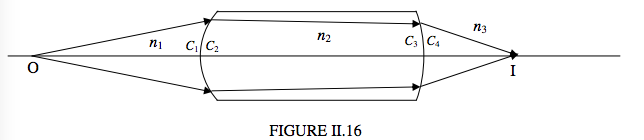
FIGURE II.16.png

If you are given the position of O, can you calculate the position of the image?

Well, it is easy to calculate the convergence $C_1$ when the light arrives at the first surface. Then we can easily calculate the convergence $C_2$ merely by adding the power of the first interface. And, if we know $C_3$ (Aye, there’s the rub) we can easily calculate $C_4$ . We see that the key to solving thick lens problems is to know how convergence changes with distance, so we shall make that our next aim.

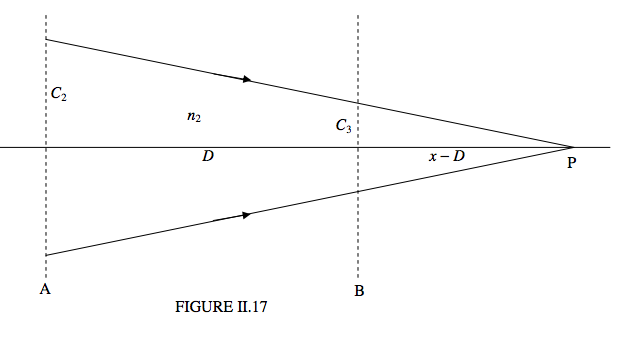
FIGURE II.17 .png

Figure II.17 shows a beam of light, in a medium of index $n_2$ , converging to the point P, which is at a distance $x$ from the plane A. The convergence of the beam as it leaves the plane A is $C_2 = n_2/x$ . When it arrives at the plane B, which is at a distance D from the plane A, its convergence is $C_3 =n_2/(x-D)$ . When we eliminate $x$ , we obtain

$C_3 = \frac{n_2C_2}{n_2 - DC_2} \label{eq:2.11.1}$

for the formula that tells us how convergence changes with distance.

Let us now return to the problem of Figure II.16.

Example $\PageIndex{1}$

Let’s suppose that the radii of curvature of the first and second faces are 15 and 25 cm respectively, and the distance between the faces is 50 cm. The refractive index of the glass is $n_2$ = 1.60. We’ll suppose that there is water ( $n_1$ = 1.33) to the left of the lens, and, to the right of the lens there is some liquid with refractive index 1.42. The object is 30 cm to the left of the first face. Where is the image?

Solution

The calculation goes as follows (Equation $\ref{eq:2.11.1}$ ):

$\begin{align*} C_1 &= -\dfrac{1.33}{30} = -0.044333 \, \text{cm}^{-1} \\[4pt] C_2 &= C_1 + \dfrac{1.60-1.33}{+15} = -0.026333 \, \text{cm}^{-1} \\[4pt] C_3 &= \dfrac{1.60\times C_2}{1.60 - 50 \times C_2} = -0.014446 \, \text{cm}^{-1} .\end{align*}$

Notice that the light is diverging by the time that it reaches the second face.

$C_4 = C_3 + \dfrac{1.42-1.60}{-25} = -0.007246 \, \text{cm}^{-1}. \nonumber$

The light is still diverging, so the image is virtual. The distance of the image from the second face is 1.42 ÷ 0.007 246 = 196 cm, and it is to the left of the second face.

The magnification of a thick lens is easily found. The magnification produced by the first face is, as usual, $C_1/C_2$ , and then there is a further magnification of $C_3/C_4$ produced by the second face. Thus the overall magnification is $\frac{C_1C_3}{C_2C_4}$ , which is this case is +3.356. The image is magnified in size and it is erect.

This method for thick lenses can also be used for separated lenses and mirrors. Here’s one:

Example $\PageIndex{2}$

Figure II.18 shows a thin lens separated from a mirror, and an object 14 cm from the lens. Where is the image?

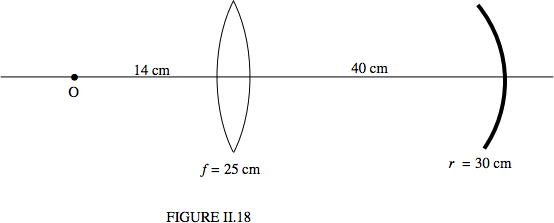
Solution

$C_1 = -1/14 = -0.071420$ cm^-1.

$C_2 = C_1 +1/25 = -0.031429$ cm^-1.

$C_3 = \frac{C_2}{1-40\times C_2}=-0.013924$ cm^-1.

$C_4 = C_3 + \frac{-2}{-30} =+0.053743$ cm^-1.

The image is real. It is 18.96 cm to the left of the mirror. The magnification is −0.60. The image is inverted and diminished.

Of course those who set examinations can think of all sorts of unpleasant questions. For example, we might have a thick lens and an object, but, instead of being asked to find the image, we may be told the image distance and asked to find the refractive index, or the thickness, or one of the radii. Or, even worse, we might not be told the image distance, but we might be told its magnification and whether it is real or virtual, or erect or inverted, and asked to find something else. There are endless possibilities! Here’s one.

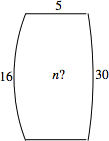
The lens shown has radii of curvature 16 and 30 cm, and is 5 cm thick. An object is 36 cm to the left of the 16 cm face. Its image is 50 cm to the right of the 30 cm surface. Show that the refractive index is the positive solution of

$1845n^2 - 2417n - 520 = 0$ .

Here's another one.

Example $\PageIndex{2}$

The lens shown is 4 cm thick and the refractive index is 1.6. The radius of curvature of the first face is 15 cm. An object is 32 cm to the left of the 15 cm face. Its image is real, inverted and magnified by 22. Determine the radius of curvature of the second face.

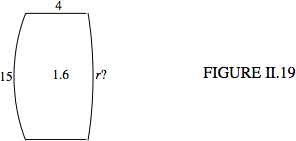
Solution

Hints. The image is real. Which side of the lens is it? You can easily calculate $C_1 , C_2$ and $C_3$ , so you should be able to get $C_4$ from the magnification. The answer, by the way, is 80.1 cm – but is it convex to the right, as shown, or is it concave to the right?

One more.

Example $\PageIndex{4}$

The two lenses are made of a very light solid whose refractive index is only 1.3. (I’m not sure if there is such a stuff!) and they are immersed in a liquid of index 1.4. That means that the convex lens is diverging. The second surface of the second lens is a reflecting mirror. I have indicated the radii of curvature, and the lenses are 40 cm apart. Parallel light comes from the left. Where does it come to a focus?

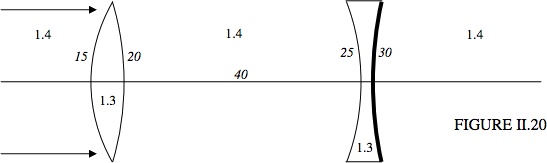
Solution

The initial convergence $C_1 = 0$ . I’ll calculate the convergence after the light arrives at or leaves each surface or interface. I hope the notation will be clear. All convergences are in cm⁻¹.

$\begin{align*} C_2 &= 0 + \dfrac{1.3-1.4}{+15} = -0.006. \\[4pt] C_3 &= -0.006 + \dfrac{1.4-1.3}{-20} = -0.0116. \\[4pt] C_4 &= \dfrac{1.4C_3}{1.4-40C_3} = -0.00875.\\[4pt] C_5 &= -0.00875 + \dfrac{1.3-1.4}{-25} = -0.00475.\\[4pt] C_6 &= -0.00475 + \dfrac{-2\times 1.3}{30} =-0.091416. \\[4pt] C_7 &= -0.091416 + \dfrac{1.4-1.3}{+25} = -0.087416.\\[4pt] C_8&=\dfrac{1.4C_7}{1.4-40C_7} = -0.02499319265.\\[4pt] C_9 &= C_8 + \dfrac{1.3-1.4}{-20} = -0.02999319265.\\[4pt] C_{10} &= C_9 + \dfrac{1.4-1.3}{-15} = -0.03665985931. \end{align*}$

Finally, $C_{10} = \frac{1.4}{x}$ , so $x = -38.188 908 15 \left(=-\frac{22035}{577}\right)$ cm.

That is, the focus is 38.2 cm to the right of the convex lens, or 1.8 cm to the left of the concave lens.

Exercise $\PageIndex{1}$

Compose a problem in which a student is given the focal length of two lenses, and the positions of object and image, and the student is asked to calculate the distance between the lenses.

Support Center

How can we help?