2.1: Accelerators
( \newcommand{\kernel}{\mathrm{null}\,}\)
Resolving power
Both nuclear and particle physics experiments are typically performed at accelerators, where particles are accelerated to extremely high energies, in most cases relativistic (i.e., v≈c). To understand why this happens we need to look at the role the accelerators play. Accelerators are nothing but extremely big microscopes. At ultrarelativistic energies it doesn’t really matter what the mass of the particle is, its energy only depends on the momentum:
E=hν=√m2c4+→p2c2≈pc
from which we conclude that
λ=cν=hp.
The typical resolving power of a microscope is about the size of one wave-length, λ. For an an ultrarelativistic particle this implies an energy of
E=pc=hcλ
| particle | scale | energy |
|---|---|---|
| atom | 10−10m | 2 keV |
| nucleus | 10−14m | 20 MeV |
| nucleon | 10−15m | 200 MeV |
| quark? | <10−18m | >200 GeV |
You may not immediately appreciate the enormous scale of these energies. An energy of 1 TeV (=1012eV) is 3×10−7 J, which is the same as the kinetic energy of a 1g particle moving at 1.7 cm/s. And that for particles that are of submicroscopic size! We shall thus have to push these particles very hard indeed to gain such energies. In order to push these particles we need a handle to grasp hold of. The best one we know of is to use charged particles, since these can be accelerated with a combination of electric and magnetic fields – it is easy to get the necessary power as well.
Types
We can distinguish accelerators in two ways. One is whether the particles are accelerated along straight lines or along (approximate) circles. The other distinction is whether we used a DC (or slowly varying AC) voltage, or whether we use radio-frequency AC voltage, as is the case in most modern accelerators.
DC fields
Acceleration in a DC field is rather straightforward: If we have two plates with a potential V between them, and release a particle near the plate at lower potential it will be accelerated to an energy 12mv2=eV. This was the original technique that got Cockroft and Wolton their Nobel prize.
van der Graaff generator
A better system is the tandem van der Graaff generator, even though this technique is slowly becoming obsolete in nuclear physics (technological applications are still very common). The idea is to use a (non-conducting) rubber belt to transfer charge to a collector in the middle of the machine, which can be used to build up sizable (20 MV) potentials. By sending in negatively charged ions, which are stripped of (a large number of) their electrons in the middle of the machine we can use this potential twice. This is the mechanism used in part of the Daresbury machine.

Other linear accelerators
Linear accelerators (called Linacs) are mainly used for electrons. The idea is to use a microwave or radio frequency field to accelerate the electrons through a number of connected cavities (DC fields of the desired strength are just impossible to maintain). A disadvantage of this system is that electrons can only be accelerated in tiny bunches, in small parts of the time. This so-called “duty-cycle”, which is small (less than a percent) makes these machines not so beloved. It is also hard to use a linac in colliding beam mode (see below).
There are two basic setups for a linac. The original one is to use elements of different length with a fast oscillating (RF) field between the different elements, designed so that it takes exactly one period of the field to traverse each element. Matched acceleration only takes place for particles traversing the gaps when the field is almost maximal, actually sightly before maximal is OK as well. This leads to bunches coming out.

More modern electron accelerators are build using microwave cavities, where standing microwaves are generated. Such a standing wave can be thought of as one wave moving with the electron, and another moving the other wave. If we start of with relativistic electrons, v≈c, this wave accelerates the electrons. This method requires less power than the one above.
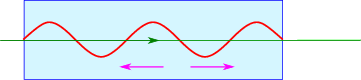
Figure 2.1.3: Acceleration by a standing wave
Cyclotron
The original design for a circular accelerator dates back to the 1930’s, and is called a cyclotron. Like all circular accelerators it is based on the fact that a charged particle (charge qe) in a magnetic field B with velocity v moves in a circle of radius r, more precisely
qvB=γmv2r,
here γm is the relativistic mass, γ=(1−β2)−1/2, β=v/c. A cyclotron consists of two metal “D”-rings, in which the particles are shielded from electric fields, and an electric field is applied between the two rings, changing sign for each half-revolution. This field then accelerates the particles.

The field has to change with a frequency equal to the angular velocity,
f=ω2π=v2πr=qB2πγm.
For non-relativistic particles, where γ≈1, we can thus run a cyclotron at constant frequency, 15.25 MHz/T for protons. Since we extract the particles at the largest radius possible, we can determine the velocity and thus the energy,
E=γmc2=[(qBRc)2+m2c4]1/2
Synchroton
The shear size of a cyclotron that accelerates particles to 100 GeV or more would be outrageous. For that reason a different type of accelerator is used for higher energy, the so-called synchroton where the particles are accelerated in a circle of constant diameter.

In a circular accelerator (also called synchroton), see Figure 2.1.5, we have a set of magnetic elements that bend the beam of charged into an almost circular shape, and empty regions in between those elements where a high frequency electro-magnetic field accelerates the particles to ever higher energies. The particles make many passes through the accelerator, at every increasing momentum. This makes critical timing requirements on the accelerating fields, they cannot remain constant.
Using the equations given above, we find that
f=qB2πγm=qBc22πE=qBc22π(m2c4+q2B2R2c2)1/2
For very high energy this goes over to
f=c2πR,E=qBRc,
so we need to keep the frequency constant whilst increasing the magnetic field. In between the bending elements we insert (here and there) microwave cavities that accelerate the particles, which leads to bunching, i.e., particles travel with the top of the field.
So what determines the size of the ring and its maximal energy? There are two key factors:
As you know, a free particle does not move in a circle. It needs to be accelerated to do that. The magnetic elements take care of that, but an accelerated charge radiates – That is why there are synchroton lines at Daresbury! The amount of energy lost through radiation in one pass through the ring is given by (all quantities in SI units) ΔE=4π3ϵ0q2β3γ4R
| proton | E | ΔE |
|---|---|---|
| 1 GeV | 1.5×10−11 eV | |
| 10 GeV | ||
| 100 GeV | 1.5×10−3 eV | |
| 1000 GeV | 1.5×101 eV | |
| electron | E | ΔE |
| 1 GeV | 2.2×102 eV | |
| 10 GeV | 2.2 MeV | |
| 100 GeV | 22 GeV | |
| 1000 GeV | 2.2×1015 GeV |
The other key factor is the maximal magnetic field. From the standard expression for the centrifugal force we find that the radius R for a relativistic particle is related to it’s momentum (when expressed in GeV/c) by
p=0.3BR
For a standard magnet the maximal field that can be reached is about 1 T, for a superconducting one 5T. A particle moving at p=1TeV/c=1000GeV/c requires a radius of
| B | p | R |
|---|---|---|
| 1 T | 1 GeV/c | 3.3 m |
| 10 GeV/c | 33 m | |
| 100 GeV/c | 330 m | |
| 1000 GeV/c | 3.3 km | |
| 5 T | 1 GeV/c | 0.66 m |
| 10 GeV/c | 6.6 m | |
| 100 GeV/c | 66 m | |
| 1000 GeV/c | 660 m |


