1.1: Linear Vector Spaces

Consider a set of vectors, denoted by \(|\psi\rangle,|\phi\rangle\), etc., and the complex numbers \(a, b, c\), etc. A linear vector space 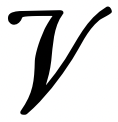is a mathematical structure of vectors and numbers that obeys the following rules:

1. \(|\psi\rangle+|\phi\rangle=|\phi\rangle+|\psi\rangle\) (commutativity),
2. \(|\psi\rangle+(|\phi\rangle+|\chi\rangle)=(|\psi\rangle+|\phi\rangle)+|\chi\rangle\) (associativity),
3. \(a(|\psi\rangle+|\phi\rangle)=a|\psi\rangle+a|\phi\rangle\) (linearity),
4. \((a+b)|\psi\rangle=a|\psi\rangle+b|\psi\rangle\) (linearity),
5. \(a(b|\phi\rangle)=(a b)|\phi\rangle .\)

There is also a null vector 0 such that \(|\psi\rangle+0=|\psi\rangle\), and for every \(|\psi\rangle\) there is a vector \(|\phi\rangle\) such that \(|\psi\rangle+|\phi\rangle=0\).

For each vector \(|\phi\rangle\) there is a dual vector \(\langle\phi|\), and the set of dual vectors also form a linear vector space 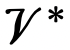. There is an inner product between vectors from 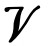and 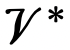denoted by \(\langle\psi \mid \phi\rangle\). The inner product has the following properties:

1. \(\langle\psi \mid \phi\rangle=\langle\phi \mid \psi\rangle^{*}\),
2. \(\langle\psi \mid \psi\rangle \geq 0\),
3. \(\langle\psi \mid \psi\rangle=0 \Leftrightarrow|\psi\rangle=0\),
4. \(|\psi\rangle=c_{1}\left|\psi_{1}\right\rangle+c_{2}\left|\psi_{2}\right\rangle \Rightarrow\langle\phi \mid \psi\rangle=c_{1}\left\langle\phi \mid \psi_{1}\right\rangle+c_{2}\left\langle\phi \mid \psi_{2}\right\rangle\),
5. \(\|\phi\| \equiv \sqrt{\langle\phi \mid \phi\rangle} \text { is the norm of }|\phi\rangle\).

If \(\|\phi\|=1\), the vector \(|\phi\rangle\) is a unit vector. The set of unit vectors \(\left\{e^{i \varphi}|\psi\rangle\right\}\) with \(\varphi \in[0,2 \pi)\) form a so-called ray in the linear vector space. A linear vector space that has a norm \(\|.\|\) (there are many different ways we can define a norm) is called a Hilbert space. We will always assume that the linear vector spaces are Hilbert spaces.

For linear vector spaces with an inner product we can derive the Cauchy-Schwarz inequality, also known as the Schwarz inequality:

\[|\langle\phi \mid \psi\rangle|^{2} \leq\langle\psi \mid \psi\rangle\langle\phi \mid \phi\rangle\tag{1.1}\]

This is a very important relation, since it requires only the inner product structure. Relations that are based on this inequality, such as the Heisenberg uncertainty relation between observables, therefore have a very general validity.

If two vectors have an inner product equal to zero, then these vectors are called orthogonal. This is the definition of orthogonality. When these vectors are also unit vectors, they are called orthonormal. A set of vectors \(\left|\phi_{1}\right\rangle,\left|\phi_{2}\right\rangle, \ldots\left|\phi_{N}\right\rangle\) are linearly independent if

\[\sum_{j} a_{j}\left|\phi_{j}\right\rangle=0\tag{1.2}\]

implies that all \(a_{j}=0\). The maximum number of linearly independent vectors in 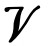is the dimension of 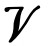. Orthonormal vectors form a complete orthonormal basis for 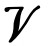if any vector can be written as

\[|\psi\rangle=\sum_{k=1}^{N} c_{k}\left|\phi_{k}\right\rangle\tag{1.3}\]

and \(\left\langle\phi_{j} \mid \phi_{k}\right\rangle=\delta_{j k}\). We can take the inner product of \(|\psi\rangle\) with any of the basis vectors \(\left|\phi_{j}\right\rangle\) to obtain

\[\left\langle\phi_{j} \mid \psi\right\rangle=\sum_{k=1}^{N} c_{k}\left\langle\phi_{j} \mid \phi_{k}\right\rangle=\sum_{k=1}^{N} c_{k} \delta_{j k}=c_{j}\tag{1.4}\]

Substitute this back into the expansion of \(|\psi\rangle\), and we find

\[|\psi\rangle=\sum_{k=1}^{N}\left|\phi_{k}\right\rangle\left\langle\phi_{k} \mid \psi\right\rangle\tag{1.5}\]

Therefore \(\sum_{k}\left|\phi_{k}\right\rangle\left\langle\phi_{k}\right|\) must act like the identity. In fact, this gives us an important clue that operators of states must take the general form of sums over objects like \(|\phi\rangle\langle\chi|\).