13.6: The Hydrogen Atom
( \newcommand{\kernel}{\mathrm{null}\,}\)
The potential that an electron in a Hydrogen atom experiences results from the electrostatic interaction between the electron (which is negatively charged) and the proton (which is positively charged). (A Hydrogen nucleus is composed of a single proton.) It is traditional (and convenient) to choose the zero level of the potential to be when the electron is extremely far away from the proton. This means that the potential energy gets more and more negative as the electron gets closer and closer to the proton. The form of this potential is:
V(r)=−14πϵ0e2r
In this equation, ϵ0 is a fundamental constant related to the effective strength of the electromagnetic force; it’s value is 8.854 × 10−12 C2 m−1J. The letter e indicates the elementary charge; it is the charge on the proton, and the absolute value of the charge on the electron. It’s value is 1.602 × 10−19C, where C is “Coulombs”, the SI unit of charge. Finally, r indicates the distance between the electron and the proton. If we consider the proton to be at the origin, then r=√x2+y2+z2, with (x,y,z) indicating the position of the electron. The Schrödinger equation for an electron in a Hydrogen atom is then:
ˆKψ(→r)−14πϵ0e2rψ(→r)=Eψ(→r)
Here, we’ve written ψ(→r) as a shorthand for ψ(x,y,z); the vector form of r,→r, indicates that the wave function depends on the electron’s displacement from the origin. In fact, it’s more common and more practical to express the wave function in terms of spherical coordinates (r \theta, \phi), where r is the distance from the origin, θ is the angle off of the z axis, and ϕ is the angle off of the x axis in a projection on to the x−y plane. (Even though the potential is spherically symmetric, in that it only depends on the distance from the origin, it turns out that the wave function solution is not always spherically symmetric. The reason for this is angular momentum, and that will be discussed in the next section.)
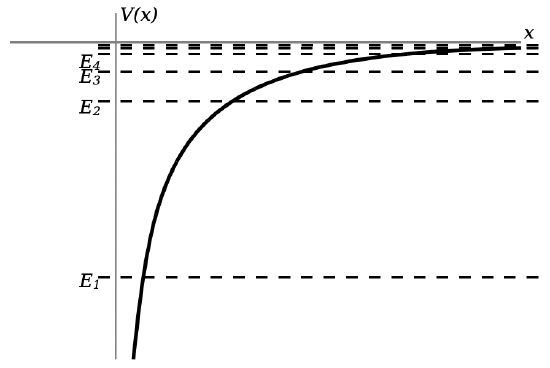
As with the other potentials discussed above, the allowed energy levels are quantized. In the Hydrogen atom, that energy level is specified by a principle quantum number n. The energy levels in a Hydrogen atom are:
En=−13.6eVn2
The ground state of Hydrogen has an energy of −13.6 eV. That is, if you want to tear the electron off of the Hydrogen atom (a process known as ionization), you need to somehow provide at least 13.6 eV of energy in order to give the electron enough energy to make it out to extremely large distances away from the proton.
The figure below slows the Hydrogen atom potential and the first few energy levels. Higher and higher energy levels are less tightly bound (it takes less energy to ionize the atom, freeing the electron). They also get closer and closer together.
In fact, there are three quantum numbers associated with the solution to the Hydrogen atom. In addition to the principle quantum number n, there is also the total orbital angular momentum quantum number l, and the orbital z-angular momentum quantum number m. You could notate the energy eigenstates in a Hydrogen atom, corresponding to a state that the electron could actually be in, by |n,l,m⟩. The ground state for a Hydrogen atom, in this notation, would be |1,0,0⟩. For actual electrons, there’s a fourth quantum number you have to specify: s, the z-spin of the electron. For every state n,l,m in a Hydrogen atom, there are in fact two different electron states, one where the electron has z-spin +ℏ/2, one where the electron has z-spin −ℏ/2. We’ll call this quantum number s, and it will have either the value +1/2 or −1/2.
In Hydrogen, to very good approximation the energy of an eigenstate |n,l,m⟩ only depends on the principal quantum number n, regardless of l and m. That is, the eigenvalue associated with states |2,1,0⟩ and |2,0,0⟩ are exactly the same (and are equal to E=(−13.6eV)/n2=−3.4eV). In atoms with more than one electron, things get more complicated, and the energy of a given state may depend on the other quantum numbers.


