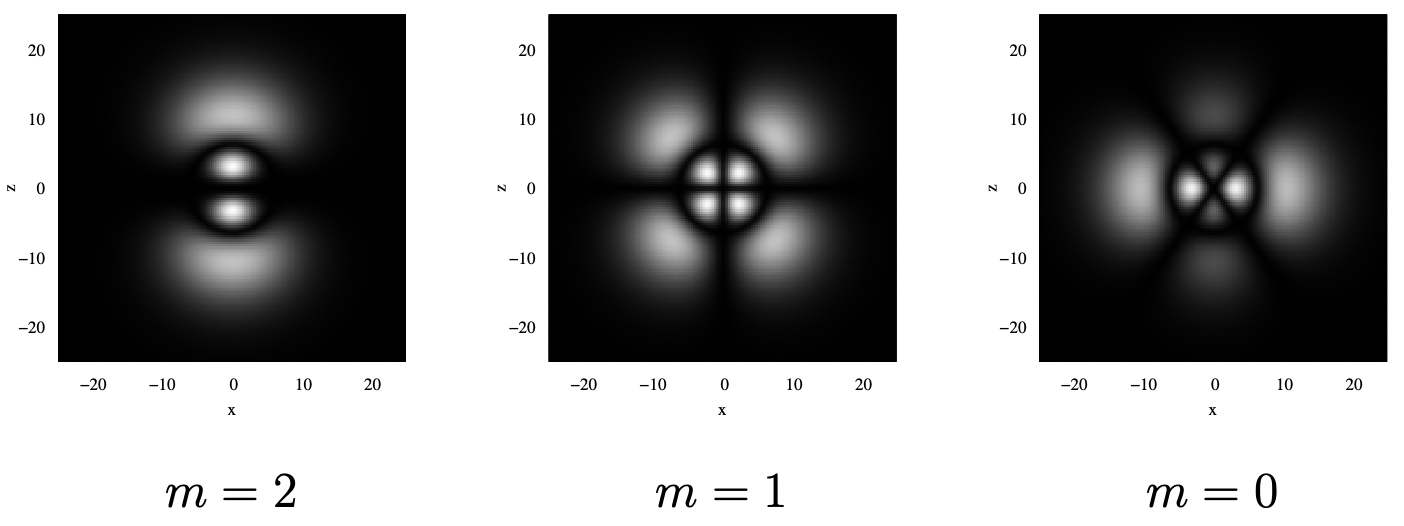
14.3.3: d Orbitals
- Page ID
- 56941
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
When \(l = 2\), the orbitals that are the solutions of the Hydrogen atom Schrödinger equation are called \(d\) orbitals. These orbitals only exist for shells with \(n = 3\) and greater, again because \(l\) must be less than \(n\). As we saw with the \(p\) orbitals, the probability density for the electron in space is the same for \(+m\) and \(−m\). As such, we’ll only plot the positive-\(m\) versions of the orbitals. As before, in addition to a 3d plot showing “shells” at a constant probability level, there is a 2d plot showing a cut in the \(x-z\) plane.
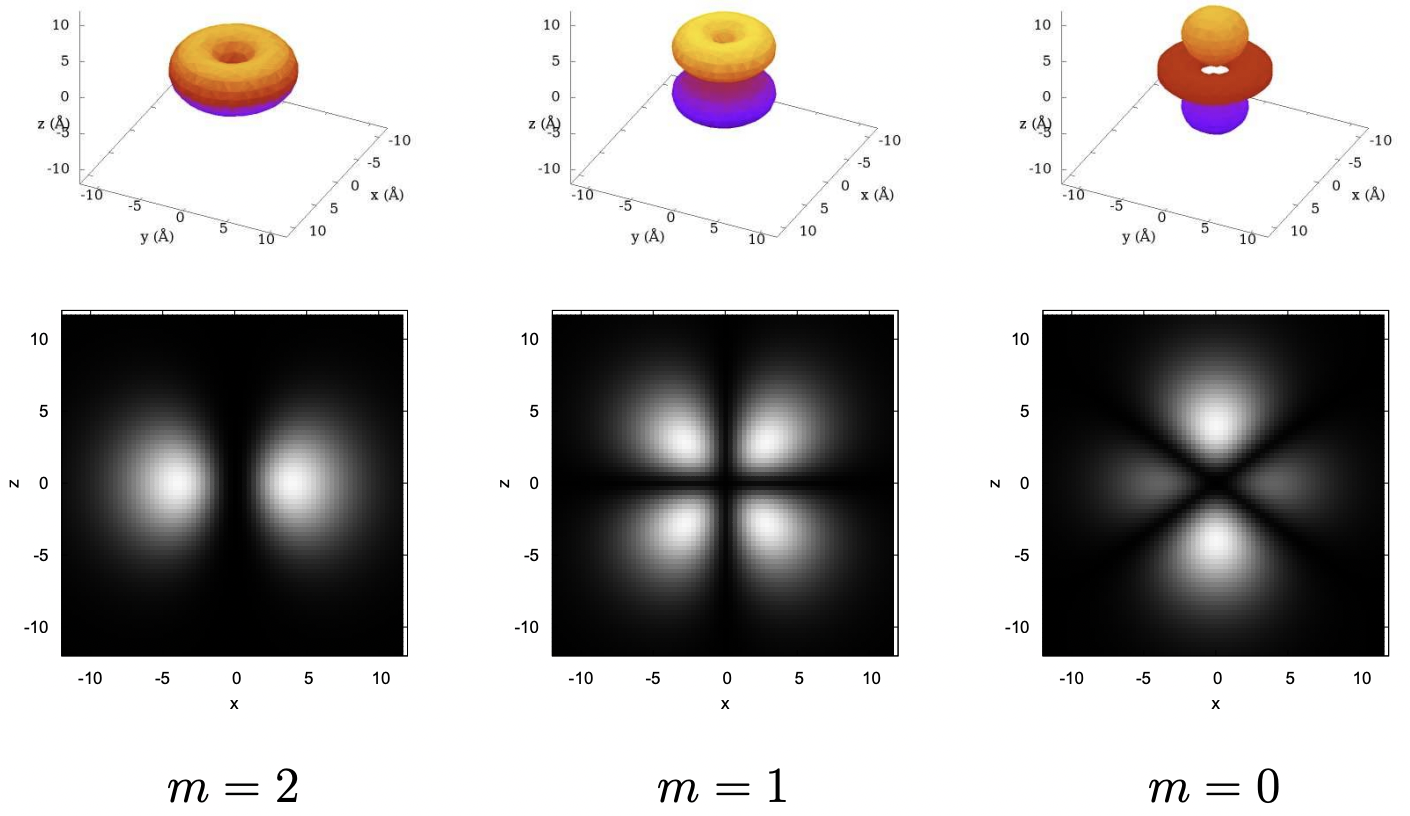
As with the \(p\) orbitals, as we go to the \(d\) orbitals in higher shells they get more interesting. Plotted below are the cuts through the \(x-z\) plane for the \(4d\) orbitals:
