2.2: Plane-Waves
( \newcommand{\kernel}{\mathrm{null}\,}\)
As we have just seen, a wave of amplitude A, wavenumber k, angular frequency ω, and phase angle φ, propagating in the positive x-direction, is represented by the following wavefunction:
ψ(x,t)=Acos(kx−ωt+φ). This type of wave is conventionally termed a one-dimensional plane-wave. It is one-dimensional because its associated wavefunction only depends on the single Cartesian coordinate, x. Furthermore, it is a plane-wave because the wave maxima, which are located at
kx−ωt+φ=j2π, where j is an integer, consist of a series of parallel planes, normal to the x-axis, that are equally spaced a distance λ=2π/k apart, and propagate along the positive x-axis at the velocity v=ω/k. These conclusions follow because Equation (2.2.2) can be rewritten in the form
x=d, where d=(j−φ/2π)λ+vt. Moreover, as is well known, Equation (2.2.3) is the equation of a plane, normal to the x-axis, whose distance of closest approach to the origin is d.
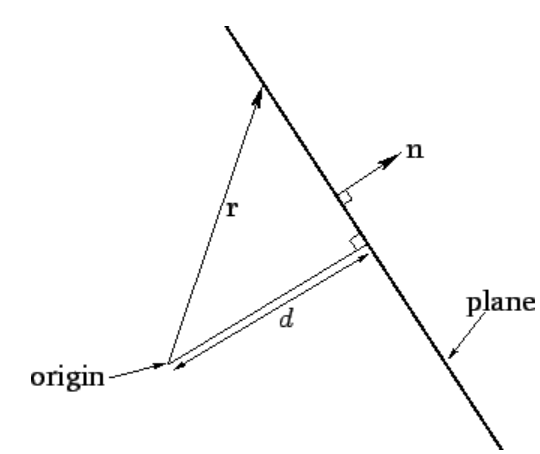
Figure 1: The solution of n⋅r=d is a plane.
The previous equation can also be written in the coordinate-free form
n⋅r=d, where n=(1,0,0) is a unit vector directed along the positive x-axis, and r=(x,y,z) represents the vector displacement of a general point from the origin. Because there is nothing special about the x-direction, it follows that if n is reinterpreted as a unit vector pointing in an arbitrary direction then Equation (2.2.4) can be reinterpreted as the general equation of a plane. As before, the plane is normal to n, and its distance of closest approach to the origin is d. See Figure [f10.1]. This observation allows us to write the three-dimensional equivalent to the wavefunction (2.2.1) as
where the constant vector k=(kx,ky,kz)=kn is called the wavevector. The wave represented previously is conventionally termed a three-dimensional plane-wave. It is three-dimensional because its wavefunction, ψ(r,t), depends on all three Cartesian coordinates. Moreover, it is a plane-wave because the wave maxima are located at k⋅r−ωt+φ=j2π, or n⋅r=(j−φ/2π)λ+vt, where λ=2π/k, and v=ω/k. Note that the wavenumber, k, is the magnitude of the wavevector, k: that is, k≡|k|. It follows, by comparison with Equation (2.2.4), that the wave maxima consist of a series of parallel planes, normal to the wavevector, that are equally spaced a distance λ apart, and that propagate in the k-direction at the velocity v. See Figure [f10.2]. Hence, the direction of the wavevector specifies the wave propagation direction, whereas its magnitude determines the wavenumber, k, and, thus, the wavelength, λ=2π/k.
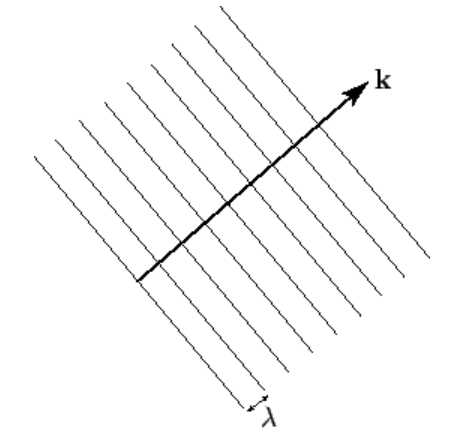
Figure 2: Wave maxima associated with a three-dimensional plane wave.
Contributors and Attributions
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)


