2.2: Plane-Waves

As we have just seen, a wave of amplitude \(A\), wavenumber \(k\), angular frequency \(\omega\), and phase angle \(\varphi\), propagating in the positive \(x\)-direction, is represented by the following wavefunction:

\[\label{e10.1} \psi(x,t)=A\,\cos(k\,x-\omega\,t+\varphi).\] This type of wave is conventionally termed a one-dimensional plane-wave. It is one-dimensional because its associated wavefunction only depends on the single Cartesian coordinate, \(x\). Furthermore, it is a plane-wave because the wave maxima, which are located at

\[\label{e10.2} k\,x-\omega\,t+\varphi = j\,2\pi,\] where \(j\) is an integer, consist of a series of parallel planes, normal to the \(x\)-axis, that are equally spaced a distance \(\lambda=2\pi/k\) apart, and propagate along the positive \(x\)-axis at the velocity \(v=\omega/k\). These conclusions follow because Equation (2.2.2) can be rewritten in the form

\[\label{e10.3} x= d,\] where \(d=(j-\varphi/2\pi)\,\lambda + v\,t\). Moreover, as is well known, Equation (2.2.3) is the equation of a plane, normal to the \(x\)-axis, whose distance of closest approach to the origin is \(d\).

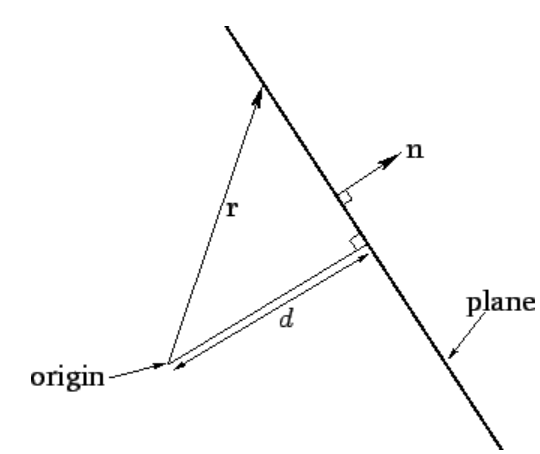
Figure 1: The solution of \(\begin{equation}\mathbf{n} \cdot \mathbf{r}=d\end{equation}\) is a plane. 

The previous equation can also be written in the coordinate-free form

\[\label{e10.4} {\bf n}\cdot{\bf r} = d,\] where \({\bf n} = (1,\,0,\,0)\) is a unit vector directed along the positive \(x\)-axis, and \({\bf r}=(x,\,y,\,z)\) represents the vector displacement of a general point from the origin. Because there is nothing special about the \(x\)-direction, it follows that if \({\bf n}\) is reinterpreted as a unit vector pointing in an arbitrary direction then Equation (2.2.4) can be reinterpreted as the general equation of a plane. As before, the plane is normal to \({\bf n}\), and its distance of closest approach to the origin is \(d\). See Figure [f10.1]. This observation allows us to write the three-dimensional equivalent to the wavefunction (2.2.1) as

\[\label{e10.5} \psi({\bf r},t)=A\,\cos({\bf k}\cdot{\bf r}-\omega\,t+\varphi),\]

where the constant vector \({\bf k} = (k_x,\,k_y,\,k_z)=k\,{\bf n}\) is called the wavevector. The wave represented previously is conventionally termed a three-dimensional plane-wave. It is three-dimensional because its wavefunction, \(\psi({\bf r},t)\), depends on all three Cartesian coordinates. Moreover, it is a plane-wave because the wave maxima are located at \[{\bf k}\cdot{\bf r} -\omega\,t +\varphi= j\,2\pi,\] or \[{\bf n}\cdot{\bf r} = (j-\varphi/2\pi)\,\lambda + v\,t,\] where \(\lambda=2\pi/k\), and \(v=\omega/k\). Note that the wavenumber, \(k\), is the magnitude of the wavevector, \({\bf k}\): that is, \(k\equiv |{\bf k}|\). It follows, by comparison with Equation (2.2.4), that the wave maxima consist of a series of parallel planes, normal to the wavevector, that are equally spaced a distance \(\lambda\) apart, and that propagate in the \({\bf k}\)-direction at the velocity \(v\). See Figure [f10.2]. Hence, the direction of the wavevector specifies the wave propagation direction, whereas its magnitude determines the wavenumber, \(k\), and, thus, the wavelength, \(\lambda=2\pi/k\).

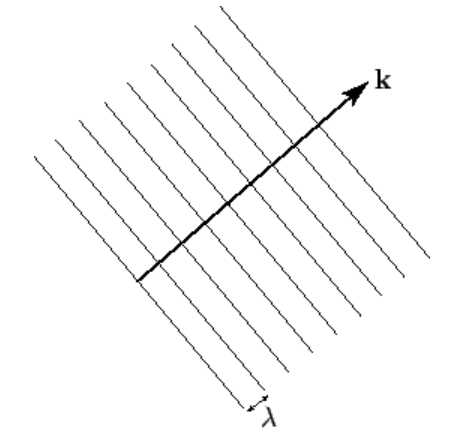
Figure 2: Wave maxima associated with a three-dimensional plane wave.

Contributors and Attributions

• Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

  \( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)