2.3: Representation of Waves via Complex Functions

In mathematics, the symbol \({\rm i}\) is conventionally used to represent the square-root of minus one: in other words, one of the solutions of \({\rm i}^{\,2} = -1\). Now, a real number, \(x\) (say), can take any value in a continuum of different values lying between \(-\infty\) and \(+\infty\). On the other hand, an imaginary number takes the general form \({\rm i}\,y\), where \(y\) is a real number. It follows that the square of a real number is a positive real number, whereas the square of an imaginary number is a negative real number. In addition, a general complex number is written \[z = x + {\rm i}\,y,\] where \(x\) and \(y\) are real numbers. In fact, \(x\) is termed the real part of \(z\), and \(y\) the imaginary part of \(z\). This is written mathematically as \(x={\rm Re}(z)\) and \(y={\rm Im}(z)\). Finally, the complex conjugate of \(z\) is defined \(z^\ast = x-{\rm i}\,y\).

Just as we can visualize a real number as a point lying on an infinite straight-line, we can visualize a complex number as a point lying in an infinite plane. The coordinates of the point in question are the real and imaginary parts of the number: that is, \(z\equiv (x,\,y)\). This idea is illustrated in Figure [f13.2]. The distance, \(r=(x^{\,2}+y^{\,2})^{1/2}\), of the representative point from the origin is termed the modulus of the corresponding complex number, \(z\). This is written mathematically as \(|z|=(x^{\,2}+y^{\,2})^{1/2}\). Incidentally, it follows that \(z\,z^\ast = x^{\,2} + y^{\,2}=|z|^{\,2}\). The angle, \(\theta=\tan^{-1}(y/x)\), that the straight-line joining the representative point to the origin subtends with the real axis is termed the argument of the corresponding complex number, \(z\). This is written mathematically as \({\rm arg}(z)=\tan^{-1}(y/x)\). It follows from standard trigonometry that \(x=r\,\cos\theta\), and \(y=r\,\sin\theta\). Hence, \(z= r\,\cos\theta+ {\rm i}\,r\sin\theta\).

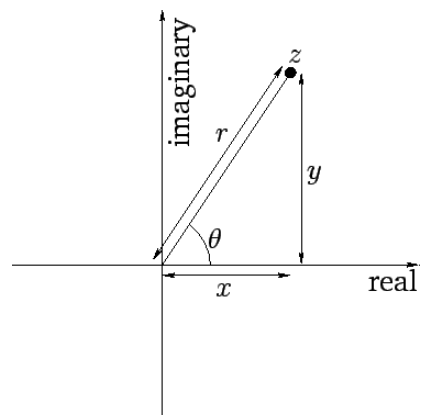
Figure 3: Representation of a complex number as a point in a plane.

Complex numbers are often used to represent wavefunctions. All such representations depend ultimately on a fundamental mathematical identity, known as Euler’s theorem , that takes the form \[{\rm e}^{\,{\rm i}\,\phi} \equiv \cos\phi + {\rm i}\,\sin\phi,\] where \(\phi\) is a real number. Incidentally, given that \(z=r\,\cos\theta + {\rm i}\,r\,\sin\theta= r\,(\cos\theta+{\rm i}\,\sin\theta)\), where \(z\) is a general complex number, \(r=|z|\) its modulus, and \(\theta={\rm arg}(z)\) its argument, it follows from Euler’s theorem that any complex number, \(z\), can be written \[z = r\,{\rm e}^{\,{\rm i}\,\theta},\] where \(r=|z|\) and \(\theta={\rm arg}(z)\) are real numbers.

A one-dimensional wavefunction takes the general form

\[\label{e12.8} \psi(x,t) = A\,\cos(k\,x-\omega\,t+\varphi),\] where \(A\) is the wave amplitude, \(k\) the wavenumber, \(\omega\) the angular frequency, and \(\varphi\) the phase angle. Consider the complex wavefunction

\[\label{e12.10} \psi(x,t) = \psi_0\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)},\] where \(\psi_0\) is a complex constant. We can write \[\psi_0 = A\,{\rm e}^{\,{\rm i}\,\varphi},\] where \(A\) is the modulus, and \(\varphi\) the argument, of \(\psi_0\). Hence, we deduce that \[\begin{aligned} {\rm Re}\left[\psi_0\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)}\right] &= {\rm Re}\left[A\,{\rm e}^{\,{\rm i}\,\varphi}\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)}\right]={\rm Re}\left[A\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t+\varphi)}\right]=A\,{\rm Re}\left[{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t+\varphi)}\right].\end{aligned}\] Thus, it follows from Euler’s theorem, and Equation (2.3.4), that \[{\rm Re}\left[\psi_0\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)}\right] =A\,\cos(k\,x-\omega\,t+\varphi)=\psi(x,t).\] In other words, a general one-dimensional real wavefunction, (2.3.4), can be represented as the real part of a complex wavefunction of the form (2.3.5). For ease of notation, the “take the real part” aspect of the previous expression is usually omitted, and our general one-dimension wavefunction is simply written

\[\label{e12.13} \psi(x,t) = \psi_0\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)}.\] The main advantage of the complex representation, (2.3.8), over the more straightforward real representation, (2.3.4), is that the former enables us to combine the amplitude, \(A\), and the phase angle, \(\varphi\), of the wavefunction into a single complex amplitude, \(\psi_0\). Finally, the three-dimensional generalization of the previous expression is \[\psi({\bf r},t) = \psi_0\,{\rm e}^{\,{\rm i}\,({\bf k}\cdot{\bf r}-\omega\,t)},\] where \({\bf k}\) is the wavevector.

Contributors and Attributions

• Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

  \( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)