4.4: Cold Emission
( \newcommand{\kernel}{\mathrm{null}\,}\)
Suppose that an unheated metal surface is subject to a large uniform external electric field of strength E, which is directed such that it accelerates electrons away from the surface. We have already seen (in Section [s3.3]) that electrons just below the surface of a metal can be regarded as being in a potential well of depth W, where W is called the workfunction of the surface. Adopting a simple one-dimensional treatment of the problem, let the metal lie at x<0, and the surface at x=0. Now, the applied electric field is shielded from the interior of the metal. Hence, the energy, E, say, of an electron just below the surface is unaffected by the field. In the absence of the electric field, the potential barrier just above is the surface is simply V(x)−E=W. The electric field modifies this to V(x)−E=W−eEx. The potential barrier is sketched in Figure [fcold].
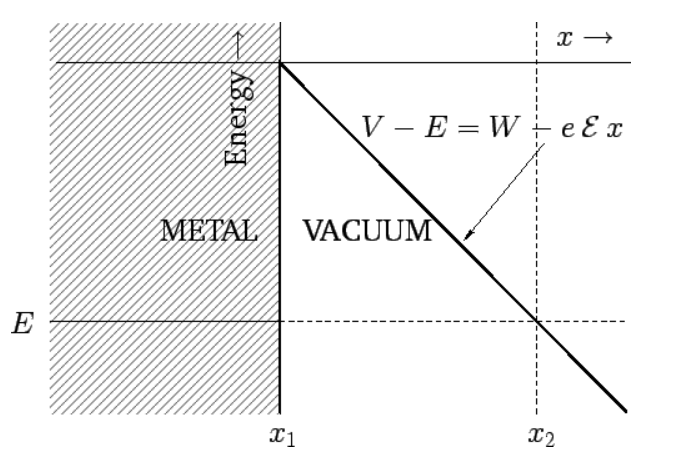
Figure 14: The potential barrier for an electron in a metal surface subject to an external electric field.
It can be seen, from Figure [fcold], that an electron just below the surface of the metal is confined by a triangular potential barrier which extends from x=x1 to x2, where x1=0 and x2=W/eE. Making use of the WKB approximation (see the previous section), the probability of such an electron tunneling through the barrier, and consequently being emitted from the surface, is |T|2=exp(−2√2mℏ∫x2x1√V(x)−Edx),
The cold emission of electrons from a metal surface is the basis of an important device known as a scanning tunneling microscope, or an STM. An STM consists of a very sharp conducting probe which is scanned over the surface of a metal (or any other solid conducting medium). A large voltage difference is applied between the probe and the surface. Now, the surface electric field-strength immediately below the probe tip is proportional to the applied potential difference, and inversely proportional to the spacing between the tip and the surface. Electrons tunneling between the surface and the probe tip give rise to a weak electric current. The magnitude of this current is proportional to the tunneling probability ([e5.53]). It follows that the current is an extremely sensitive function of the surface electric field-strength, and, hence, of the spacing between the tip and the surface (assuming that the potential difference is held constant). An STM can thus be used to construct a very accurate contour map of the surface under investigation. In fact, STMs are capable of achieving sufficient resolution to image individual atoms
Contributors and Attributions
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)


