3.1: 1-D Schrödinger Equation - Example Systems
- Page ID
- 2854
Curvature of Wavefunctions
Schrödinger’s equation in the form \[ \frac{d^2\psi(x)}{dx^2}=\frac{2m(V(x)-E)}{\hbar^2}\psi(x) \label{3.1.1}\]
can be interpreted by saying that the left-hand side, the rate of change of slope, is the curvature – so the curvature of the function is proportional to \((V(x)-E)\psi(x)\). This means that if \(E>V(x)\), for \(\psi(x)\) positive \(\psi(x)\) is curving negatively, for \(\psi(x)\) negative \(\psi(x)\) is curving positively. In both cases, \(\psi(x)\) is always curving towards the x-axis -- so, for \(E>V(x)\), \(\psi(x)\) has a kind of stability: its curvature is always bringing it back towards the axis, and so generating oscillations. The simplest example is that of a constant potential \(V(x)=V_0<E\), for which the wavefunction is
\[\psi(x)=A\sin(kx+\delta) \label{PIB1}\]
with \(\delta\) a constant and
\[k=\sqrt{(2m/\hbar^2)(E−V_0)}.\]
On the other hand, for \(V(x)>E\), the curvature is always away from the axis. This means that \(\psi(x)\) tends to diverge to infinity. Only with exactly the right initial conditions will the curvature be just right to bring the wavefunction to zero as \(x\) goes to infinity. (This is possible because as \(\psi(x)\) tends to zero, the curvature tends to zero, too.)
For a constant potential \(V_0>E\), the wavefunction is
\[\psi(x)=Ae^{\alpha x}+Be^{−\alpha x}\]
with
\[\alpha=\sqrt{(2m/\hbar^2)(V_0−E)}.\]
Of course, this wavefunction will diverge in at least one direction! However, as we shall see below, there are situations with spatially varying potentials where this wavefunction is only relevant for positive \(x\), and the coefficients \(A\), \(B\) are functions of the energy -- for certain energies it turns out that \(A=0\), and the wavefunction converges.
One Dimensional Infinite Depth Square Well
In an earlier lecture, we considered in some detail the allowed wavefunctions and energies for a particle trapped in an infinitely deep square well, that is, between infinitely high walls a distance \(L\) apart. For that case, the potential between the walls is identically zero so the wavefunction has the form (Equation \ref{PIB1}). The wavefunction \(\psi(x)\) necessarily goes to zero right at the walls, since it cannot have a discontinuity, and must be zero just inside the wall. Even a quantum particle cannot penetrate an infinite wall!
An immediate consequence is that the lowest state cannot have zero energy, since \(k=0\) gives a constant \(\psi(x)\). Rather, the lowest energy state must have the minimal amount of bending of the wavefunction necessary for it to be zero at both walls but nonzero in between -- this corresponds to half a period of a sine or cosine (depending on the choice of origin), these functions being the solutions of Schrödinger’s equation in the zero potential region between the walls. The allowed wavefunctions (eigenstates) found as the energy increases have successively 0, 1, 2, … zeros (nodes) in the well.
Parity of a wavefunction
Notice that the allowed wave eigenfunctions of the Hamiltonian for the infinite well are symmetrical or antisymmetrical about the center:
\[\psi(x)=\pm\psi(−x).\]
We call the operator that reflects a function in the origin the parity operator \(P\), so these eigenstates of the Hamiltonian are also eigenstates of the parity operator, with eigenvalues \(\pm 1\). This is because the Hamiltonian is itself symmetric: \(d^2/dx^2\) is even in \(x\), and so is \(V(x)\), so \([H,P]=0\), and the two operators can be simultaneously diagonalized, that is, a common set of eigenstates can be constructed.
Finite Depth Square Well
If the potential at the walls is not infinite, the parity operator \(P\) will continue to commute with the Hamiltonian \(H\) as long as the potential is symmetric, \(V(x)=V(−x)\).
We take
\[ \begin{matrix} V(x)=V_0,& x<−L/2,\\ V(x)=0,& −L/2≤x≤L/2,\\ V(x)=V_0,& L/2<x.\end{matrix} \label{3.1.2}\]
We only need look for solutions symmetric or antisymmetric about the origin. This is important from a practical point of view, because it allows us to integrate Schrödinger’s equation numerically out from the origin in the positive direction: \(\psi(x)\) in the negative direction is fixed by symmetry (or antisymmetry). Since it’s a second-order equation, we need two boundary conditions to get going, for symmetric states, we can take at x=0, for antisymmetric states, \(\psi(x)=0\), \(\psi′(x)=1\) at \(x=0\). (Of course, we will have to normalize \(\psi(x)\) correctly eventually.)
The numerical strategy is to pick a value for the energy \(E\), choose one of the boundary conditions above and integrate \(\psi(x)\) numerically to a large positive value of \(x\). For almost all values of \(E\), the wavefunction will be exponentially increasing with \(x\). For the particular values corresponding to bound states, it will be exponentially decreasing.
It is well worth while building up an intuition for this by playing with the spreadsheet accompanying this lecture: the spreadsheet does the numerical integration for any \(E\) and well depth, and has a macro to locate the nearest bound state.
Joining the wavefunctions Inside and Outside of the Well
The numerical method mentioned above works for any symmetric potential. Fortunately, for the square well, an analytic/graphical method is very effective, and provides more insight.
Let us begin by considering how the lowest energy state wavefunction is affected by having finite instead of infinite walls. Inside the well, where \(V=0\), the solution to Schrödinger’s equation is still of cosine form (for a symmetric state). However, Schrödinger’s equation now has a nonzero solution inside the wall \((x>L/2)\), where \(V=V_0\):
\[−\frac{\hbar^2}{2m}\frac{d^ 2\psi(x)}{d x^2}+V_0\psi(x)=E\psi(x), \label{3.1.3}\]
has two exponential solutions one increasing with \(x\), the other decreasing,
\[ e^{\alpha x}\; and\; e^{−\alpha x} \label{3.1.4}\]
where \(\alpha=\sqrt{2m(V_0−E)/\hbar^2}.\) We are assuming here that \(E<V_0\), so the particle is bound to the well. We shall find the lowest energy state is always bound in a finite square well, however weak the potential.
Now, Schrödinger’s equation must be valid everywhere, including the point \(x=L/2\). Since the potential is finite, the wavefunction \(\psi(x)\) and its first derivative must be continuous at \(x=L/2\).
Suppose, then, we choose a particular energy \(E\). Then the wavefunction inside the well (taking the symmetric case) is proportional to coskx, where \(k=\sqrt{2mE/\hbar^2}\). The wavefunction (and its derivative!) must match a sum of exponential terms at \(x=L/2\), so
\[ \begin{matrix} \cos(kL/2)=Ae^{\alpha L/2}+Be^{−\alpha L/2}\\ −k\sin(kL/2)=\alpha Ae^{\alpha L/2}−\alpha Be^{−\alpha L/2} \end{matrix} \label{3.1.5}\]
Solving these equations for the coefficients \(A\), \(B\) in the usual way, we find that in general the cosine solution inside the well goes smoothly into a linear combination of exponentially increasing and decreasing terms in the wall. However, this cannot in general represent a bound state in the well. The increasing solution increases without limit as \(x\) goes to infinity, so since the square of the wavefunction is proportional to the probability of finding the particle at any point, the particle is infinitely more likely to be found at infinity than anywhere else. It got away! This clearly makes no sense -- we’re trying to find wavefunctions for particles that stay in, or at least close to, the well. We are forced to conclude that the only exponential wavefunction that makes sense is the one for which \(A\) is exactly zero, so that there is only a decreasing wave in the wall.
Finding the Bound State Energies Graphically
If we demand that the wavefunction decrease exponentially as \(x\) goes to infinity, or, in other words, require A to be zero, \(k\) must satisfy the condition given be dividing one of the boundary equations above by the other:
\[ \tan(kL/2)=\alpha/k. \label{3.1.6}\]
This equation cannot be solved analytically, but is easy to solve graphically by plotting the two sides as functions of \(k\) (recall \(\alpha=\sqrt{2m(V_0−E)/\hbar^2}\), and \(k=\sqrt{2mE/\hbar^2}\)) and finding where the curves intersect.
From \[ \alpha^2=\frac{2mV_0}{\hbar^2}−k^2 \;\; we\; find \;\; \frac{\alpha}{k}=\sqrt{\frac{2mV_0}{\hbar^2k^2}−1} \label{3.1.7}\]
note that this is real only for \[ k<\frac{\sqrt{2mV_0}}{\hbar}. \label{3.1.8}\]
(Because if this inequality is not satisfied, the particle has enough kinetic energy to get out of the well!)
Now the condition for a bound state can be written
\[ \tan(kL/2)=\frac{\alpha}{k}=\sqrt{\frac{2mV_0}{\hbar^2k^2}−1} \label{3.1.9}\]
Cleaning up the appearance of the equation by choosing variables \(x=\frac{kL}{2}\), \(a^2=\frac{mV_0L^2}{2\hbar^2}\), and plotting \(\tan x\) and \(\sqrt{(\frac{a}{x})^2−1}\) from \(x=0\) to \(x=a\) allowed bound state \(k\)-values correspond to the points of intersection of the two curves. The bound state energies are then given by \(E=\hbar^2k^2/2m\).
The variable \(a\) is a measure of the attractive strength of the well. Here are the two curves for a shallow well ( \(a=1\) ):
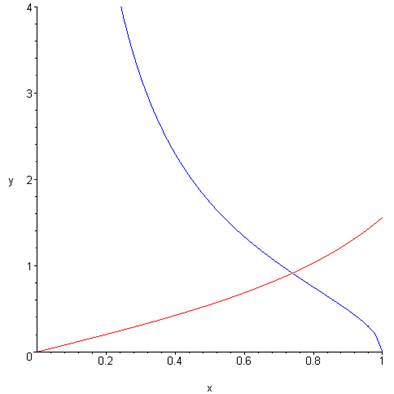
It is interesting to note that however small \(a\) is, the curve \(y=\sqrt{(\frac{a}{x})^2−1}\) goes to infinity as \(x\) goes to zero, so will always intersect \(y=\tan x\): there will always be a bound state.
A deeper well, \(a=20\), gives several bound states:
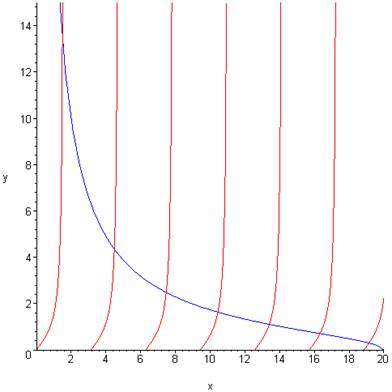
For the lower energies at least, the allowed \(k\)–values are approximately linearly spaced, at about \(\pi/2\), \(3\pi/2\), \(5\pi/2\),… so the bound state energies are not far off the 1, 9, 25,… pattern of the infinitely deep square well -- remembering that we are only looking at the even parity (cosine) solutions!
Exercise \(\PageIndex{1}\)
Use the spreadsheet with D = 50, W = 4 and find all the even bound state energies. How well do they fit this pattern? Can you account for the deviation? Examine the wavefunctions for the different eigenenergies: note how far it penetrates the wall, and how much that changes the boundary condition at the wall from that for an infinite wall. Which one of the bound state energies is most affected by this, and how is it affected? Would you expect that from the graphical solution?
The odd parity solutions, sine waves inside the well, can be found by an exactly similar analysis. One difference is that an arbitrarily weak well will not bind an odd parity state. The point is that for a weak potential to bind an even state, it only has to curve the wavefunction slightly to get from one exponentially decaying to the left to one exponentially decaying to the right. These curves decay very slowly for a weak potential, and give a bound state in which the particle is most likely to be found outside the well. On the other hand, in an odd solution the wavefunction within the well has to have enough total curvature to fit together two decaying wavefunctions which have opposite sign. This takes much more bending, and cannot be achieved with a very weak potential.
Exercise \(\PageIndex{2}\)
Check this last statement, by considering what fraction of a wavelength of the oscillating wavefunction inside the well is necessary to make a connection between the decaying wavefunctions in the walls to the left and right.
The Delta Function Potential
One limiting case of a square well is a very narrow deep well, which can be approximated by a delta function when the range of variation of the wavefunction is much greater than the range of the potential, so Schrödinger’s equation becomes \[-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}+\lambda\delta(x)\psi(x)=E\psi(x) \label{3.1.10}\]
with \(\lambda\) negative for an attractive potential.
The infinity of the \(\delta\)-function cannot be balanced by the finite right hand side, so the wavefunction must have a discontinuity in slope at the origin.
To find the ground state energy, note first that as a one-dimensional attractive potential there will be a bound state: any change in slope is sufficient to connect an exponentially increasing function coming in from \(−\infty\) to a decreasing one going to \(+\infty\), since the rates of increase and decrease can be arbitrarily slow.
Away from the origin, then, we can take the wavefunction to be \[ \psi(x)=Ae^{−\alpha|x|}, \label{3.1.11}\]
the energy of the state being \(E=−\hbar^2\alpha^2/2m\).
The discontinuity in slope at the origin is just \[ \frac{d\psi(x=+\varepsilon)}{dx}−\frac{d\psi(x=−\varepsilon)}{dx}=−2A\alpha.\label{3.1.12}\]
To match this with the \(\delta\)-function singularity, we integrate the Schrödinger equation term by term from \(−\varepsilon\) to \(+\varepsilon\) in the limit of \(\varepsilon\) going to zero:
\[ \int_{-\varepsilon}^{\varepsilon}-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}dx+\int_{-\varepsilon}^{\varepsilon}\lambda \delta(x)\psi(x)dx=\int_{-\varepsilon}^{\varepsilon}E\psi(x)dx. \label{3.1.13}\]
Note first that the right-hand side, having a finite integrand, must go to zero in the limit of \(\varepsilon\) going to zero.
The \(\delta\)-function term must integrate to \(\lambda\psi(0)=\lambda A\).
The first term just gives the discontinuity in slope,
\[ \int_{-\varepsilon}^{\varepsilon}-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}dx=-\frac{\hbar^2}{2m}\int_{-\varepsilon}^{\varepsilon}\frac{d}{dx}\left( \frac{d\psi}{dx}\right) dx=−\frac{\hbar^2}{2m}\left[ \frac{d\psi}{dx}\right]^{\varepsilon}_{−\varepsilon}=\frac{\hbar^2}{2m}2A\alpha. \label{3.1.14}\]
Schrödinger’s equation is therefore satisfied if \(\hbar^2\alpha/m+\lambda =0\) (remembering \(\lambda\) is negative for an attractive potential).
The energy of the bound state is \[ E=−\frac{\hbar^2\alpha^2}{2m}=−\frac{m\lambda^2}{2\hbar^2}.\label{3.1.15}\]
Exercise \(\PageIndex{1}\)
Rederive this result by taking the limit of a narrow deep well, tending to a \(\delta\)-function, with a cosine wavefunction inside.
A Potential Step
Our analysis so far has been limited to real-valued solutions of the time-independent Schrödinger equation. This is fine for analyzing bound states in a potential, or standing waves in general, but cannot be used, for example, to represent an electron traveling through space after being emitted by an electron gun, such as in an old fashioned TV tube. The reason is that a real-valued wavefunction \(\psi(x)\), in an energetically allowed region, is made up of terms locally like \(\cos kx\) and \(\sin kx\), multiplied in the full wavefunction by the time dependent phase factor \(e^{-iEt/\hbar}\), giving equal amplitudes of right moving waves \(e^{i(px−Et)/\hbar}\) and left moving waves \(e^{−i(px+Et)/\hbar}\). So, for an electron definitely moving to the right, even the time-independent part of the wavefunction must necessarily be complex.
Consider an electron of energy \(E\) moving in one dimension through a region of zero potential from large negative \(x\) and encountering an upward step potential of height \(V_0\) ( \(V_0<E\) ) at the origin \(x=0\). Of course, strictly speaking, the electron should be represented by a wave packet, and hence could not have a precisely defined energy \(E\), but we assume here that it is a very long wave packet, very close to a plane wave, so we take it that the wavefunction is: \[ \psi(x,t)=Ae^{ikx}e^{-iEt/\hbar}\;\; for\;\; x< 0 \label{3.1.16}\]
(A more precise analysis, in which an incoming wave packet is used, can be done by solving for the plane-wave components individually. In the limit of a wavepacket long compared to the de Broglie wavelength, the result is the same as that found here.)
Visualizing the classical picture of a particle approaching a hill (smoothing off the corners a bit) that it definitely has enough energy to surmount, we would perhaps expect that the wavefunction continues beyond \(x=0\) in the form \[ \psi(x,t)=Be^{ik_1x}e^{-iEt/\hbar}\;\; for\;\; x>0,\label{3.1.17}\]
where \(k_1\) corresponds to the slower speed the particle will have after climbing the hill.
Schrödinger’s equation requires that the wavefunction have no discontinuities and no kinks (discontinuities in slope) so the \(x<0\) and \(x>0\) wavefunctions must match smoothly at the origin. For them to have the same value, we see from above that \(A=B\). For them to have the same slope we must have \(kA=k_1B\). Unfortunately, the only way to satisfy both these equations with our above wavefunctions is to take \(k=k_1\) -- which means there is no step potential at all!
Example \(\PageIndex{1}\)
What is wrong with the above reasoning?
Solution?
The answer is that we have been led astray by the depiction of the particles as little balls rolling along in a potential, with enough energy to get up the hill, etc. Schrödinger’s equation is a wave equation. Building intuition about solutions should rely on experience with waves. We should be thinking about a light wave going from air into glass, for example. If we do, we realize that at any interface some of the light gets reflected. This means that our expression for the wavefunction for \(x<0\) is incomplete, we need to add a reflected wave, giving
\[ \begin{matrix}\psi(x,t)=Ae^{ikx}e^{-iEt/\hbar} +Ce^{-ikx}e^{-iEt/\hbar}& for& x<0,\\ \psi(x,t)=Be^{ik_1x}e^{-iEt/\hbar} & for& x>0. \end{matrix} \label{3.1.18}\]
Now matching the wavefunction and its derivative at the origin, \[ \begin{matrix} A+C=B\\ k(A−C)=k_1B.\end{matrix} \label{3.1.19}\]
The fraction of the wave that is reflected \[ R=\frac{C^2}{A^2}=\left( \frac{k−k_1}{k+k_1}\right)^2. \label{3.1.20}\]
Evidently, the fraction of the wave transmitted \[ T=1−R=\frac{4kk_1}{(k+k_1)^2} .\label{3.1.21}\]
Example \(\PageIndex{2}\)
Isn’t the amount transmitted just given by \(B^2/A^2\)?
Solution?
The answer is no. The ratio \(B^2/A^2\) gives the relative probability of finding a particle in some small region in the transmitted stream relative to that in the incoming stream, but the particles in the transmitted stream are moving more slowly, by a factor \(k_1/k\). That means that just comparing the densities of particles in the transmitted and incoming streams is not enough. The physically significant quantity is the probability current flowing past a given point, and this is the product of the density and the speed. Therefore, the transmission coefficient is \(B^2k_1/A^2k\).
Exercise \(\PageIndex{1}\)
Prove that even a step down gives rise to some reflection.
Tunneling through a Square Barrier
If a plane wave coming in from the left encounters a step at the origin of height \(V_0>E\), the incoming energy, there will be total reflection, but with an exponentially decaying wave penetrating some distance into the step. This, by the way, is a general wave phenomenon, not confined to quantum mechanics. If a light wave traveling through a piece of glass is totally internally at the surface, there will be an exponentially decaying electromagnetic field in the air outside the surface. If another piece of glass with a parallel (flat) surface is brought close, some light will “tunnel through” the air gap into the second piece of glass. We are considering here the quantum analogue of this classical behavior.
Suppose then we replace the step with a barrier, \[ \begin{matrix} V=0& for& x<0,& call\; this\; region\; I\\ V=V_0& for& 0<x<L,& this\; is\; region\; II\\ V=0& for& L<x,& region\; III.\end{matrix}\label{3.1.22}\]
In this situation, the wavefunction will still decay exponentially into the barrier (assuming the barrier is thick compared to the exponential decay length), but on reaching the far end at \(x=L\), a plane wave solution is again allowed, so there is a nonzero probability of finding the particle beyond the barrier, moving with its original speed. This phenomenon is called tunneling, since in the classical (particle) picture the particle doesn’t have enough energy to get over the top of the barrier.
The way to solve the problem is to solve the Schrödinger equation in the three regions, then apply the boundary conditions. Since we are interested in the probability of a particle getting through the barrier, we do not need to worry about normalizing the wavefunction, so for simplicity we take an incoming wave of unit amplitude. In region I, there will also be a reflected wave, so \[ \psi_I(x)=e^{ikx}+Be^{-ikx}. \label{3.1.23}\]
In region II, there will in general be both exponentially decreasing and exponentially growing solutions, so we take \[ \psi_{II}(x)=Ce^{\alpha x}+De^{-\alpha x}. \label{3.1.24}\]
Recall \(\alpha=\sqrt{(2m/\hbar^2)(V_0-E)}\)
In region III, there is only the outgoing wave, to make the equations easy we absorb a phase factor in the coefficient, and write: \[ \psi_{III}(x)=Se^{ik(x-L)}.\label{3.1.25}\]
We now require \(\psi(x)\) and \(\psi′(x)\) be continuous at \(x=0\), \(L\). Elementary computations lead to \[ \begin{matrix}2ik=(ik+\alpha)C+(ik-\alpha)D\\ 2\alpha Ce^{\alpha L}=(ik+\alpha)S\\ 2\alpha De^{-\alpha L}=-(ik-\alpha)S. \end{matrix}\label{3.1.26}\]
Solving these equations gives \[ S(k)=\frac{2k\alpha}{2k\alpha\cosh\alpha L+i(\alpha^2-k^2)\sinh\alpha L}. \label{3.1.27}\]
The probability of tunneling is: \[ |S(k)|^2=\frac{4k^2\alpha^2}{(k^2+\alpha^2)^2\sinh^2\alpha L+4k^2\alpha^2}. \label{3.1.28}\]
An important limit is that of a barrier thick compared with the decay length, \(\alpha L\gg1\).
In this limit, \(\sinh^2\alpha L\approx \frac{1}{4}e^{2\alpha L}\), and using \(\alpha=\sqrt{(2m/\hbar^2)(V_0-E)}\), \(E=\hbar^2k^2/2m\), we find \[ |S(k)|^2\cong 16\left( \frac{E}{V_0}\right) \left( 1-\frac{E}{V_0}\right) e^{-2\alpha L}.\label{3.1.29}\]
In typical tunneling problems, the far and away dominant term is the \(e^{-2\alpha L}\), which may differ from unity by many orders of magnitude.
The Spherically Symmetric Three-Dimensional Problem
The methods developed above for the one-dimensional system are almost immediately applicable to a very important three-dimensional case: a particle in a spherically symmetric potential. A more detailed treatment will be given later -- we restrict ourselves here to spherically symmetric solutions of Schrödinger’s equation \(\psi(r,\theta,\phi)=\psi(r)\), a subspace of the space of all possible solutions that always includes the ground state.
The kinetic energy operator on states in this subspace (where \(d/d\theta\equiv 0\), \(d/d\phi\equiv 0\) ) is \[ \frac{\vec{p}^2}{2m}=−\frac{\hbar^2\vec{\nabla}^2}{2m}=-\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{d}{dr}(r^2\frac{d}{dr}). \label{3.1.30}\]
It is easy to check that if we write the wavefunction \[ \psi(r)=\frac{u(r)}{r} \label{3.1.31}\]
the function \(u(r)\) obeys the one-dimensional equation \[ -\frac{\hbar^2}{2m}\frac{d^2u(r)}{dr^2}+V(r)u(r)=Eu(r) \label{3.1.32}\]
exactly like a particle in one dimension, except that here \(r\) is only positive, and \(u(r)\) must go to zero at the origin. (If \(u(r)\) does not go to zero, \(\psi(r)\) will be at best of order \(1/r\) near the origin, and, going back momentarily to three dimensions, \(\vec{\nabla}^2\psi\sim \delta(\vec{r})\), so Schrödinger’s equation will not be satisfied with any realizable potential.)
Exercise: for a spherical square well, \(V=0\) if \(r<r_0\), \(V=V_0\) for \(r\ge r_0\), find the minimum value of \(V_0\) for which a bound state exists for given \(r_0\) and particle mass \(m\). Sketch the wavefunction.
Alpha Decay
A good example of tunneling, and one which historically helped establish the validity of quantum ideas at the nuclear level, is \(\alpha\)-decay. Certain large unstable nuclei decay radioactively by emitting an \(\alpha\)-particle, a tightly bound state of two protons and two neutrons. It is thought that \(\alpha\)-particles may exist, at least as long lived resonances, inside the nucleus. For such a particle, the strong but short ranged nuclear force creates a spherical finite depth well having a steep wall more or less coinciding with the surface of the nucleus. However, we must also include the electrostatic repulsion between the \(\alpha\)-particle and the rest of the nucleus, a potential \((1/4\pi\varepsilon_0)(Z-2)2e^2/r\) outside the nucleus. This means that, as seen from inside the nucleus, the wall at the surface may not be a step but a barrier, in the sense we used the word above, a step up followed by a slide down the electrostatic curve:
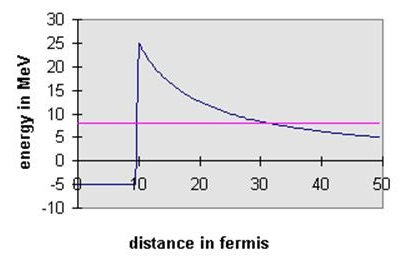
Therefore, an \(\alpha\)-particle bouncing around inside the nucleus may have enough energy to tunnel through to the outside world.
The \(\alpha\)-particles are emitted with spherical symmetry, so the wavefunction can be written \(\psi(r)=u(r)/r\), as discussed above, and Schrödinger’s equation is \[ -\frac{\hbar^2}{2m}\frac{d^2u(r)}{dr^2}+V(r)u(r)=Eu(r), \;\; r>0 \label{3.1.33}\]
It is evident that the more energetic the \(\alpha\)-particle is, the thinner the barrier it faces. Since the wavefunction decays exponentially in the barrier, this can make a huge difference in tunneling rates. It is not difficult to find the energy with which the \(\alpha\)-particle hits the nuclear wall, because this will be the same energy with which it escapes. Therefore, if we measure the energy of an emitted \(\alpha\), since we think we know the shape of the barrier pretty well, we should be able, at least numerically, to predict the tunneling rate. The only other thing we need to know is how many times per second \(\alpha\)’s bounce off the wall. The size of the nucleus is of order \(10^{-14}\) meters (10 fermis), if we assume an \(\alpha\) moves at, say, \(10^{7}\) meters per second, it will bang into the wall \(10^{21}\) times per second. This is a bit handwaving, but all \(\alpha\)-radioactive nuclei are pretty much the same size, so perhaps it’s safe to assume this will be about the same for all of them.
This is a huge number -- the probability of transmission is evidently very tiny! In other words, the decay length of the wavefunction inside the barrier is extremely short (except for the very last bit as it emerges into the outside world). It’s so short, in fact, that we can get results in good agreement with experiment by dividing the barrier into a sequence of square barriers and using the above \(\alpha L\gg 1\) formula for each of them, \[ \psi(r+\Delta r)\approx \psi(r)e^{-\alpha(r)\delta r} \label{3.1.34}\]
(neglecting the slowly varying and completely unimportant \(1/r\) term) so the total attenuation of the wavefunction in this approximation is the product of terms like this, \[ \begin{matrix} \psi(exit)=\psi(nucl)\prod_i e^{-\alpha(r_i)\Delta r}\\ \approx \psi(nucl)e^{-\int \alpha(r)dr}\\ =\psi(nucl)e^{-\int \sqrt{(2m/\hbar^2)V(r)-E} dr} \end{matrix} \label{3.1.35}\]
Since we know the actual shape of the barrier, this integral can be done with elementary functions, and the result for the transmission rate is
\[ |S(k)|^2\approx Ae^{-B/\sqrt{E}}. \label{3.1.36}\]
Here \(B=(\pi\sqrt{2m}/\hbar )(Z-2)2e^2\) is not an adjustable parameter: and plotting \(\ln|S(k)|^2\) against \(1/\sqrt{E}\) for Polonium212 (which emits \(\alpha\)’s with energy 8.95MeV, and lasts \(3\times 10^{-7}\) seconds) Thorium232 (4.05MeV \(\alpha\)’s, \(1.4\times10^{10}\) years), and several intermediate lifetime nuclei gives a straight line plot with the correct slope within a few percent! These elements can all be understood in terms of essentially the same barrier being tunneled through at the different heights corresponding to the \(\alpha\) energy.
The treatment here is a slightly simplified version of the WKB method, to be discussed in detail later. Further refinements make little difference to the final result in this case.
Source: many of the topics covered in this lecture are elementary, and treated in any quantum textbook. For some of them I’ve followed (more or less) the excellent book by French and Taylor, An Introduction to Quantum Physics, Norton, 1978.
Contributor
- Michael Fowler (Beams Professor, Department of Physics, University of Virginia)


