8.3: Hydrogen Atom

A hydrogen atom consists of an electron, of charge \(-e\) and mass \(m_e\), and a proton, of charge \(+e\) and mass \(m_p\), moving in the Coulomb potential \[V({\bf r}) = - \frac{e^{\,2}}{4\pi\,\epsilon_0\,|{\bf r}|},\] where \({\bf r}\) is the position vector of the electron with respect to the proton. Now, according to the analysis in Section [stwo], this two-body problem can be converted into an equivalent one-body problem. In the latter problem, a particle of mass \[\mu = \frac{m_e\,m_p}{m_e+m_p}\] moves in the central potential \[V(r) = - \frac{e^{\,2}}{4\pi\,\epsilon_0\,r}.\] Note, however, that because \(m_e/m_p\simeq 1/1836\) the difference between \(m_e\) and \(\mu\) is very small. Hence, in the following, we shall write neglect this difference entirely.

Writing the wavefunction in the usual form, \[\psi(r,\theta,\phi) = R_{n,l}(r)\,Y_{l,m}(\theta,\phi),\] it follows from Section 1.2 that the radial function \(R_{n,l}(r)\) satisfies \[-\frac{\hbar^{\,2}}{2\,m_e}\left[\frac{d^{\,2}}{dr^{\,2}} + \frac{2}{r}\frac{d}{dr} -\frac{l\,(l+1)}{r^{\,2}}\right] R_{n,l} -\left(\frac{e^{\,2}}{4\pi\,\epsilon_0\,r}+E \right) R_{n,l}= 0.\] Let \(r = a\,z\), with

\[\label{e9.45} a = \sqrt{\frac{\hbar^{\,2}}{2\,m_e\,(-E)}}=\sqrt{\frac{E_0}{E}}\,a_0,\] where \(E_0\) and \(a_0\) are defined in Equations ([e9.56]) and ([e9.57]), respectively. Here, it is assumed that \(E<0\), because we are only interested in bound-states of the hydrogen atom. The previous differential equation transforms to \[\left[\frac{d^{\,2}}{dz^{\,2}} + \frac{2}{z}\frac{d}{dz}-\frac{l\,(l+1)}{z^{\,2}}+ \frac{\zeta}{z}-1\right] R_{n,l} = 0,\] where

\[\label{e9.47} \zeta = \frac{2\,m_e\,a\,e^{\,2}}{4\pi\,\epsilon_0\,\hbar^{\,2}}=2\sqrt{\frac{E_0}{E}}.\] Suppose that \(R_{n,l}(r) = Z(r/a)\,\exp(-r/a)/(r/a)\). It follows that

\[\label{e9.48} \left[\frac{d^{\,2}}{dz^{\,2}} -2\,\frac{d}{dz} - \frac{l\,(l+1)}{z^{\,2}} + \frac{\zeta}{z}\right] Z = 0.\] We now need to solve the previous differential equation in the domain \(z=0\) to \(z= \infty\), subject to the constraint that \(R_{n,l}(r)\) be square-integrable.

Let us look for a power-law solution of the form

\[\label{e9.49} Z(z) = \sum_k c_k\,z^{\,k}.\] Substituting this solution into Equation ([e9.48]), we obtain \[\sum_k c_k\left\{k\,(k-1)\,z^{\,k-2} - 2\,k\,z^{\,k-1} - l\,(l+1)\,z^{\,k-2} + \zeta\,z^{\,k-1}\right\} = 0.\] Equating the coefficients of \(z^{\,k-2}\) gives the recursion relation

\[\label{e9.51} c_k\,\left[k\,(k-1)-l\,(l+1)\right] = c_{k-1}\,\left[2\,(k-1) - \zeta\right].\] Now, the power series ([e9.49]) must terminate at small \(k\), at some positive value of \(k\), otherwise \(Z(z)\) behaves unphysically as \(z\rightarrow 0\) [i.e., it yields an \(R_{n,l}(r)\) that is not square integrable as \(r\rightarrow 0\)]. From the previous recursion relation, this is only possible if \([k_{\rm min}\,(k_{\rm min}-1)-l\,(l+1)]=0\), where the first term in the series is \(c_{k_{\rm min}}\,z^{\,k_{\rm min}}\). There are two possibilities: \(k_{\rm min}=-l\) or \(k_{\rm min}=l+1\). However, the former possibility predicts unphysical behavior of \(Z(z)\) at \(z=0\). Thus, we conclude that \(k_{\rm min}=l+1\). Note that, because \(R_{n,l}(r)\simeq Z(r/a)/(r/a)\simeq (r/a)^{\,l}\) at small \(r\), there is a finite probability of finding the electron at the nucleus for an \(l=0\) state, whereas there is zero probability of finding the electron at the nucleus for an \(l>0\) state [i.e., \(|\psi|^{\,2}=0\) at \(r=0\), except when \(l=0\)].

For large values of \(z\), the ratio of successive coefficients in the power series ([e9.49]) is \[\frac{c_k}{c_{k-1}} = \frac{2}{k},\] according to Equation ([e9.51]). This is the same as the ratio of successive coefficients in the power series \[\sum_k \frac{(2\,z)^{\,k}}{k!},\] which converges to \(\exp(2\,z)\). We conclude that \(Z(z)\rightarrow \exp(2\,z)\) as \(z\rightarrow\infty\). It thus follows that \(R_{n,l}(r)\sim Z(r/a)\,\exp(-r/a)/(r/a)\rightarrow \exp(r/a)/(r/a)\) as \(r\rightarrow\infty\). This does not correspond to physically acceptable behavior of the wavefunction, because \(\int|\psi|^2\,dV\) must be finite. The only way in which we can avoid this unphysical behavior is if the power series ([e9.49]) terminates at some maximum value of \(k\). According to the recursion relation ([e9.51]), this is only possible if

\[\label{e9.54} \frac{\zeta}{2} = n,\] where \(n\) is an integer, and the last term in the series is \(c_n\,z^{\,n}\). Because the first term in the series is \(c_{l+1}\,z^{\,l+1}\), it follows that \(n\) must be greater than \(l\), otherwise there are no terms in the series at all. Finally, it is clear from Equations ([e9.45]), ([e9.47]), and ([e9.54]) that

\[\label{e9.55} E = \frac{E_0}{n^{\,2}}\] and \[a = n\,a_0,\] where

\[\label{e9.56} E_0 = -\frac{m_e\,e^{\,4}}{2\,(4\pi\,\epsilon_0)^2\,\hbar^{\,2}} = - \frac{e^{\,2}}{8\pi\,\epsilon_0\,a_0} = -13.6\,{\rm eV},\] and

\[\label{e9.57} a_0 = \frac{4\pi\,\epsilon_0\,\hbar^{\,2}}{m_e\,e^{\,2}} = 5.3\times 10^{-11}\,{\rm m}.\] Here, \(E_0\) is the energy of so-called ground-state (or lowest energy state) of the hydrogen atom, and the length \(a_0\) is known as the Bohr radius. Note that \(|E_0|\sim \alpha^{\,2}\,m_e\,c^{\,2}\), where \(\alpha = e^{\,2}/ (4\pi\,\epsilon_0\,\hbar\,c)\simeq 1/137\) is the dimensionless fine-structure constant. The fact that \(|E_0|\ll m_e\,c^{\,2}\) is the ultimate justification for our non-relativistic treatment of the hydrogen atom.

We conclude that the wavefunction of a hydrogen atom takes the form

\[\label{e9.59} \psi_{n,l,m}(r,\theta,\phi) = R_{n,l}(r)\,Y_{l,m}(\theta,\phi).\] Here, the \(Y_{l,m}(\theta,\phi)\) are the spherical harmonics (see Section [sharm]), and \(R_{n,l}(z=r/a)\) is the solution of \[\left[\frac{1}{z^{\,2}}\,\frac{d}{dz}\,z^{\,2}\,\frac{d}{dz}- \frac{l\,(l+1)}{z^{\,2}} + \frac{2\,n}{z}-1\right] R_{n,l} = 0\] which varies as \(z^{\,l}\) at small \(z\). Furthermore, the quantum numbers \(n\), \(l\), and \(m\) can only take values that satisfy the inequality

\[\label{e9.61} |m| \leq l < n,\] where \(n\) is a positive integer, \(l\) a non-negative integer, and \(m\) an integer.

We expect the stationary states of the hydrogen atom to be orthonormal: that is, \[\int \psi^\ast_{n',l',m'}\,\psi_{n,l,m}\,dV = \delta_{nn'}\,\delta_{ll'}\,\delta_{mm'},\] where \(dV\) is a volume element, and the integral is over all space. Of course, \(dV = r^{\,2}\,dr\,d{\mit\Omega}\), where \(d{\mit\Omega}\) is an element of solid angle. Moreover, we already know that the spherical harmonics are orthonormal [see Equation ([spho])]: that is, \[\oint Y_{l',m'}^{\,\ast}\,Y_{l,m}\,d{\mit\Omega} = \delta_{ll'}\,\delta_{mm'}.\] It, thus, follows that the radial wavefunction satisfies the orthonormality constraint \[\int_0^{\infty} R_{n',l}^\ast\,R_{n,l}\,r^{\,2}\,dr = \delta_{nn'}.\] The first few radial wavefunctions for the hydrogen atom are listed below: \[\begin{aligned} R_{1,0}(r)&= \frac{2}{a_0^{\,3/2}}\,\exp\left(-\frac{r}{a_0}\right),\\[0.5ex] R_{2,0}(r) &= \frac{2}{(2\,a_0)^{3/2}}\left(1-\frac{r}{2\,a_0}\right) \exp\left(-\frac{r}{2\,a_0}\right),\\[0.5ex] R_{2,1}(r)&= \frac{1}{\sqrt{3}\,(2\,a_0)^{3/2}}\,\frac{r}{a_0}\, \exp\left(-\frac{r}{2\,a_0}\right),\\[0.5ex] R_{3,0}(r)&= \frac{2}{(3\,a_0)^{3/2}}\left(1- \frac{2\,r}{3\,a_0} + \frac{2\,r^{\,2}}{27\,a_0^{\,2}}\right)\exp\left(-\frac{r}{3\,a_0}\right),\\[0.5ex] R_{3,1}(r) &= \frac{4\sqrt{2}}{9\,(3\,a_0)^{3/2}}\,\frac{r}{a_0} \left(1-\frac{r}{6\,a_0}\right)\,\exp\left(-\frac{r}{3\,a_0}\right),\\[0.5ex] R_{3,2}(r)&= \frac{2\sqrt{2}}{27\sqrt{5}\,(3\,a_0)^{3/2}} \left(\frac{r}{a_0}\right)^2 \exp\left(-\frac{r}{3\,a_0}\right).\end{aligned}\] These functions are illustrated in Figures [coul1] and [coul2].

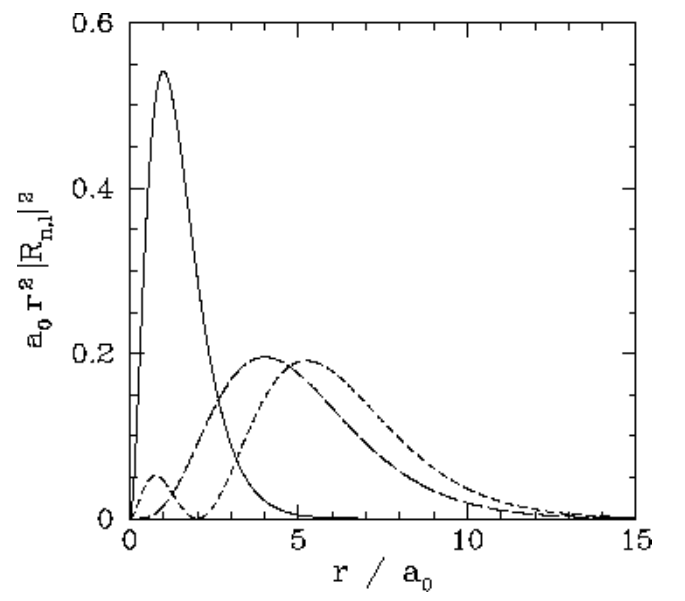
Figure 21: The \(\begin{equation}a_{0} r^{2}\left|R_{n, l}(r)\right|^{2}\end{equation}\) plotted as a functions of  \(\begin{equation}r / a_{0}\end{equation}\). The solid, short-dashed, and long-dashed curves correspond to \(\begin{equation}n, l=1,0, \text { and } 2,0, \text { and } 2,1,\end{equation}\) respectively.

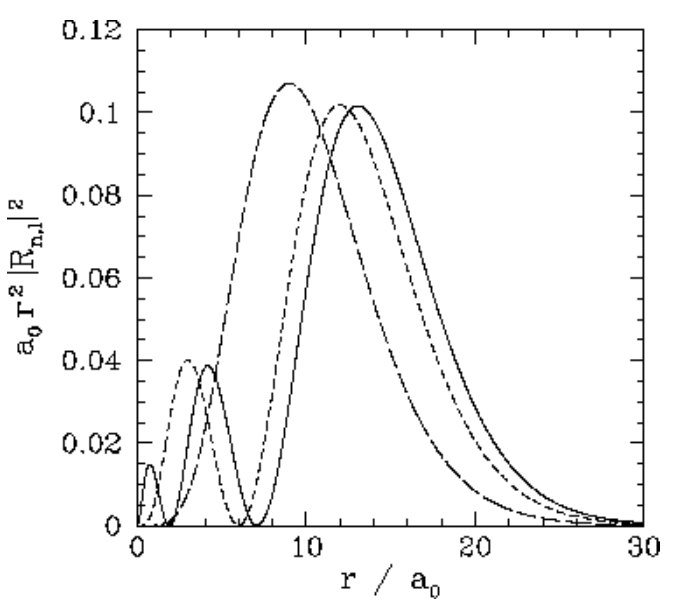
Figure 22: The \(\begin{equation}a_{0} r^{2}\left|R_{n, l}(r)\right|^{2}\end{equation}\) plotted as a functions of  \(\begin{equation}r / a_{0}\end{equation}\).The solid, short-dashed, and long-dashed curves correspond to \(\begin{equation}n, l=3,0, \text { and } 3,1, \text { and } 3,2,\end{equation}\) respectively. 

Given the (properly normalized) hydrogen wavefunction ([e9.59]), plus our interpretation of \(|\psi|^{\,2}\) as a probability density, we can calculate \[\langle r^{\,k}\rangle = \int_0^\infty r^{\,2+k}\,|R_{n,l}(r)|^{\,2}\,dr,\] where the angle-brackets denote an expectation value. For instance, it can be demonstrated (after much tedious algebra) that

\[\begin{aligned} \langle r^{\,2}\rangle &= \frac{a_0^{\,2}\,n^{\,2}}{2}\,[5\,n^{\,2}+1-3\,l\,(l+1)],\label{e9.73}\\[0.5ex] \langle r\rangle &= \frac{a_0}{2}\,[3\,n^{\,2}-l\,(l+1)],\\[0.5ex] \left\langle \frac{1}{r}\right\rangle &= \frac{1}{n^{\,2}\,a_0},\label{e9.74}\\[0.5ex] \left\langle\frac{1}{r^{\,2}}\right\rangle &= \frac{1}{(l+1/2)\,n^{\,3}\,a_0^{\,2}},\label{e9.75}\\[0.5ex] \left\langle\frac{1}{r^{\,3}}\right\rangle &=\frac{1}{l\,(l+1/2)\,(l+1)\,n^{\,3}\,a_0^{\,3}}.\label{e9.75a}\end{aligned}\]

According to Equation ([e9.55]), the energy levels of the bound-states of a hydrogen atom only depend on the radial quantum number \(n\). It turns out that this is a special property of a \(1/r\) potential. For a general central potential, \(V(r)\), the quantized energy levels of a bound-state depend on both \(n\) and \(l\). (See Section 1.3.)

The fact that the energy levels of a hydrogen atom only depend on \(n\), and not on \(l\) and \(m\), implies that the energy spectrum of a hydrogen atom is highly degenerate: that is, there are many different states which possess the same energy. According to the inequality ([e9.61]) (and the fact that \(n\), \(l\), and \(m\) are integers), for a given value of \(l\), there are \(2\,l+1\) different allowed values of \(m\) (i.e., \(-l,-l+1, \cdots, l-1, l\)). Likewise, for a given value of \(n\), there are \(n\) different allowed values of \(l\) (i.e., \(0,1,\cdots, n-1\)). Now, all states possessing the same value of \(n\) have the same energy (i.e., they are degenerate). Hence, the total number of degenerate states corresponding to a given value of \(n\) is \[1 + 3 + 5 + \cdots +2\,(n-1)+1 = n^{\,2}.\] Thus, the ground-state (\(n=1\)) is not degenerate, the first excited state (\(n=2\)) is four-fold degenerate, the second excited state (\(n=3\)) is nine-fold degenerate, et cetera (Actually, when we take into account the two spin states of an electron, the degeneracy of the \(n\)th energy level becomes \(2\,n^{\,2}\).)

Contributors and Attributions

• Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

  \( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)