13.6: Locality and Quantum Mechanics
- Page ID
- 5894
Introduction
You may be aware of the fact that Einstein never accepted Quantum Mechanics. He explained his objections by discussing two particular aspects of the theory. One was the fact that the theory is probabilistic, and seems to imply that the future is random. Einstein repeatedly said "God does not play dice with the universe," to which Bohr responded "Quit telling God what to do!" The probabilistic nature of cause and effect in Quantum Mechanics is pinpointed particularly well by the Schrödinger's Cat paradox.
The second aspect of Quantum Mechanics that greatly bothered Einstein is what he called a "spooky action at a distance" implied by the theory. Often this aspect of the theory is characterized as non-locality.
Locality means the reasonable assumption that no signal can travel faster than the speed of light. This imposes constraints on cause and effect. Thus, if we send a signal traveling at light speed to Alpha Centarui, which is 4.5 light years away from us, that signal will have no effect on Alpha Centauri for 4.5 years: locality says it is impossible to cause some effect on Alpha Centauri any faster than this. If we send a signal at light speed to the other side of a room which is about 10 meters away, the signal can have an effect in about 3 billionths of a second: the other side of the room is more local than Alpha Centauri.
As we shall see, locality is in some conflict with Quantum Mechanics.To illustrate the conflict we will only need the fact that we can view phenomena such as light as both a wave and as a particle.
The following discussion is at the level of an upper year liberal arts course in modern physics without mathematics that is given at the University of Toronto.
Mach-Zehnder Interferometer
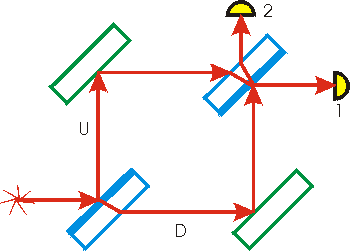 We shall use the Mach-Zehnder Interferometer to illustrate non-locality. The device, co-invented by Ernst Mach, the "grandfather" of the Theories of Relativity, is shown to the right:
We shall use the Mach-Zehnder Interferometer to illustrate non-locality. The device, co-invented by Ernst Mach, the "grandfather" of the Theories of Relativity, is shown to the right:
The legend for the figure is shown to the left.
Recall that a "half-silvered mirror" is a mirror that only reflects one-half of the light incident on it; the other half is transmitted through the mirror. In the figure, the reflecting surface is drawn as the thick one.
| Light source: | Mirror: |  | |
| Detector: |  | Half-silvered mirror: |  |
Light leaves the source and travels to the first half-silvered mirror. One half of the light is reflected as the upper U beam, which is reflected by the upper-left mirror, and travels to the upper-right half-silvered mirror. There, one half of the beam is transmitted to Detector 1, and the other half is reflected into Detector 2.
From the lower-left half-silvered mirror, the lower D beam is reflected by the lower-right mirror, and travels to the upper-right half-silvered mirror. There, one half of the beam is reflected to Detector 1, and the other half is transmitted into Detector 2
It turns out that, despite contrary appearances in the figure, all of the light that leaves the source ends up in Detector 1; no light enters Detector 2. What is happening is that the two beams, U and D, constructively interfere at Detector 1 and destructively interfere at Detector 2. The details of why this is so are sort of complex and not important for our purpose here. Those details are related to the fact that when light goes from one medium to another various "phase changes" occur.
This type of interferometer is still in regular use in laboratories around the world. It turns out that the balance of constructive and destructive interference at the detectors is extremely sensitive to any phase changes in the two beams of light. Thus, by inserting, say, a gas sample into the path of one of the beams, the additional phase shift caused by the gas allows the deduction of information on the density, pressure and temperature of the gas by observing the changes in intensity of the signals arriving at the two detectors.
Another Interferometer Arrangement
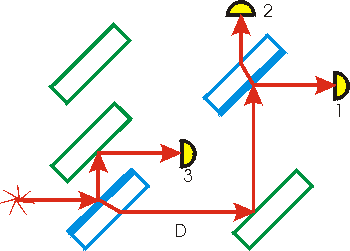 Now consider the arrangement to the right. A third mirror deflects all of the upper U beam to a third detector. Now there can not be any interference effects at detectors 1 and 2 because there is only one beam reaching the upper-right half-silvered mirror. This beam is made up of one-half of the light from the source; the other half is reflected by the lower-left half-silvered mirror and ends up in detector 3.
Now consider the arrangement to the right. A third mirror deflects all of the upper U beam to a third detector. Now there can not be any interference effects at detectors 1 and 2 because there is only one beam reaching the upper-right half-silvered mirror. This beam is made up of one-half of the light from the source; the other half is reflected by the lower-left half-silvered mirror and ends up in detector 3.
In summary, for this arrangement, the percentages of the light leaving the source that arrive at the detectors are:
| Detector | Percentage of Light from Source |
|---|---|
| 1 | 25% |
| 2 | 25% |
| 3 | 50% |
Now we begin to think of the light in the interferometer as photons, its particulate aspect. In the arrangement discussed in this section, 25% of the photons that leave the source end up in detector 2. Think for a moment about one of those photons. It travels along the lower path D and ends up in the detector. It can only end up in that detector if the third mirror is deflecting the U beam. But how did that photon "know" whether or not the U beam was being deflected? It was never anywhere near the third mirror.
It is here that we see a hint of non-locality. The existence of a third mirror that is deflecting the U beam has an immediate non-local effect on photons that were never near that mirror.
This non-locality is consistent with Quantum Mechanics, and can be demonstrated in other circumstances. For example, we consider the double slit experiment for electrons. There are positions at the observing screen where electrons will not go when both slits are open, the minima in the interference pattern. But with only one slit open, some electrons do go to that position on the screen. So if an electron goes through, say, the upper slit it seems to "know" whether or not the lower slit is open, so it knows whether or not it can go to one of the positions of the minima in the interference pattern.
Conclusion
The potential conflict between locality and Quantum Mechanics has been known since at least the early 1930's, and was the focus of a famous paper by Einstein, Pololsky and Rosen (EPR) in 1934. In that paper, they concluded that Quantum Mechanics must be at least incomplete.
The possible non-local and/or probabilistic nature of cause and effect is explored more deeply by Bell's Theorem of 1964 and its subsequent experimental tests. A document on Bell's Theorem is available here
Both for the material discussed here and especially in commentary about Bell's Theorem, one sometimes sees statements that according to Quantum Mechanics one may transmit information at speeds greater than the speed of light. I have never seen such an argument that I believe is correct. Whatever is being transmitted at superluminal speeds is somewhat less than information; d'Espagnat uses the word influence.
If we have some influence or even information being transmitted at superluminal speed from A to B, then according to the Special Theory of Relativity there are reference frames where the influence is traveling from B to A; the influence is still traveling faster than the speed of light with respect to all observers. The conclusion is that any superluminal influence has to be viewed as a connection between A and B, and identifying which is the cause and which is the effect is problematic.
A JPU200Y student recently made a startling suggestion that the influence can be traveling at superluminal speeds via a mini-blackhole wormhole connection, ie. through the quantum foam that we have seen pervades space time at very small distances.


