2.E: Geometry of Flat Spacetime (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Suppose that we don’t yet know the exact form of the Lorentz transformation, but we know based on the Michelson-Morley experiment that the speed of light is the same in all inertial frames, and we’ve already determined, e.g., by arguments like those earlier, that there can be no length contraction in the direction perpendicular to the motion. We construct a “light clock,” consisting simply of two mirrors facing each other, with a light pulse bouncing back and forth between them.
- Suppose this light clock is moving at a constant velocity v in the direction perpendicular to its own optical arm, which is of length L. Use the Pythagorean theorem to prove that the clock experiences a time dilation given by γ=1/√1−v2, thereby fixing the time-time portion of the Lorentz transformation.
- Why is it significant for the interpretation of special relativity that the result from part a is independent of L?
- Carry out a similar calculation in the case where the clock moves with constant acceleration a as measured in some inertial frame. Although the result depends on L, prove that in the limit of small L, we recover the earlier constant-velocity result, with no explicit dependence on a.
Note
Some authors state a “clock postulate” for special relativity, which says that for a clock that is sufficiently small, the rate at which it runs depends only on v, not a (except in the trivial sense that v and a are related by calculus). The result of part c shows that the clock “postulate” is really a theorem, not a statement that is logically independent of the other postulates of special relativity. Although this argument only applies to a particular family of light clocks of various sizes, one can also make any small clock into an acceleration-insensitive clock, by attaching an accelerometer to it and applying an appropriate correction to compensate for the clock’s observed sensitivity to acceleration. (It’s still necessary for the clock to be small, since otherwise the lack of simultaneity in relativity makes it impossible to describe the whole clock as having a certain acceleration at a certain instant.) Farley at al.22 have verified the “clock postulate” to within 2% for the radioactive decay of muons with γ ∼ 12 being accelerated by magnetic fields at 5 × 1018 m/s2. Some people get confused by this acceleration-independent property of small clocks and think that it contradicts the equivalence principle. For a good explanation, see http://math.ucr.edu/home/baez/physics/Relativity/SR/clock.html.
22 Nuovo Cimento 45 (1966) 281
- Some of the most conceptually direct tests of relativistic time dilation were carried out by comparing the rates of twin atomic clocks, one left on a mountaintop for a certain amount of time, the other in a nearby valley below.23 Unlike the clocks in the Hafele-Keating experiment, these are stationary for almost the entire duration of the experiment, so any time dilation is purely gravitational, not kinematic. One could object, however, that the clocks are not really at rest relative to one another, due to the earth’s rotation. This is an example of how the distinction between gravitational and kinematic time dilations is frame-dependent, since the effect is purely gravitational in the rotating frame, where the gravitational field is reduced by the fictitious centrifugal force. Show that, in the non-rotating frame, the ratio of the kinematic effect to the gravitational one comes out to be 2.8 × 10−3 at the latitude of Tokyo. This small value indicates that the experiment can be interpreted as a very pure test of the gravitational time dilation effect. To calculate the effect, you will need to use the fact that, as discussed earlier, gravitational redshifts can be interpreted as gravitational time dilations.
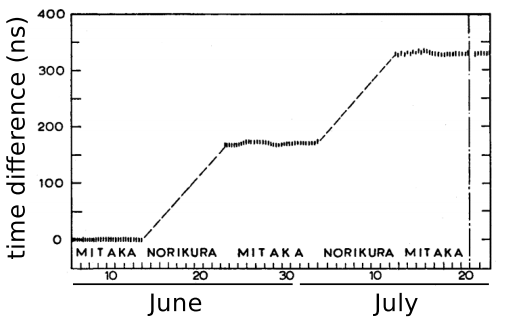
A graph from the paper by Iijima, showing the time difference between the two clocks. One clock was kept at Mitaka Observatory, at 58 m above sea level. The other was moved back and forth between a second observatory, Norikura Corona Station, and the peak of the Norikura volcano, 2876 m above sea level. The plateaus on the graph are data from the periods when the clocks were compared side by side at Mitaka. The difference between one plateau and the next is the gravitational time dilation accumulated during the period when the mobile clock was at the top of Norikura.
Note
L. Briatore and S. Leschiutta, “Evidence for the earth gravitational shift by direct atomic-time-scale comparison,” Il Nuovo Cimento B, 37B (2): 219 (1977). Iijima et al., “An experiment for the potential blue shift at the Norikura Corona Station,” Annals of the Tokyo Astronomical Observatory, Second Series, Vol. XVII, 2 (1978) 68.
- (a) In Figure 2.5.10, we showed that the Thomas precession is proportional to area on the velocity disk. Use a similar argument to show that the Sagnac effect is proportional to the area enclosed by the loop. (b) Verify this more directly in the special case of a circular loop. (c) Show that a light clock of the type described in problem 1 is insensitive to rotation with constant angular velocity. (d) Connect these results to the commutativity and transitivity assumptions in the Einstein clock synchronization procedure described later.
- Example 14 discusses relativistic bounds on the properties of matter, using the example of pulling a bucket out of a black hole. Derive a similar bound by considering the possibility of sending signals out of the black hole using longitudinal vibrations of a cable, as in the child’s telephone made of two tin cans connected by a piece of string.
Note
Surprisingly subtle issues can arise in such calculations; see A.Y. Shiekh, Can. J. Phys. 70, 458 (1992). For a quantitative treatment of a dangling rope in relativity, see Greg Egan, “The Rindler Horizon,” http://gregegan.customer.netspace.net.au/SCIENCE/Rindler/RindlerHorizon.html.
- The Maxima program demonstrates how to multiply matrices and find Taylor series. Apply this technique to the following problem. For successive Lorentz boosts along the same axis with rapidities η1 and η2, find the matrix representing the combined Lorentz transformation, in a Taylor series up to the first nonclassical terms in each matrix element. A mixed Taylor series in two variables can be obtained simply by nesting taylor functions. The taylor function will happily work on matrices, not just scalars.


