3.3: Affine Notions and Parallel Transport
( \newcommand{\kernel}{\mathrm{null}\,}\)
The Affine Parameter in Curved Spacetime: A Rough Sketch
We want to be able to measure things in curved spacetime. There turn out to be two complementary systems of measurement we can apply: affine measure and metric measure. Affine measure in a flat geometry was introduced in Section 2.1. Surprisingly, it turns out to be quite easy to generalize this to the curved case. Our construction of the affine parameter with a scaffolding of parallelograms depended on the existence and uniqueness of parallels expressed by axiom A1, so we might imagine that there was no point in trying to generalize the construction to curved spacetime. But the equivalence principle tells us that spacetime is locally affine to some approximation. Concretely, clock-time is one example of an affine parameter, and the curvature of spacetime clearly can’t prevent us from building a clock and releasing it on a free-fall trajectory.
More generally, we can use the fact that every segment of a geodesic is geometrically similar to every other segment. For example, consider an arc of the earth’s equator spanning one degree of longitude. That arc could be slid along the equator to a different location, then expanded to cover 3 degrees of longitude. The two arcs are similar.
Example 2: Geodesics are special
The following three non-examples show that this is a special property of geodesics.
The property is not enjoyed by a non-geodesic curve. A segment of a pentagon that encompasses one of the vertices is not similar to some other segment that is straight.
Another non-example involving non-geodesics is the curve that we get in 1+1-dimensional spacetime by joining together the positive x axis and the positive t axis. We can never take a one-year segment of the t axis and, through any combination of boosts and rotations, make it coincide with a one-light-year piece of the x axis. The original segment is timelike, and any boost or rotation will preserve its timelike character.
Furthermore, it is not true in general, when curvature exists, that we can take any geometrical figure, transport it wherever we like, and also scale it as we like. For example, Euclidean geometry is a good approximation on small portions of the Earth’s spherical surface, so a roadmap can be made in the shape of a rectangle with four right-angle corners. However, it is not possible to scale up such a rectangle; to map a large portion of the world, we have to introduce distortions of the type used in map projections.
Because geodesics have this special property, we can slide any portion of a geodesic to anywhere else on the geodesic and employ it as a standard of measure. This gives us a complete system of measurement along that geodesic, and it works regardless of whether the geodesic is timelike, lightlike, or spacelike. But as in flat geometry, affine measurement does not allow us to compare lengths along one geodesic to lengths along another.
The Affine Parameter in More Detail
When we originally defined affine measure in Section 2.1, for a flat space, we did it through the explicit construction of a scaffolding. An important example of the differential, i.e., local, nature of our geometry is the generalization of the scaffolding construction from to a context broader than affine geometry.
To generalize the recipe for the construction (Figure 3.2.1), the first obstacle is the ambiguity of the instruction to construct parallelogram (0,1,q0,q1), which requires us to draw 1q1 parallel to 0q0. Suppose we construe this as an instruction to make the two segments initially parallel, i.e., parallel as they depart the line at 0 and 1. By the time they get to q0 and q1, they may be converging or diverging.
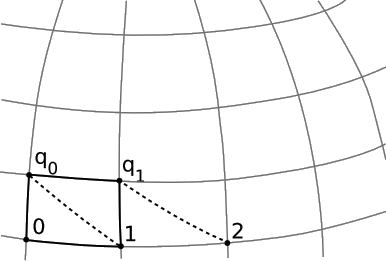
Because parallelism is only approximate here, there will be a certain amount of error in the construction of the affine parameter. One way of detecting such an error is that lattices constructed with different initial distances will get out of step with one another. For example, we can define 12 as before by requiring that the lattice constructed with initial segment 0 12 line up with the original lattice at 1. We will find, however, that they do not quite line up at other points, such as 2. Let’s use this discrepancy ϵ = 2 − 2' as a numerical measure of the error. It will depend on both δ1, the distance 01, and on δ2, the distance between 0 and q0. Since ϵ vanishes for either δ1 = 0 or δ2 = 0, and since the equivalence principle guarantees smooth behavior on small scales, the leading term in the error will in general be proportional to the product δ1δ2. In the language of infinitesimals, we can replace δ1 and δ2 with infinitesimally short distances, which for simplicity we assume to be equal, and which we call dλ. Then the affine parameter λ is defined as λ=∫dλ, where the error of order dλ2 is, as usual, interpreted as the negligible discrepancy between the integral and its approximation as a Riemann sum.
Parallel Transport
If you were alert, you may have realized that I cheated you at a crucial point in this construction. We were to make 1q1 and 0q0 “initially parallel” as they left 01. How should we even define this idea of “initially parallel?” We could try to do it by making angles q001 and q112 equal, but this doesn’t quite work, because it doesn’t specify whether the angle is to the left or the right on the two-dimensional plane of the page. In three or more dimensions, the issue becomes even more serious. The construction workers building the lattice need to keep it all in one plane, but how do they do that in curved spacetime?
A mathematician’s answer would be that our geometry lacks some additional structure called a connection, which is a rule that specifies how one locally flat neighborhood is to be joined seamlessly onto another locally flat neighborhood nearby. If you’ve ever bought two maps and tried to tape them together to make a big map, you’ve formed a connection. If the maps were on a large enough scale, you also probably noticed that this was impossible to do perfectly, because of the curvature of the earth.
Physically, the idea is that in flat spacetime, it is possible to construct inertial guidance systems like the ones discussed earlier. Since they are possible in flat spacetime, they are also possible in locally flat neighborhoods of spacetime, and they can then be carried from one neighborhood to another. In three space dimensions, a gyroscope’s angular momentum vector maintains its direction, and we can orient other vectors, such as 1q1, relative to it. Suppose for concreteness that the construction of the affine parameter above is being carried out in three space dimensions. We place a gyroscope at 0, orient its axis along 0q0 , slide it along the line to 1, and then construct 1q1 along that axis.
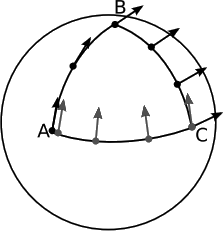
In 3+1 dimensions, a gyroscope only does part of the job. We now have to maintain the direction of a four-dimensional vector. Four-vectors will not be discussed in detail until section 4.2, but similar devices can be used to maintain their orientations in spacetime. These physical devices are ways of defining a mathematical notion known as parallel transport, which allows us to take a vector from one point to another in space. In general, specifying a notion of parallel transport is equivalent to specifying a connection.
Parallel transport is path-dependent, as shown in Figure 3.2.2.
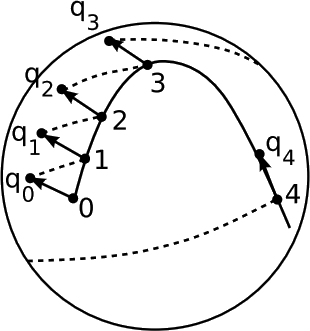
Affine Parameters Defined Only along Geodesics
In the context of flat spacetime, the affine parameter was defined only along lines, not arbitrary curves, and could not be compared between lines running in different directions. In curved spacetime, the same limitation is present, but with “along lines” replaced by “along geodesics.” Figure 3.2.3 shows what goes wrong if we try to apply the construction to a world-line that isn’t a geodesic. One definition of a geodesic is that it’s the course we’ll end up following if we navigate by keeping a fixed bearing relative to an inertial guidance device such as gyroscope; that is, the tangent to a geodesic, when parallel-transported farther along the geodesic, is still tangent. A non-geodesic curve lacks this property, and the effect on the construction of the affine parameter is that the segments nqn drift more and more out of alignment with the curve.