3.4: Models
- Page ID
- 10427
A typical first reaction to the phrase “curved spacetime” — or even “curved space,” for that matter — is that it sounds like nonsense. How can featureless, empty space itself be curved or distorted? The concept of a distortion would seem to imply taking all the points and shoving them around in various directions as in a Picasso painting, so that distances between points are altered. But if space has no identifiable dents or scratches, it would seem impossible to determine which old points had been sent to which new points, and the distortion would have no observable effect at all. Why should we expect to be able to build differential geometry on such a logically dubious foundation? Indeed, historically, various mathematicians have had strong doubts about the logical self-consistency of both non-Euclidean geometry and infinitesimals. And even if an authoritative source assures you that the resulting system is self-consistent, its mysterious and abstract nature would seem to make it difficult for you to develop any working picture of the theory that could play the role that mental sketches of graphs play in organizing your knowledge of calculus.

Models provide a way of dealing with both the logical issues and the conceptual ones. Figure 3.2.1 “pops” off of the page, presenting a strong psychological impression of a curved surface rendered in perspective. This suggests finding an actual mathematical object, such as a curved surface, that satisfies all the axioms of a certain logical system, such as non-Euclidean geometry. Note that the model may contain extrinsic elements, such as the existence of a third dimension, that are not connected to the system being modeled.
Let’s focus first on consistency. In general, what can we say about the self-consistency of a mathematical system? To start with, we can never prove anything about the consistency or lack of consistency of something that is not a well-defined formal system, e.g., the Bible. Even Euclid’s Elements, which was a model of formal rigor for thousands of years, is loose enough to allow considerable ambiguity. If you’re inclined to scoff at the silly Renaissance mathematicians who kept trying to prove the parallel postulate E5 from postulates E1-E4, consider the following argument. Suppose that we replace E5 with E5', which states that parallels don’t exist: given a line and a point not on the line, no line can ever be drawn through the point and parallel to the given line. In the new system of plane geometry E' consisting of E1-E4 plus E5', we can prove a variety of theorems, and one of them is that there is an upper limit on the area of any figure. This imposes a limit on the size of circles, and that appears to contradict E3, which says we can construct a circle with any radius.
We therefore conclude that E' lacks self-consistency. Oops! As your high school geometry text undoubtedly mentioned in passing, E' is a perfectly respectable system called elliptic geometry. So what’s wrong with this supposed proof of its lack of self-consistency? The issue is the exact statement of E3. E3 does not say that we can construct a circle given any real number as its radius. Euclid could not have intended any such interpretation, since he had no notion of real numbers. To Euclid, geometry was primary, and numbers were geometrically constructed objects, being represented as lengths, angles, areas, and volumes. A literal translation of Euclid’s statement of the axiom is “To describe a circle with any center and distance.”1 “Distance” means a line segment. There is therefore no contradiction in E', because E' has a limit on the lengths of line segments.
Now suppose that such ambiguities have been eliminated from the system’s basic definitions and axioms. In general, we expect it to be easier to prove an inconsistent system’s inconsistency than to demonstrate the consistency of a consistent one. In the former case, we can start cranking out theorems, and if we can find a way to prove both proposition P and its negation ¬P, then obviously something is wrong with the system. One might wonder whether such a contradiction could remain contained within one corner of the system, like nuclear waste. It can’t. Aristotelian logic allows proof by contradiction: if we prove both P and ¬P based on certain assumptions, then our assumptions must have been wrong. If we can prove both P and ¬P without making any assumptions, then proof by contradiction allows us to establish the truth of any randomly chosen proposition. Thus a single contradiction is sufficient, in Aristotelian logic, to invalidate the entire system. This goes by the Latin rubric ex falso quodlibet, meaning “from a falsehood, whatever you please.” Thus any contradiction proves the inconsistency of the entire system.
Proving consistency is harder. If you’re mathematically sophisticated, you may be tempted to leap directly to Gödel’s theorem, and state that nobody can ever prove the self-consistency of a mathematical system. This would be a misapplication of Gödel. Gödel’s theorem only applies to mathematical systems that meet certain technical criteria, and some of the interesting systems we’re dealing with don’t meet those criteria; in particular, Gödel’s theorem doesn’t apply to Euclidean geometry, and Euclidean geometry was proved self-consistent by Tarski and his students around 1950. Furthermore, we usually don’t require an absolute proof of self-consistency. Usually we’re satisfied if we can prove that a certain system, such as elliptic geometry, is at least as self-consistent as another system, such as Euclidean geometry. This is called equiconsistency. The general technique for proving equiconsistency of two theories is to show that a model of one can be constructed within the other.
Suppose, for example, that we construct a geometry in which the space of points is the surface of a sphere, and lines are understood to be the geodesics, i.e., the great circles whose centers coincide at the sphere’s center. This geometry, called spherical geometry, is useful in cartography and navigation. It is non-Euclidean, as we can demonstrate by exhibiting at least one proposition that is false in Euclidean geometry. For example, construct a triangle on the earth’s surface with one corner at the north pole, and the other two at the equator, separated by 90 degrees of longitude. The sum of its interior angles is 270 degrees, contradicting Euclid, book I, proposition 32. Spherical geometry must therefore violate at least one of the axioms E1-E5, and indeed it violates both E1 (because no unique line is determined by two antipodal points such as the north and south poles) and E5 (because parallels don’t exist at all).
A closely related construction gives a model of elliptic geometry, in which E1 holds, and only E5 is thrown overboard. To accomplish this, we model a point using a diameter of the sphere,2 and a line as the set of all diameters lying in a certain plane. This has the effect of identifying antipodal points, so that there is now no violation of E1. Roughly speaking, this is like lopping off half of the sphere, but making the edges wrap around. Since this model of elliptic geometry is embedded within a Euclidean space, all the axioms of elliptic geometry can now be proved as theorems in Euclidean geometry. If a contradiction arose from them, it would imply a contradiction in the axioms of Euclidean geometry. We conclude that elliptic geometry is equiconsistent with Euclidean geometry. This was known long before Tarski’s 1950 proof of Euclidean geometry’s self-consistency, but since nobody was losing any sleep over hidden contradictions in Euclidean geometry, mathematicians stopped wasting their time looking for contradictions in elliptic geometry.
Note
The term “elliptic” may be somewhat misleading here. The model is still constructed from a sphere, not an ellipsoid.
Example 3: Infinitesimals
Consider the following axiomatically defined system of numbers:
- It is a field, i.e., it has addition, subtraction, multiplication, and division with the usual properties.
- It is an ordered geometry in the sense of O1-O4, and the ordering relates to addition and multiplication in the usual way.
- Existence of infinitesimals: There exists a positive number d such that d < 1, d < 1/2, d < 1/3, . . .
A model of this system can be constructed within the real number system by defining d as the identity function d(x) = x and forming the set of functions of the form f(d) = P(d)/Q(d), where P and Q are polynomials with real coefficients. The ordering of functions f and g is defined according to the sign of \(\lim_{x \rightarrow 0^{+}}\) f(x) − g(x). Axioms 1-3 can all be proved from the real-number axioms. Therefore this system, which includes infinitesimals, is equiconsistent with the reals. More elaborate constructions can extend this to systems that have more of the properties of the reals, and a browser-based calculator that implements such a system is available at lightandmatter.com/calc/inf. Abraham Robinson extended this in 1966 to all of analysis, and thus there is nothing intrinsically nonrigorous about doing analysis in the style of Gauss and Euler, with symbols like dx representing infinitesimally small quantities.3
3 More on this topic is available in, for example, Keisler’s Elementary Calculus: An Infinitesimal Approach, Stroyan’s A Brief Introduction to Infinitesimal Calculus, or my own Calculus, all of which are available for free online.
Besides proving consistency, these models give us insight into what’s going on. The model of elliptic geometry suggests an insight into the reason that there is an upper limit on lengths and areas: it is because the space wraps around on itself. The model of infinitesimals suggests a fact that is not immediately obvious from the axioms: the infinitesimal quantities compose a hierarchy, so that for example 7d is in finite proportion to d, while d2 is like a “lesser flea” in Swift’s doggerel: “Big fleas have little fleas/ On their backs to ride ’em,/ and little fleas have lesser fleas,/And so, ad infinitum.”
Spherical and elliptic geometry are not valid models of a general-relativistic spacetime, since they are locally Euclidean rather than Lorentzian, but they still provide us with enough conceptual guidance to come up with some ideas that might never have occurred to us otherwise:
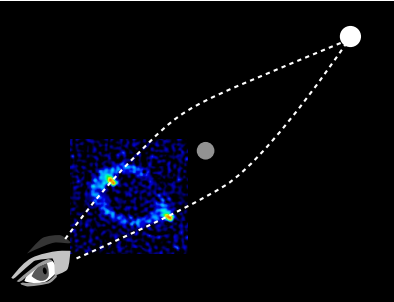
- In spherical geometry, we can have a two-sided polygon called a lune that encloses a nonzero area. In general relativity, a lune formed by the world-lines of two particles represents motion in which the particles separate but are later reunited, presumably because of some mass between them that created a gravitational field. An example is gravitational lensing.
- Both spherical models wraps around on themselves, so that they are not topologically equivalent to infinite planes. We therefore form a conjecture there may be a link between curvature, which is a local property, and topology, which is global. Such a connection is indeed observed in relativity. For example, cosmological solutions of the equations of general relativity come in two flavors. One type has enough matter in it to produce more than a certain critical amount of curvature, and this type is topologically closed. It describes a universe that has finite spatial volume, and that will only exist for a finite time before it recontracts in a Big Crunch. The other type, corresponding to the universe we actually inhabit, has infinite spatial volume, will exist for infinite time, and is topologically open.
- There is a distance scale set by the size of the sphere, with its inverse being a measure of curvature. In general relativity, we expect there to be a similar way to measure curvature numerically, although the curvature may vary from point to point.
Exercise \(\PageIndex{1}\)
Prove from the axioms E' that elliptic geometry, unlike spherical geometry, cannot have a lune with two distinct vertices. Convince yourself nevertheless, using the spherical model of E', that it is possible in elliptic geometry for two lines to enclose a region of space, in the sense that from any point P in the region, a ray emitted in any direction must intersect one of the two lines. Summarize these observations with a characterization of lunes in elliptic geometry versus lunes in spherical geometry.
References
1 Heath, pp. 195-202


