5.1: Introduction to Curvature
- Page ID
- 11458
General relativity describes gravitation as a curvature of spacetime, with matter acting as the source of the curvature in the same way that electric charge acts as the source of electric fields. Our goal is to arrive at Einstein’s field equations, which relate the local intrinsic curvature to the locally ambient matter in the same way that Gauss’s law relates the local divergence of the electric field to the charge density. The locality of the equations is necessary because relativity has no action at a distance; cause and effect propagate at a maximum velocity of \(c(= 1)\).
The hard part is arriving at the right way of defining curvature. We’ve already seen that it can be tricky to distinguish intrinsic curvature, which is real, from extrinsic curvature, which can never produce observable effects. E.g., Example 5 showed that spheres have intrinsic curvature, while cylinders do not. The manifestly intrinsic tensor notation protects us from being misled in this respect. If we can formulate a definition of curvature expressed using only tensors that are expressed without reference to any preordained coordinate system, then we know it is physically observable, and not just a superficial feature of a particular model.
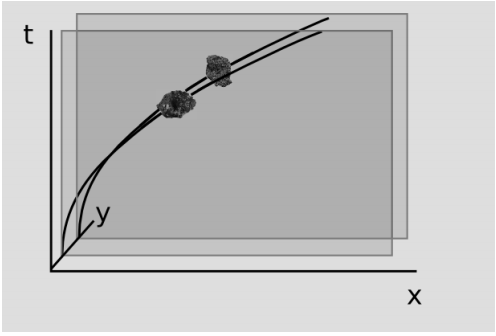
As an example, drop two rocks side by side, Figure 5.0.2. Their trajectories are vertical, but on a \((t, x)\) coordinate plot rendered in the Earth’s frame of reference, they appear as parallel parabolas. The curvature of these parabolas is extrinsic. The Earth-fixed frame of reference is defined by an observer who is subject to non-gravitational forces, and is therefore not a valid Lorentz frame. In a free-falling Lorentz frame \((t', x')\), the two rocks are either motionless or moving at constant velocity in straight lines. We can therefore see that the curvature of world-lines in a particular coordinate system is not an intrinsic measure of curvature; it can arise simply from the choice of the coordinate system. What would indicate intrinsic curvature would be, for example, if geodesics that were initially parallel were to converge or diverge.
Nor is the metric a measure of intrinsic curvature. In example 19, we found the metric for an accelerated observer to be
\[g'_{t' t'} = (1 + ax')^{2} \qquad g_{x' x'} = -1,\]
where the primes indicate the accelerated observer’s frame. The fact that the timelike element is not equal to −1 is not an indication of intrinsic curvature. It arises only from the choice of the coordinates (t', x') defined by a frame tied to the accelerating rocket ship.
The fact that the above metric has nonvanishing derivatives, unlike a constant Lorentz metric, does indicate the presence of a gravitational field. However, a gravitational field is not the same thing as intrinsic curvature. The gravitational field seen by an observer aboard the ship is, by the equivalence principle, indistinguishable from an acceleration, and indeed the Lorentzian observer in the earth’s frame does describe it as arising from the ship’s acceleration, not from a gravitational field permeating all of space. Both observers must agree that “I got plenty of nothin’ ” — that the region of the universe to which they have access lacks any stars, neutrinos, or clouds of dust. The observer aboard the ship must describe the gravitational field he detects as arising from some source very far away, perhaps a hypothetical vast sheet of lead lying billions of light-years aft of the ship’s deckplates. Such a hypothesis is fine, but it is unrelated to the structure of our hoped-for field equation, which is to be local in nature.
Not only does the metric tensor not represent the gravitational field, but no tensor can represent it. By the equivalence principle, any gravitational field seen by observer A can be eliminated by switching to the frame of a free-falling observer B who is instantaneously at rest with respect to A at a certain time. The structure of the tensor transformation law guarantees that A and B will agree on whether a given tensor is zero at the point in spacetime where they pass by one another. Since they agree on all tensors, and disagree on the gravitational field, the gravitational field cannot be a tensor.
We therefore conclude that a nonzero intrinsic curvature of the type that is to be included in the Einstein field equations is not encoded in any simple way in the metric or its first derivatives. Since neither the metric nor its first derivatives indicate curvature, we can reasonably conjecture that the curvature might be encoded in its second derivatives.


