5.2: Tidal Curvature Versus Curvature Caused by Local Sources

A further complication is the need to distinguish tidal curvature from curvature caused by local sources. Figure \(\PageIndex{1}\) shows Comet Shoemaker-Levy, broken up into a string of fragments by Jupiter’s tidal forces shortly before its spectacular impact with the planet in 1994. Immediately after each fracture, the newly separated chunks had almost zero velocity relative to one another, so once the comet finished breaking up, the fragments’ world-lines were a sheaf of nearly parallel lines separated by spatial distances of only 1 km. These initially parallel geodesics then diverged, eventually fanning out to span millions of kilometers.

Figure \(\PageIndex{1}\): Tidal forces disrupt comet Shoemaker-Levy.

If initially parallel lines lose their parallelism, that is clearly an indication of intrinsic curvature. We call it a measure of sectional curvature, because the loss of parallelism occurs within a particular plane, in this case the \((t, x)\) plane represented by Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): Tidal forces cause the initially parallel world-lines of the fragments to diverge. The spacetime occupied by the comet has intrinsic curvature, but it is not caused by any local mass; it is caused by the distant mass of Jupiter.

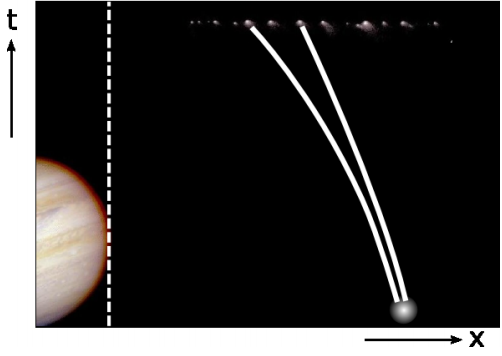
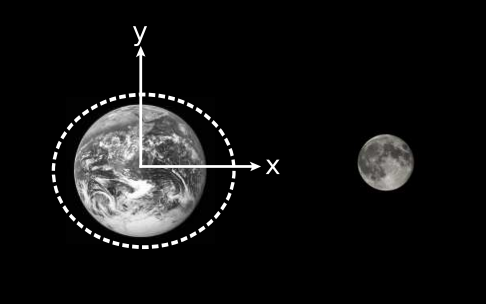
But this curvature was not caused by a local source lurking in among the fragments. It was caused by a distant source: Jupiter. We therefore see that the mere presence of sectional curvature is not enough to demonstrate the existence of local sources. Even the sign of the sectional curvature is not a reliable indication. Although this example showed a divergence of initially parallel geodesics, referred to as a negative curvature, it is also possible for tidal forces exerted by distant masses to create positive curvature. For example, the ocean tides on earth oscillate both above and below mean sea level, Figure Figure \(\PageIndex{3}\).

Figure \(\PageIndex{3}\): The moon’s gravitational field causes the Earth’s oceans to be distorted into an ellipsoid. The sign of the sectional curvature is negative in the x − t plane, but positive in the y − t plane.

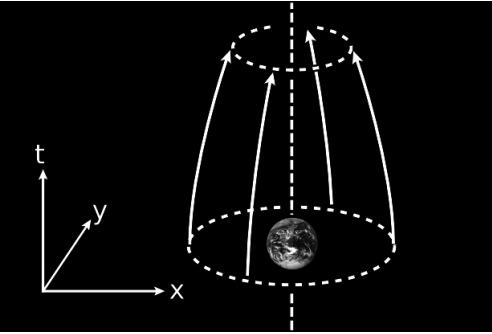
As an example that really would indicate the presence of a local source, we could release a cloud of test masses at rest in a spherical shell around the earth, and allow them to drop, Figure \(\PageIndex{4}\). We would then have positive and equal sectional curvature in the \(t − x\), \(t − y\), and \(t − z\) planes. Such an observation cannot be due to a distant mass. It demonstrates an over-all contraction of the volume of an initially parallel sheaf of geodesics, which can never be induced by tidal forces. The earth’s oceans, for example, do not change their total volume due to the tides, and this would be true even if the oceans were a gas rather than an incompressible fluid. It is a unique property of \(\frac{1}{r^{2}}\) forces such as gravity that they conserve volume in this way; this is essentially a restatement of Gauss’s law in a vacuum.

Figure \(\PageIndex{4}\): A cloud of test masses is released at rest in a spherical shell around the earth, shown here as a circle because the z axis is omitted. The volume of the shell contracts over time, which demonstrates that the local curvature of spacetime is generated by a local source — the earth — rather than some distant one.