1.E: Spacetime (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Q1
Astronauts in three different spaceships are communicating with each other. Those aboard ships A and B agree on the rate at which time is passing, but they disagree with the ones on ship C.
- Alice is aboard ship A. How does she describe the motion of her own ship, in its frame of reference?
- Describe the motion of the other two ships according to Alice.
- Give the description according to Betty, whose frame of reference is ship B.
- Do the same for Cathy, aboard ship C.
Q2
What happens in the equation for γ when you put in a negative number for v? Explain what this means physically, and why it makes sense.
Q3
The Voyager 1 space probe, launched in 1977, is moving faster relative to the earth than any other human-made object, at 17,000 meters per second.
- Calculate the probe’s γ.
- Over the course of one year on earth, slightly less than one year passes on the probe. How much less? (There are 31 million seconds in a year.)
Q4
The earth is orbiting the sun, and therefore is contracted relativistically in the direction of its motion. Compute the amount by which its diameter shrinks in this direction.
Q5
The figure shows seven displacement vectors in spacetime. Which of these represent spacetime intervals that are equal to one another?
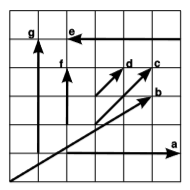
Q6
- In Euclidean geometry in three dimensions, suppose we have two vectors, a and b, which are unit vectors, i.e., a⋅a=1 and b⋅b=1. What is the range of possible values for the inner product a⋅b?
- Repeat part a for two timelike, future-directed unit vectors in 3+1 dimensions.
Q7
Expressed in natural units, the Lorentz transformation is
t′=γt−vγx′x′=−vγt+γx
- Insert factors of c to make it valid in units where \(c \neq 1\).
- Show that in the limit c→∞, these have the right Galilean behavior.
Q8
This problem assumes you have some basic knowledge of quantum physics. One way of expressing the correspondence principle as applied to special relativity is that in the limit c→∞, all relativistic expressions have to go over to their Galilean counterparts. What would be the corresponding limit if we wanted to recover classical mechanics from quantum mechanics?
Q9
In 3+1 dimensions, prove that if →u and →v are nonzero, future-lightlike, and not parallel to each other, then their sum is future-timelike.
Q10
Prove that if →u and →v are nonzero, lightlike, and orthogonal to each other, then they are parallel, i.e., →u=c→v for some c≠0.
Q11
The speed at which a disturbance travels along a string under tension is given by v=√Tμ, where μ is the mass per unit length, and T is the tension.
- Suppose a string has a density ρ, and a cross-sectional area A. Find an expression for the maximum tension that could possibly exist in the string without producing v>c, which is impossible according to relativity. Express your answer in terms of ρ, A, and c. The interpretation is that relativity puts a limit on how strong any material can be.
- Every substance has a tensile strength, defined as the force per unit area required to break it by pulling it apart. The tensile strength is measured in units of N/m2, which is the same as the pascal (Pa), the mks unit of pressure. Make a numerical estimate of the maximum tensile strength allowed by relativity in the case where the rope is made out of ordinary matter, with a density on the same order of magnitude as that of water. (For comparison, kevlar has a tensile strength of about 4×109Pa, and there is speculation that fibers made from carbon nanotubes could have values as high as 6×1010Pa.)
- A black hole is a star that has collapsed and become very dense, so that its gravity is too strong for anything ever to escape from it. For instance, the escape velocity from a black hole is greater than c, so a projectile can’t be shot out of it. Many people, when they hear this description of a black hole in terms of an escape velocity greater than c, wonder why it still wouldn’t be possible to extract an object from a black hole by other means than launching it out as a projectile. For example, suppose we lower an astronaut into a black hole on a rope, and then pull him back out again. Why might this not work?
Q12
The rod in the figure is perfectly rigid. At event A, the hammer strikes one end of the rod. At event B, the other end moves. Since the rod is perfectly rigid, it can’t compress, so A and B are simultaneous. In frame 2, B happens before A. Did the motion at the right end cause the person on the left to decide to pick up the hammer and use it?
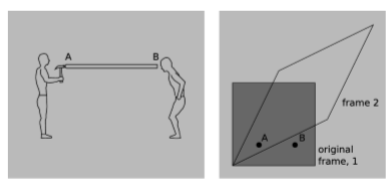
Q13
Use a spacetime diagram to resolve the following relativity paradox. Relativity says that in one frame of reference, event A could happen before event B, but in someone else’s frame B would come before A. How can this be? Obviously the two people could meet up at A and talk as they cruised past each other. Wouldn’t they have to agree on whether B had already happened?
Q14
The grid represents spacetime in a certain frame of reference. Event A is marked with a dot. Mark additional points satisfying the following criteria. (Pick points that lie at the intersections of the gridlines.)
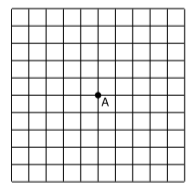
Point B is at the same location as A in this frame of reference, and lies in its future.
C is also in point A’s future, is not at the same location as A in this frame, but is in the same location as A according to some other frame of reference.
D is simultaneous with A in this frame of reference.
E is not simultaneous with A in this frame of reference, but is simultaneous with it according to some other frame.
F lies in A’s past according to this frame of reference, but could not have caused A.
G lies in A’s future according to this frame of reference, but is in its past according to some other frames.
H lies in A’s future according to any frame of reference, not just this one.
I is the departure of a spaceship, which arrives at A.
J could have caused A, but could not have been the departure of a spaceship like I that arrived later at A.
Q15
- Given an observer whose world-line is along a four-vector →O, suppose we want to determine whether some other four-vector →P is also a possible world-line of an observer. Show that knowledge of the signs of the inner products →O⋅→P and →P⋅→P is necessary and sufficient to determine this.
- Suppose that →U and →V are both observer-vectors. What would it mean physically to compute →U+overrightarrowV?
- For vectors as described in part b, determine the signs of (→U+→V)⋅(→U+→V)and (→U+→V)⋅→Uby multiplying them out. Interpret the result physically.
Q16
In section 1.5, we proved the reversed Cauchy-Schwarz inequality for two timelike vectors, without any assumption as to whether they lay in the future or past light cones. But suppose that we had only established this fact for two vectors that were both future-directed. Show that the same inequality would then also have to hold regardless of whether one or both vectors was past-directed.
Q17
In the case of two future-directed timelike vectors, complete the proof of the reversed triangle inequality using the method suggested in section 1.5.
Q18
In section 1.5 we claimed that the reversed Cauchy-Schwarz inequality holds for two spacelike vectors that span the light cone. The purpose of this problem is to prove this fact using the following sketch of an argument provided by PhysicsForums user martinbn. Suppose that spacelike vectors →m and →n span the light cone, so that we can find some real number α such that p=αm+n is lightlike. Compute p2, and show that since α is real, the reversed Cauchy- Schwarz inequality holds.
Q19
A length-contracted object has length L=L0γ Joe differentiates this with respect to time and finds dLdt=−L0vγdvdt. He reasons that there is no upper limit on the magnitude of dvdt, and therefore if v≠0 the quantity dLdt can be arbitrarily large. This means that if an object accelerates away from an observer, its trailing edge can have v>c, which is supposed to be forbidden by relativity. OMG! Is Joe’s reasoning correct?


