2.5: Lemma - Spacetime area is invariant
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- To prove from axioms P1-P6 that area in the x−t plane is invariant
In this section we prove from axioms P1-P6 that area in the x−t plane is invariant, i.e., it does not change between frames of reference. This result was used in Section 1.3 to find the form of the spacetime metric. Consider figure 2.5.1.
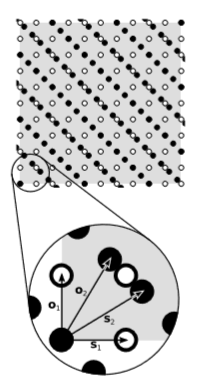
Vectors →o1 and →s1 are orthogonal and have equal lengths as measured by a clock and a ruler (which are calibrated in units such that c=1, e.g., seconds and light-seconds). The square lattice of white polka-dots is obtained from them by repeated addition. By assuming that this lattice construction is possible, we are implicitly assuming postulate P2, flatness of spacetime.
The same properties hold for vectors →o2 and →s2, which give the lattice of black dots. As required, the two lattices agree on their 45-degree diagonals. Now within the 10×10 portion of the white lattice shown with gray shading, we have an area of 100. In the same region we count about 100 or 101 black dots — there is some ambiguity because of the dots that lie on the boundary. The density of white and black dots is in fact exactly equal, as can be verified to any desired precision by making the region big enough. In other words, the diagram is drawn so that area is preserved, which is what we are going to show is required. If it was observer 2 rather than 1 who was drawing the diagram, presumably she would choose to draw the black dots in a square lattice and vectors →o2 and →s2 at right angles. This would require vectors →o2 and →s2 to be opened up at an oblique angle and the white lattice to be non-square.
Now suppose we had not made area conserved. What if a region containing 100 white dots had held 200 black ones? Dot-counting is how the observers define area, so if this happened, they would have to agree that a boost by v, from frame 1 to frame 2, doubled the area of the gray region. Because spacetime is flat (P2) and homogeneous (P3), it is possible to take a geometrical shape inscribed in a certain region of spacetime and move, rotate, or flip it. And by isotropy of space (P3), a boost of velocity v is the same as a flip of the spatial dimension followed by a −v boost and another flip. Area is conserved by a flip, so we find that a boost by −v, from frame 2 to frame 1, also doubles area. Thus a +v boost followed by a −v boost would cause a quadrupling of area. But a pair of equal and opposite boosts cancels out, so this is a contradiction. We conclude that if these symmetry principles hold, then spacetime area is the same for any two observers, so it is an invariant.
It may seem unnecessarily clumsy that we’ve used the idea of counting dots in the above argument, but remember that our main use of this result is to derive the form of the metric, and before the metric had been found, we had no system of measurement for relativity, so we had only very primitive techniques at our disposal.


