2.E: Foundations (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Q1
Section 2.5 gives an argument that spacetime area is a relativistic invariant. Is this argument also valid for Galilean relativity?
Q2
Section 2.5 gives an argument that spacetime area is a relativistic invariant.
- Generalize this from 1+1 dimensions to 3+1.
- Use this result to prove that there is no relativistic length con- traction effect along an axis perpendicular to the velocity.
Q3
The purpose of this problem is to find how the direction of a physical object such as a stick changes under a Lorentz transformation. Part b of problem Q2 shows that relativistic length contraction occurs only along the axis parallel to the motion. The generalization of the 1+1 - dimensional Lorentz transformation to 2+1 dimensions therefore consists simply of augmenting equation 1.4.1 in section 1.4 with y′=y. Suppose that a stick, in its own rest frame, has one end with a world-line (τ,0,0) and the other with (τ,p,q), where τ is the stick’s proper time. Call these ends A and B. In other words, we have a stick that goes from the origin to coordinates (p,q) in the (x,y) plane. Apply a Lorentz transformation for a boost with velocity v in the x direction, and find the equations of the world-lines of the ends of the stick in the new (t′,x′,y′)coordinates. According to this new frame’s notion of simultaneity, find the coordinates of B when A is at (t′,x′,y′)=(0,0,0).
- In the special case where q≠0, recover the 1+1 - dimensional result for length contraction given in section 1.3.
- Returning to the general case where q≠0,, consider the angle θ that the stick makes with the x axis, and the related angle θ′ that it makes with the x′ axis in the new frame. Show that tan(θ′)=γtan(θ)
Q4
Section 2.2 discusses the idea that a two-dimensional bug living on the surface of a sphere could tell that its space was curved. Figure 2.2.2 in section 2.2 shows one way of telling, by detecting the path- dependence of parallel transport. A different technique would be to look for violations of the Pythagorean theorem. In the figure 2.E.1 below, 1 is a diagram illustrating the proof of the Pythagorean theorem in Euclid’s Elements (section 2.2/ 2.3). This diagram is equally valid if the page is rolled onto a cylinder, 2, or formed into a wavy corrugated shape, 3. These types of curvature, which can be achieved without tearing or crumpling the surface, are not real to the bug. They are simply side-effects of visualizing its two-dimensional universe as if it were embedded in a hypothetical third dimension — which doesn’t exist in any sense that is empirically verifiable to the bug. Of the curved surfaces in the figure, only the sphere, 4, has curvature that the bug can measure; the diagram can’t be plastered onto the sphere without folding or cutting and pasting. If a two- dimensional being lived on the surface of a cone, would it say that its space was curved, or not? What about a saddle shape?
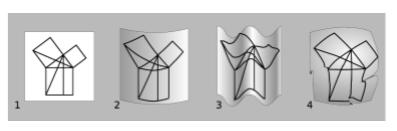
Q5
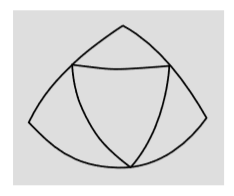
The discrepancy in parallel transport shown in figure 2.2.2 in section 2.2 can also be interpreted as a measure of the triangle’s angular defect d, meaning the amount S−π by which the sum of its interior angles S exceeds the Euclidean value.
- The figure suggests a simple way of verifying that the angular defect of a triangle inscribed on a sphere depends on area. It shows a large equilateral triangle that has been dissected into four smaller triangles, each of which is also approximately equilateral. Prove that D=4d, where D is the angular defect of the large triangle and d the value for one of the four smaller ones.
- Given that the proportionality to area d=kA holds in general, find some triangle on a sphere of radius R whose area and angular defect are easy to calculate, and use it to fix the constant of proportionality k.
Remark: A being who lived on a sphere could measure d and A for some triangle and infer R, which is a measure of curvature. The proportionality of the effect to the area of the triangle also implies that the effects of curvature become negligible on sufficiently small scales. The analogy in relativity is that special relativity is a valid approximation to general relativity in regions of space that are small enough so that spacetime curvature becomes negligible.


