3.E: Kinematics (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Q1
Fred buys a ticket on a spaceship that will accelerate to an ultrarelativistic speed v such that c−v is only 6m/s. Fred was on the track team in high school, so he knows he can run about 8m/s. Once the ship is up to speed, Fred plans to run in the forward direction, thereby becoming the first human to exceed the speed of light. Other than the possible lack of gravity to allow running, what is wrong with Fred’s plan?
Q2
- In the equation vc=v1+v21+v1v2 for combination of velocities, interpret the case where one of the velocities (but not the other) equals the speed of light.
- Interpret the case where the denominator goes to zero.
- Use the geometric series to rewrite the factor \[(tfrac{1}{1+v_1v_2}\), and then expand the expression for vc as a series in v1 and v2, retaining terms up to third order in velocity. How does this relate to the correspondence principle?
Q3
Determine which of the identities in section 3.6 need to be modified in order to be valid in units with c≠1, and describe how they should be modified.
Q4
The Large Hadron Collider accelerates counterrotating beams of protons and collides them head-on. The beam energy has been gradually increased, and the accelerator is designed to reach a maximum energy of 14TeV, corresponding to a rapidity of 10.3.
- Find the velocity of the beam.
- In any collision, the kinetic energy available to do something inelastic (smash up your car, produce nuclear reactions, ...) is the energy in the center of mass frame; in any other frame, there is initial kinetic energy that must also be present in the final state due to conservation of momentum. Suppose that a particular proton in the LHC beam never undergoes a collision with a proton from the opposite beam, and instead is wasted by being dumped into a beamstop. Let’s say that this collision is with a proton in a hydrogen atom left behind by someone’s fingerprint. Find the velocities of the two protons in their common center of mass frame.
Q5
Each GPS satellite is in an orbit with a radius of 26,600km, with an orbital period of half a sidereal day, giving it a velocity of 3.88km/s. The atomic clock aboard such a satellite is tuned to 10.22999999543MHz, which is chosen so that when the satellite is directly overhead, the effect of time dilation (transverse Doppler shift), combined with a general-relativistic effect due to gravity, results in a frequency of exactly 10.23MHz. (GPS started out as a military project, and legend has it that the top brass, suspicious of the crazy relativity stuff, demanded that the satellites be equipped with a software switch to turn off the correction, just in case the physicists were wrong.) There are oscillations superimposed onto these static effects due to the longitudinal Doppler shifts as the satellites approach and recede from a given observer on the ground.
- Calculate the maximum Doppler-shifted frequency for a hypothetical observer in outer space who is being directly approached by the satellite in its orbit.
- In reality, the greatest possible longitudinal component of the velocity is considerably smaller than this due to the geometry. Use the size of the earth to determine this velocity and the corresponding maximum frequency.
Q6
Verify directly, using the geometry of figure below, that for v=3/5, the Doppler shift factor is D=2. (Do not simply plug v=3/5 into the formula D=√1+v1−v.)
Q7
Generalize the numerical calculation of problem Q6 to prove the general result D=√1+v1−v.
Q8
Expand the relativistic equation for the longitudinal Doppler shift of light D(v) in a Taylor series, and find the first two nonvanishing terms. Show that these two terms agree with the nonrelativistic expression, so that any relativistic effect is of higher order in v.
Q9
Prove, as claimed in section 3.5, that we must have a⋅v=0 if the velocity four-vector is to remain properly normalized.
Q10
Example 3.5.1 described the motion of an object having constant proper acceleration a, the world-line being t=1asinhaτ and x=1acoshaτ in a particular observer’s Minkowski coordinates.
- Prove the following results for γ and for the (three-)velocity and (three-)acceleration measured by this observer. \gamma =\cosh a\tau \\ v = \tanh a\tau \\ \text{acceleration} = a\cosh ^{-3}a\tau Do the calculations simply by taking the first and second derivatives of position with respect to time. You will find the following facts helpful: 1-\tanh ^2 = \cosh ^{-2}\\ \frac{\mathrm{d} }{\mathrm{d} x} \tanh = \cosh ^{-2}x
- Interpret the results in the limit of large τ.
Q11
Example 3.5.1 described the motion of an object having constant proper acceleration a, the world-line being t = \frac{1}{a} \sinh a\tau and x = \frac{1}{a} \cosh a\tau in a particular observer’s Minkowski coordinates. Find the corresponding velocity and acceleration four-vectors.
Q12
Starting from the results of problem Q11, repeat problem Q10a using the techniques of section 3.7. You will find it helpful to know that 1-\tanh ^2 = \cosh ^{-2}.
Q13
Let v be a future-directed, properly normalized velocity vector. Compare the value of v\cdot v in the +--- signature used in this book with its value in the signature -+ ++.
Q14
- Prove the relation \frac{\mathrm{d} \gamma }{\mathrm{d} t} = \gamma ^3 a_o\cdot v_o, in the special case where the motion is linear.
- Generalize the result to 3 + 1 dimensions.
Q15
Derive the identity a_o = \frac{1}{(o\cdot v)^2}\left [ P_o a - (o\cdot a)v_a \right ].
Q16
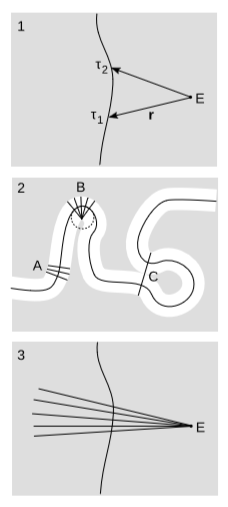
Recapitulating the geometry in figure below, let W be a smooth, timelike world line, E an event not on W, and r the vector from E to a point on W, parametrized by proper time τ. Define the proper distance l between E and a point on W as l^2 = -(P_v r)^2, where the square indicates an inner product of the vector with itself, and the minus sign is because we use the +--- signature. Show that \frac{\mathrm{d} l^2}{\mathrm{d} \tau } = 2(r\cdot v)(r\cdot a)(v\cdot v), where the final factor is just a signature-dependent sign. Does this make sense when W is inertial? Give an example where the derivative vanishes because the first factor is zero, and another example where the second factor is the one that vanishes (but a \neq 0).
Q17
Consider an observer O moving along a world-line W with the constant-acceleration motion defined in Example 3.5.1. In section 3.9, we gave the coordinates of a certain event E that was never “now” as described by our observer. The purpose of this problem is to analyze this is a more elegant and coordinate-invariant way. Let P be a point on W, let B be the event described in section 3.9, and let x = \overrightarrow{BP}, h = \overrightarrow{BE}, and r = \overrightarrow{EP}.
- Show that W, which was originally described in a certain set of coordinates, can instead by defined by the fact that x\cdot v = 0 for every point on W.
- Show that if h is timelike, then r\cdot v is never zero.


