8.1: Rotating Frames of Reference
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Explain rotation and rotating coordinate system
No clock synchronization
Panels 1 and 2 of figure 8.1.1 recapitulate the result of Example 1.4.6. The set of three clocks fixed to the earth in 8.1.1 (1) have been synchronized by Einstein synchronization (Example 1.1.4), i.e., by exchanging flashes of light. The three clocks aboard the moving train, 8.1.1 (2), have been synchronized in the same way, and the events that were simultaneous according to frame 1 are not simultaneous in frame 2. There is a systematic shift in the times, which is represented by the term t′=...−vγx in the Lorentz transformation (Equation 1.4.1).
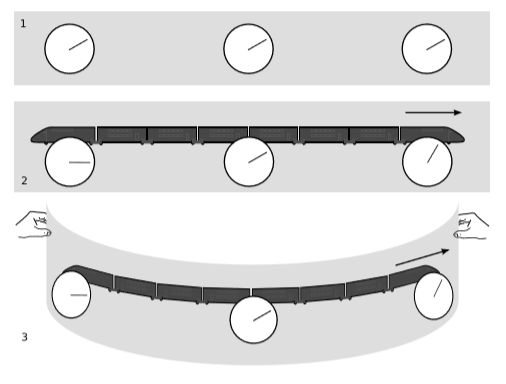
Now suppose we take the diagram of the train and wrap it around, 8.1.1 (3). If we go on and close the loop, making the chain into a circle like a chain necklace, we have a problem. The trend in the clock times can continue until it wraps back around to the beginning, but then there will be a discrepancy.
We conclude that clocks can’t be synchronized in a rotating frame of reference. Such a frame does not admit a universal time coordinate because Einstein synchronization isn’t transitive: synchronizing clock A with clock B, and B with C, does not imply that A is synchronized with C. This nontransitivity is one way of defining what we mean by rotation. That is, if the operational definition of an inertial frame given in section 5.1, shows that our frame is noninertial, and we want to know more about why it’s noninertial, testing for this nontransitivity is a way of finding out whether it’s because of rotation.
Rotation is locally detectable
The people aboard the circular train know that their attempts at synchronization fail, so they can tell, without reference to anything external, that they’re going in a circle.
Although this is a book on special, not general, relativity, it’s interesting to note the following possibility. Suppose that we verify, by local experiments, that we have a good, nonrotating, inertial frame of reference. It is then imaginable that if we view distant galaxies from this frame, we will see them rotate at some angular frequency Ω about some axis on the celestial sphere. If this is observed, then we must infer that it is the universe as a whole — not our laboratory! — that is rotating. Such an effect has been searched for, and, for example, an upper limit \Omega \lesssim 10^{-7} radian/year was inferred by Clemence.1 General-relativistic models of such rotating cosmologies have a preferred vector constituting the direction of the axis about which matter rotates, but there is no global center of rotation. Current upper limits on Ω are good enough to rule out any significant effect on cosmological expansion due to centrifugal forces.
The Sagnac effect
Although the train scenario is obviously unrealistic, the time shift is far from hypothetical. This type of effect, called the Sagnac effect, was first observed by M. Georges Sagnac in 1913, and it relates to the principle of the ring laser gyroscope (Example 1.1.4), used in passenger jets. (The name is French, and is pronounced \sah-NYAHK.") To find the Sagnac effect quantitatively, we note that in the circular train example (ignoring signs) the relevant term in the Lorentz transformation, v\gamma x, would accumulate, after one complete circuit of Einstein synchronization, a discrepancy \delta equal to the circumference of the circle multiplied by v\gamma. If the circle's radius is r and the angular velocity \omega, we have \Delta t = 2\pi \gamma r^2\omega. This can be rewritten in terms of the circle's area A as \Delta t = 2A\omega, or, reinserting factors of c to accomodate SI units, \Delta t = \frac{2A\omega }{c^2}. The proportionality to the enclosed area is not an accident; the product vx has the form of the integrand F\cdot ds occurring in Stokes' theorem.
Example \PageIndex{1}: Sagnac effect in the Hafele-Keating experiment
A clock at the equator of the earth rotates at a frequency ω of 2π radians per sidereal day, suffering a Sagnac effect of 210\: ns per day. The traveling atomic clocks in the Hafele-Keating experiment went around the world in both directions, and were compared with a third set of clocks that stayed in Washington,DC. Since the time required to fly around the earth was also on the order of one day, the differences in the values of ω for the three sets of clocks were on the same order of magnitude as the ω of the earth, and we therefore expect cumulative differential Sagnac effects that are also on the order of a hundred nano seconds. These effects exist only in the rotating frame of the earth, but the things being measured are proper times, and proper time is a scalar, so the experimental results are independent of what frame of reference is used for calculating them. Since the airline pilots provided Hafele and Keating with navigational data referred to the rotating earth, they analyzed their results in the rotating frame, in which there was a Sagnac effect. They could equally well have transformed their data into the frame of the stars, in which case the same result would have been predicted, but it would have been described as arising from kinematic time dilation.
Example \PageIndex{2}: Ring laser gyroscope
The ring laser gyroscope in the photo in Example 1.1.4 looks like it has an area on the order of 10^2\: cm^2 and uses red light. For use in navigation, one wants to be able to detect a change in course of, say, one degree in our hour, or ω ∼5×10^{-6}\: radian/s. The result is a time shift ∆t ∼ 10^{-24}\: s, which for red light is a phase shift of only ∆φ = 4πAω/cλ ∼3×10^{-9} radian. In the original nineteenth-century experiments, this phase shift would have had to be measured by producing interference between the two beams and measuring the change in intensity resulting from this change in phase. Our estimate of φ shows that this is impractical for a portable instrument. In a modern ring laser gyroscope, an active laser medium is inserted in the loop, and the result is that the loop resonates at a frequency that is shifted from the laser’s natural frequency by ∆f ∼ ∆φc/L, where L is the circumference. The result is a frequency shift of a few Hz, which is easily measurable. An alternative technique, used in the fiber optic gyroscope, is to wrap N turns of optical fiber around the circumference, effectively changing A to NA.
A rotating coordinate system
The GPS system is a practical example of a case where we naturally want to employ a rotating coordinate system. Hikers and sailors, after all, want to know where they are relative to the earth’s rotating surface. Since locations need to be determined to within meters, the timing of signals needs to be done to a precision of something like (1 m)/c, which is a few nanoseconds. This is why the GPS satellites have atomic clocks aboard, and timing to this precision clearly requires that relativistic effects be taken into account. We therefore need not a rotating Newtonian coordinate system but a rotating relativistic one. Let’s start with the nonrotating frame, and define coordinates (t,r,θ,z), with the spatial part (r,θ,z) being ordinary cylindrical coordinates. For simplicity, we’ll neglect the z coordinate in what follows. Extending the result of problem Q1 in chapter 7 from 2 + 0 dimensions to 2 + 1, we have the metric
ds^2 = dt^2 - dr^2 - r^2 d\theta ^2
The results above show that we do not expect to be able to define a completely satisfactory time coordinate in the rotating frame, so let’s start with the minimal change (t,r,θ) → (t,r,θ'), where θ' = θ - ωt. This is at least enough to make world-lines of constant θ' be ones that revolve around the origin at the appropriate frequency. Substituting dθ = dθ' + ω dt, we find
ds^2 = (1 - \omega ^2r^2)dt^2 - dr^2 - r^2 d\theta '^2 - 2\omega r^2 d\theta 'dt
Recognizing ωr as the velocity of one frame relative to another, and (1 - ω^2r^2) {-1/2} as γ, we see that we do have a relativistic time dilation effect in the dt^2 term. But the dr^2 and dθ'^2 terms look the same as in Equation \PageIndex{1}. Why don’t we see any Lorentz contraction of the length scale in the azimuthal direction?
The answer is that coordinates in relativity are arbitrary, and just because we can write down a certain set of coordinates, that doesn’t mean they have any special physical interpretation. The coordinates (t,r,θ') do not correspond physically to the quantities that a rotating observer R would measure with clocks and meter-sticks. If R uses a ruler to measure a short arc along the circumference of the circle r = r', the distance is a distance being measured between events in spacetime that are simultaneous in the rest frame of the ruler, and these do not occur at the time value of the time coordinate t. In the Lorentz transformation, for linear motion, it is the -vγx term applied to the times that fixes this problems and makes t0 properly represent simultaneity in the new frame. In our rotational version, we could try to do something similar by defining a time coordinate t' = t + fθ', where f is a function of r that is engineered so that the dθ'dt cross term in the metric would go away. This can be done (the function f that works turns out to be ωr^2/(1 - ω^2r^2)), but the problem is that the t' coordinate is not single-valued, in the sense that (t,r,θ) and (t,r,θ + 2π) would not produce the same t'. This is inevitable, as we’ve seen in in the beginning of this section, so we can’t improve on the coordinates (t,r,θ') and the metric (Equation \PageIndex{2}).
The coordinates (t,r,θ'), with the metric (Equation \PageIndex{2}) are the ones used in the GPS system, and in that context are called Earth-Centered Inertial (ECI) coordinates. (Another name is Born coordinates.) Their time coordinate is not the time measured by a clock in the rotating frame but is simply the time coordinate of the nonrotating frame of reference tied to the earth’s center. Conceptually, we can imagine this time coordinate as one that is established by sending out an electromagnetic “tick-tock” signal from the earth’s center, with each satellite correcting the phase of the signal based on the propagation time inferred from its own r. In reality, this is accomplished by communication with a master control station in Colorado Springs, which communicates with the satellites via relays at Kwajalein, Ascension Island, Diego Garcia, and Cape Canaveral.


