10.2: Fields in Relativity
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Explain why Coulomb’s law cannot be extended to include magnetism
Based on what we learned in section 10.1, the next natural step would seem to be to find some way of extending Coulomb’s law to include magnetism. For example, we could try to find a formula for the magnetic force between charges q1 and q2 based on not just their relative positions but also on their velocities. The following considerations, however, tell us not to go down that path.
Time delays in Forces Exerted at a Distance
Relativity forbids Newton’s instantaneous action at a distance. Since forces can’t be transmitted instantaneously, it becomes natural to imagine force-effects spreading outward from their source like ripples on a pond, and we then have no choice but to impute some physical reality to these ripples. We call them fields, and they have their own independent existence.
Even empty space, then, is not perfectly featureless. It has measurable properties. For example, we can drop a rock in order to measure the direction of the gravitational field, or use a magnetic compass to find the direction of the magnetic field. This concept made a deep impression on Einstein as a child. He recalled that as a five-year-old, the gift of a magnetic compass convinced him that there was “something behind things, something deeply hidden.”
Fields Carry Energy
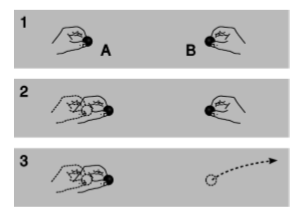
The smoking-gun argument for this strange notion of traveling force ripples comes from the fact that they carry energy. In figure 10.2.1 (1), Alice and Betty hold positive charges A and B at some distance from one another. If Alice chooses to move her charge closer to Betty’s, figure 10.2.1 (2), Alice will have to do some mechanical work against the electrical repulsion, burning off some of the calories from that chocolate cheesecake she had at lunch. This reduction in her body’s chemical energy is offset by a corresponding increase in the electrical potential energy q∆V. Not only that, but Alice feels the resistance stiffen as the charges get closer together and the repulsion strengthens. She has to do a little extra work, but this is all properly accounted for in the electrical potential energy.
But now suppose, figure 10.2.1 (3), that Betty decides to play a trick on Alice by tossing charge B far away just as Alice is getting ready to move charge A. We have already established that Alice can’t feel charge B’s motion instantaneously, so the electric forces must actually be propagated by an electric field. Of course this experiment is utterly impractical, but suppose for the sake of argument that the time it takes the change in the electric field to propagate across the diagram is long enough so that Alice can complete her motion before she feels the effect of B’s disappearance. She is still getting stale information about B’s position. As she moves A to the right, she feels a repulsion, because the field in her region of space is still the field caused by B in its old position. She has burned some chocolate cheesecake calories, and it appears that conservation of energy has been violated, because these calories can’t be properly accounted for by any interaction with B, which is long gone.
If we hope to preserve the law of conservation of energy, then the only possible conclusion is that the electric field itself carries away the cheesecake energy. In fact, this example represents an impractical method of transmitting radio waves. Alice does work on charge A, and that energy goes into the radio waves. Even if B had never existed, the radio waves would still have carried energy, and Alice would still have had to do work in order to create them.
Fields must have transformation laws
In the foregoing discussion I’ve been guilty of making arguments that fields were “real.” Sorry. In physics, and particularly in relativity, it’s usually a waste of time worrying about whether some effect such as length contraction is “real” or only “seems that way.” But thinking of fields as having an independent existence does lead to a useful guiding principle, which is that fields must have transformation laws. Suppose that at a certain location, observer o1 measures every possible field — electric, magnetic, bodice-ripper-sexual-attractional, and so on. (The gravitational field is not on the list, for the reasons discussed in section 5.2.) Observer o2, passing by the same event but in a different state of motion, could carry out similar measurements. We’re talking about measurements being carried out on a cubic inch of pure vacuum, but suppose that the answer to Peggy Lee’s famous question is “Yes, that’s all there is” — the only information there is to know about that empty parcel of nothingness is the (frame-dependent) value of the fields it contains. Then o1 ought to be able to predict the results of o2’s measurements. For if not, then what is the nature of the information that is hidden from o1 but revealed to o2? Presumably this would be something related to how the fields were produced by certain particles long ago and far away. For example, maybe o1 is at rest relative to a certain charge q that helped to create the fields, but o2 isn’t, so o2 picks up q’s magnetic field, which is information unavailable to o1 — who thinks q was at rest, and therefore didn’t make any magnetic field. This would contradict our “that’s all there is” hypothesis.
To show the power of “that’s all there is,” consider example 9.1.1, in which we found that boosting a solenoid along its own axis doesn’t change its internal field. As a fact about solenoids, it’s fairly obscure and useless. But if the fields must have transformation laws, then we’ve learned something much more general: a magnetic field always stays the same under a boost in the direction of the field.


