10.4: Transformation of the Fields
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Explain the following laws within the Ideal Gas Law
Since we have associated the components of the electric and magnetic fields with elements of a rank-2 tensor, the transformation law for these fields now follows from the general tensor transformation law for rank-2 tensors (section 9.2). We first state the general rule, in a prettified form, and then give some concrete examples. Under a boost by a three-velocity \vec{v}, the electric and magnetic fields \vec{E} and \vec{B} transform to \vec{E}' and \vec{B}' according to these rules:
Example \PageIndex{1}: A line of charge
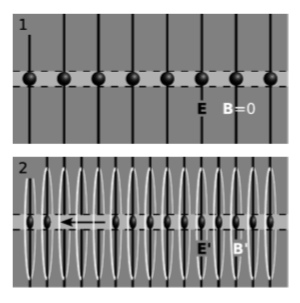
Figure \PageIndex{1} (1) shows a line of charges. At a given nearby point, it creates an electric field E that points outward, as measured by an observer o who is at rest relative to the charges. This field is represented in the figure by its pattern of field lines, which start on the charges and radiate outward like the bristles of a bottle brush. Because the charges are at rest, the magnetic field is zero. (Finding the magnitude of the field at a certain distance is a straightforward application of Gauss’s law.)
Now consider an observer o', figure \PageIndex{1} (2), moving at velocity v to the right relative to o. Without even worrying about how the field was created, we can transform the fields, at the point in space discussed previously, into the new frame. The result is E' = γE and B'_⊥ = -γv × E. In this frame, the electric field is more intense, and there is also a magnetic field, whose pattern of white field lines forms circles lying in planes perpendicular to the line. If we do happen to know that the field was created created by the line of charge, which is moving according to o', then we can explain these results as arising from two effects. First, the line of charge has been length-contracted. This causes the density of charge per unit length to increase by a factor of γ, with a proportional increase in the electric field. In the field-line description, we simply have more charges in the figure, so there are more field lines coming out of them. Second, the line of charge is moving to the left in this frame, so it forms an electric current, and this current is the cause of the magnetic field B'.
Example \PageIndex{2}: A moving charge
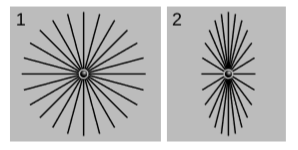
Figure \PageIndex{2} (1) shows the electric field lines of a charge, in the charge’s rest frame K. In figure \PageIndex{2} (2)we see the same electric field, in a frame K' in which the charge is moving along the x-axis, which points to the right, at 90\% of c. (In this frame there is also a magnetic field, which is not shown.) This electric field, which is time-varying, is shown as a snapshot in a hyperplane of simultaneity t' = 0 of K'. Surprisingly, these field lines all point toward the charge’s present position in K'.
Disturbances in the electromagnetic field propagate at c, not instantaneously, so one might have expected the field at a certain location P in this figure to point toward a location at a distance r that the charge had occupied at an earlier time t' = -r/c. This would have produced a set of curved field lines reminiscent of the wake of a boat. To see that this is not possible, consider the point (0, 0, h, 0) in the Minkowski coordinates of K, i.e., a point on the y-axis. After a Lorentz transformation along x, the coordinates of this point in K' are still (0, 0, h, 0), so in K' as well it lies on a line that passes transversely through the present position of the charge. Since this point has E_x = 0 and \vec{B} = 0 in K, application of the transformation laws shows that E'_x = 0 as well, so that the field points toward the charge’s present position, not its past position.
A similar but more complicated calculation shows that the field at intermediate angles is also in the instantaneously radial direction. Rather than filling in the details, we note that this makes sense because the Poynting vector \vec{E} × \vec{B} then has no radial component, which is as expected because energy should be transported forward but not radiated outward.
One might worry that this would indicate that the information about the charge’s position was propagating instantaneously, contradicting relativity. But this is a charge that has always been in its current state of motion and always will be. If the charge’s motion had been disturbed by some external force at a time later than t' = -r/c, the field lines in K would still be pointing toward the location that the charge had previously occupied while at rest, and the field in K' would be pointing toward its linearly extrapolated position.
Example \PageIndex{3}: A field behaving like a stick
Figure \PageIndex{2} (2) appears identical to a copy of figure \PageIndex{2} (1) that has been Lorentz contracted by 1/γ, and we can verify from the transformation laws for the fields that this is correct. Since these transformation laws apply regardless of how the fields were produced, we have a general rule, which is that if a field is purely electric in one frame, then its direction transforms to another frame in the same way as the direction of a stick, when we transform out of the stick’s rest frame.
It is not true in general that electric field lines can simply be carried over from one frame to another as if we were Lorentz contracting a rat’s nest built out of wire. This property holds only when the original frame is of a very special kind: a frame in which the field is purely electric. (We can always find such a frame if E^2 > B^2; see section 10.5.) As a counterexample to the notion that it applies more generally, consider the case in which a field is purely magnetic in a certain frame. Then the electric field lines do not even exist in the original frame, but do exist in the new one.
Coming back to the case where the original field is purely electric, so that the stick-like behavior does hold, it is not immediately obvious why there should be this strange correspondence between sticks and field lines. The methods used in problem Q3 of chapter 2 do not seem to have much in common with the ones we have used to determine how the electric field behaves. But the following physical argument shows that there is a simple reason for the identical behavior.
Consider a stick with charges +q and -q fixed at the ends. The stick is nonrotating and moving inertially. In the stick’s rest frame K, there is a field line originating from +q and terminating on -q which coincides with the stick. Now consider frame K' moving in some direction relative to the stick. As discussed in example 10.4.2, the field due to each charge points toward or away from its present instantaneous position in K' as well as K. Therefore each field, at the stick, is parallel to the stick, and we again have a field line in K' that coincides with the stick. Since the transformation of the field is independent of how the field was created, this holds for any field that is purely electric in the original frame.


