10.6: Stress-energy tensor of the electromagnetic field

Learning Objectives

• Explain the stress-energy tensor for electromagnetic field

The electromagnetic field has a stress-energy tensor associated with it. From our study of electromagnetism we know that the electromagnetic field has energy density \(U=(E^2+B^2)/8\pi k\) and momentum density \(\vec{S}=(\vec{E}\times\vec{B})/4\pi k\) (in units where \(c=1\), with \(k\) being the Coulomb constant). This fixes the components of the stress-energy tensor of the form \(T^{t\ldots}\) and \(T^{\ldots t}\), i.e., the top row and left column, to look like this:

\[T^{\mu\nu} = \begin{pmatrix} U & S_x & S_y & S_z \\ S_x & & & \\ S_y & & & \\ S_z & & & \end{pmatrix}\]

Figure \(\PageIndex{1}\): Pressure and tension in electrostatic fields.

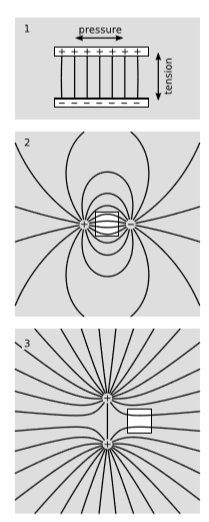
The following argument tells us something about what to expect for the components \(T^{xx}\), \(T^{yy}\), and \(T^{zz}\), which are interpreted as pressures or tensions, depending on their signs. In figure \(\PageIndex{1}\) (1), the capacitor plates want to collapse against each other in the vertical (\(y\)) direction, but at the same time the internal repulsions within each plate make that plate want to expand in the \(x\) direction. If the capacitor is built out of materials that hold their shape, then the electromagnetic tension in \(T^{yy}<0\) is counteracted by pressure \(T^{yy}>0\) in the materials, while the electromagnetic pressure \(T^{xx}>0\) is canceled by the materials’ tension \(T^{xx}<0\). We got these results for a particular physical situation, but relativity requires that the stress-energy be defined at every point based on the fields at that point, so our conclusions must hold generally. In figure \(\PageIndex{1}\) (2) and figure \(\PageIndex{1}\) (3), white boxes have been drawn in regions where the total field is strong and the fields are strongly interacting. In figure \(\PageIndex{1}\) (2), there is tension in the \(x\) direction and pressure in \(y\); the tension can be thought of as contributing to the attraction between the opposite charges. In 3, there is also \(x\) tension and \(y\) pressure; the pressure contributes to the like charges’ repulsion.

To make this more quantitative, consider the discontinuity in \(E_y\) at the upper plate in figure \(\PageIndex{1}\) (1). The field abruptly switches from \(0\) on the outside to some value \(E\) between the plates. By Gauss’s law, the charge per unit area on the plate must be \(\sigma=E/4\pi k\). The average field experienced by the charge in the plate is \(\overline{E}=(0+E)/2=E/2\), so the force per unit area, i.e., the tension in the field, is \(\sigma \overline{E}=E^2/8\pi k\). Thus we expect \(T^{yy}=-E^2/8\pi k\) if \(E\) is along the \(y\) axis.

For the reader who wants the full derivation of the remaining nine components of the tensor, we now give an argument that makes use of the following list of its properties. Other readers can skip ahead to where the full tensor is presented.

1. \(T\) is symmetric, \(T^{µν} = T^{νµ}\).
2. The components must be second-order in the fields, e.g., we can have terms like \(E_xB_z\), but not \(E_{x}^{3} B_{z}^{7}\) or \(E_xB_zB_y\). This is because Maxwell’s equations are linear, and when a wave equation is perfectly linear, the corresponding energy expression is second-order in the amplitude of the wave.
3. \(T\) has the parity properties described in Example 9.2.3.
4. The electric and magnetic fields are treated symmetrically in Maxwell’s equations, so they should be treated symmetrically in the stress-energy tensor. E.g., we could have a term like \(7E_{x}^{2} + 7B_{z}^{2}\), but not \(7E_{x}^{2} + 6B_{z}^{2}\).
5. In section 9.2, we saw that the trace energy condition \(T^a\: _a \geq 0\) is satisfied by a cloud of dust if and only if the dust’s mass-energy is not transported at a speed greater than \(c\). In section 4.1, we saw that all ultrarelativistic particles have the same mechanical properties. Since a cloud of dust, in the limit where its speed approaches \(c\), is on the edge of the bound set by the trace energy condition, \(T^a\: _a \rightarrow 0\), we expect that the electromagnetic field, in which disturbances propagate at \(c\), should also exactly saturate the trace energy condition, so that \(T^a\: _a = 0\).
6. The stress-energy tensor should behave properly under rotations, which basically means that \(x\), \(y\), and \(z\) should be treated symmetrically.
7. An electromagnetic plane wave propagating in the \(x\) direction should not exert any pressure in the \(y\) or \(z\) directions.
8. If the field obeys Maxwell’s equations, then the energy-conservation condition \(\frac{\partial T^{ab}}{\partial x^a} = 0\) should hold.

These facts are enough to completely determine the form of the remaining nine components of the stress-energy tensor. Property 3 requires that all of these components be even under parity. Since electric fields flip under parity but magnetic fields don’t ( Example 10.3.1), these components can only have terms like \(E_i E_j\) and \(B_i B_j\), not mixed terms like \(E_i B_j\). Taking into account properties 4 and 6, we find that the diagonal terms must look like

and the off-diagonal ones

Property 5 gives \(1/2-a-3b=0\) and 7 gives \(b=-a/2\), so we have \(a=-1\) and \(b=1/2\). The determination of \(c=-1\) is left as an exercise, problem Q4.

We have now established the complete expression for the stress-energy tensor of the electromagnetic field, which is

where

and \(\sigma\), known as the Maxwell stress tensor, is given by

All of this can be expressed more compactly and in a coordinate-independent way as

\[T^{ab} = \frac{1}{4\pi k} \left(\mathcal{F}^{ac}\mathcal{F}^b\: _c + \frac{1}{4}o^do_dg^{ab}\mathcal{F}_{ef}\mathcal{F}^{ef}\right)\]

where \(\vec{o}\) is a future-directed velocity vector, so that \(o^do_d=+1\) for the signature \(+---\) used in this book, and \(-1\) if the signature is \(-+++\).

Example \(\PageIndex{1}\): Stress-energy tensor of a plane wave

Let an electromagnetic plane wave (not necessarily sinusoidal) propagate along the \(x\)-axis, with its polarization such that \(\vec{E}\) is in the \(y\) direction and \(\vec{B}\) on the \(z\) axis, and \(|\vec{E}| = |\vec{B}| = A\). Then we have the following for the stress-energy tensor.

\[T^{\mu \nu } = \frac{A^2}{4\pi k} \begin{pmatrix} 1 & 1 & 0 & 0\\ 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix}\]

The \(T^{tt}\) component tells us that the wave has a certain energy density. Because the wave is massless, we have \(E^2 - p^2 = m^2 = 0\), so the momentum density is the same as the energy density, and \(T^{tx}\) is the same as \(T^{tt}\). If this wave strikes a surface in the \(yz\) plane, the momentum the surface absorbs from the wave will be felt as a pressure, represented by \(T^{xx}\).

In the ultrarelativistic limit \(v →1\), this becomes

\[T^{\mu \nu } = \text{(energy density)} \times \begin{pmatrix} 1 & 1 & 0 & 0\\ 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix}\]

which is exactly the same as the result for our electromagnetic wave. This illustrates the fact discussed in section 4.1 that all ultrarelativistic particles have the same mechanical properties.

Example \(\PageIndex{2}\): Mass of a capacitor

Figure \(\PageIndex{2}\): Mass of a capacitor.

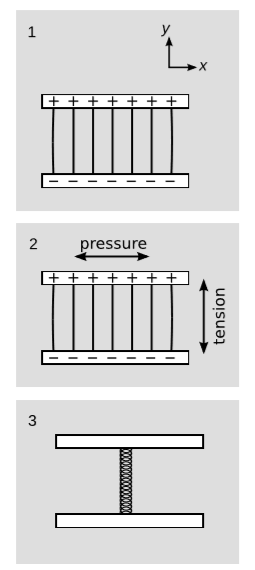
Consider the mass of a charged parallel-plate capacitor, figure \(\PageIndex{2}\) (1), first in its rest frame and then in a frame boosted in the direction parallel to the field (perpendicular to the plates). If we’re not careful, we run into the following paradox. Under a boost, an electric field parallel to the boost remains unchanged. Therefore in the boosted frame, we have exactly the same field strength, but filling a volume that has been decreased by length contraction. Therefore the mass-energy of the capacitor is greatest in its own rest frame, which is absurd and would contradict our proof in section 9.3 that the energy-momentum of an isolated system transforms as a four-vector.

There solution of the paradox comes from recognizing that we assumed the capacitor to be in static equilibrium, but we ignored the stress-energy of whatever mechanical supports were maintaining this equilibrium. If we consider only the stress-energy \(T_{(em)}\) of the electromagnetic field, then we have \(T_{(em)}^{tt} = \frac{1}{8\pi k}E^2\) (energy density) and \(T_{(em)}^{yy} = -\frac{1}{8\pi k}E^2\) (tension in the \(y\) direction, parallel to the field), figure \(\PageIndex{2}\) (2). It’s easy to see that this has a nonvanishing divergence, since \(\partial _y T_{(em)}^{yy} \neq 0\) at the plates, and there are no other terms in the stress-energy tensor that could compensate for this.

There is nothing surprising here; only the total stress-energy tensor \(T\) has to be divergenceless, not \(T_{(em)}\). It would violate the laws of physics if the capacitor were to remain in equilibrium like this without some force to counter the electromagnetic tension. Let’s say that this force is provided by a spring, as in figure \(\PageIndex{2}\) (3). The spring has its own contribution \(T_{(s)}\) to the stress-energy. For convenience, let’s imagine making the spring filled in (rather than a hollow cylinder) and fattening it up so that it fills the entire interior volume of the capacitor. Then to achieve static equilibrium in the rest frame, we need the pressure in the spring to cancel out the pressure in the electric field. We therefore have \(T^{yy} = 0\) for the total stress-energy tensor.

If we now apply the tensor transformation law to the stress-energy tensor, we find that the stress-energy tensor in the boosted frame contains a mass-energy density \(T^{t't'}\) that depends only on \(T^{tt}\) and \(T^{yy}\). (There also has to be an \(xx\) component to keep the plates from exploding laterally, but that doesn’t enter here.) But we have \(T^{yy} = 0\), so the problem is exactly the same as transforming a lump of nonrelativistic matter, and we know that that calculation comes out OK. For an explicit demonstration that this still works out if we drop the simplifying assumption that the spring fills the entire interior volume of the capacitor, see Rindler and Denur, “A simple relativistic paradox about electrostatic energy,” Am J Phys 56 (1988) 9.