8.S: Collide. Create. Annihilate. (Summary)

mass: the magnitude of the 4 -vector called momenergy

"Mass can be converted into energy and energy can be converted into mass" - this is a loose and sometimes misleading way to summarize some consequences of the two principles that are basic and really accurate: (1) The total momenergy of an isolated system of particles remains unchanged in a reaction; (2) The invariant magnitude of the momenergy of any given particle equals the mass of that particle.

How much sound information about physics can be extracted from these basic principles? What troubles sometimes arise from accepting a too loose formulation of the "principle of equivalence of mass and energy"? Some answers to these questions appear in the dialog that follows, which serves also as a summary of this chapter.

DIALOG: USE AND ABUSE OF THE CONCEPT OF MASS

Does an isolated system have the same mass as observed in every inertial (free-float) reference frame?	Yes. Given in terms of energy \(E\) and momentum \(p\) by \(m^{2}=E^{2}-p^{2}\) in one frame, by \(m^{2}=\left(E^{\prime}\right)^{2}-\) \(\left(p^{\prime}\right)^{2}\) in another frame. Mass of an isolated system is thus an invariant.
Does its energy have the same value in every inertial frame?	No. Energy is given by \(E=\left(m^{2}+p^{2}\right)^{1 / 2}\) or \[E=m /\left(1-v^{2}\right)^{1 / 2}\] or \[E=(\text { mass })+(\text { kinetic energy })=m+K\] Value depends on the frame of reference from which the particle (or isolated system of particles) is observed. Value is lowest in the frame of reference in which the particle (or system) has zero momentum (zero total momentum in the case of an isolated system of particles). In that frame, and in that frame only, energy equals mass.
Does energy equal zero for an object of zero mass, such as a photon or neutrino or graviton?	No. Energy has value \(E=\left(0^{2}+p^{2}\right)^{1 / 2}=p\) (or in conventional units \(E_{\text {conv }}=c p_{\text {conv }}\) ). Alternatively one can say - formally - that the entire energy resides in the form of kinetic energy \((K=p\) in this special case of zero mass), none at all in the form of rest energy. Thus, \[E=(\text { mass })+(\text { kinetic energy })=0+K=K=p\] (case of zero mass only!).
Can a photon - that has no mass - give mass to an absorber?	Yes. Light with energy \(E\) transfers mass \(m=E(=\) \(E_{\text {conv }} / c^{2}\) ) to a heavy absorber (Exercise 8.5).
Invariance of mass: Is that feature of nature the same as the principle that all electrons in the universe have the same mass?	No. It is true that all elementary particles of the same kind have the same mass. However, that is a fact totally distinct from the principle that the mass of an isolated system has identical value in whatever free-float frame it is figured (invariance of system mass).
Invariance of mass: Is that the same idea as the conservation of the momenergy of an isolated system?	No. Conservation of momenergy - the principle conservation of the momenergy of an isolated sysvalid for an isolated system - says that the momentem? ergy 4-vector figured before the constituents of a system have interacted is identical to the momenergy 4-vector figured after the constituents have interacted. In contrast, invariance of mass-the magnitude of the momenergy 4-vector - says that that mass is the same in whatever free-float frame it is figured.
Momenergy: Is that a richer concept than mass?	Yes. Momenergy 4-vector reveals mass and more: the motion of object or system with the mass
Conservation of the momenergy of an isolated system: Does this imply that collisions and interactions within an isolated system cannot change the system’s mass?	Yes. Mass of an isolated system, being the magnitude of its momenergy 4-vector, can never change (as long as the system remains isolated).
Conservation of the momenergy of an isolated system: Does this say that the constituents that enter a collision are necessarily the same in individual mass and in number as the constituents that leave that collision?	No! The constituents often change in a high-speed encounter. Example 1: Collision of two balls of putty that stick together - after collision hotter and therefore very slightly more massive than before. Example 2: Collision of two electrons \(\left(e^{-}\right)\)with sufficient violence to create additional mass, a pair consisting of one ordinary electron and one positive electron (positron: \(e^{+}\)): \[e^{-}(\text {fast })+e^{-}(\text {at rest }) \rightarrow e^{+}+3 e^{-}\] Example 3: Collision that radiates one or more photons: \[\begin{array}{r} e^{-}(\text {fast })+e^{-}(\text {at rest }) \rightarrow \\ 2\left(\begin{array}{c} \text { electrons of } \\ \text { intermediate } \\ \text { speed } \end{array}\right)+\left(\begin{array}{c} \text { electromagnetic } \\ \text { energy (photons) } \\ \text { emitted in the } \\ \text { collision process } \end{array}\right) \end{array}\] In all three examples the system momenergy and system mass are each the same before as after.
Can I figure the mass of an isolated system composed of a number, \(n\), of freely-moving objects by simply adding the masses of the individual objects? Example: Collection of fast-moving molecules.	Ordinarily NO, but yes in one very special case: Two noninteracting objects move freely and in step, side by side. Then the mass of the system does equal the sum of the two individual masses. In the general case, where the system parts are moving relative to each other, the relation between system mass and mass of parts is not additive. The length, in the sense of interval, of the 4-vector of total momenergy is not equal to the sum of the lengths of the individual momenergy 4-vectors, and for a simple reason: In the general case those vectors do not point in the same spacetime direction. Energy however, does add and momentum does add: \[E_{\text {system }}=\sum_{i=1}^{n} E_{i} \quad \text { and } \quad p_{x, \text { system }}=\sum_{i=1}^{n} p_{x, i}\] From these sums the mass of the system can be evaluated: \[M_{\text {system }}^{2}=E_{\text {system }}^{2}-p_{x, \text { system }}^{2}-p_{y, \text { system }}^{2}-p_{z, \text { system }}^{2}\]
Can we simplify this expression for the mass of an isolated system composed of freely moving objects when we observe it from a free-float frame so chosen as to make the total momentum be zero?	Yes. In this case the mass of the system has a value given by the sum of energies of individual particles: \[M_{\text {system }}=E_{\text {system }}=\sum_{i=1}^{n} E_{i}\] [in zero-total mentum frame] Moreover, the energy of each particle can always be exp \(K:\) \[E_{i}=m_{i}+K_{i} \quad(i=1,2,3, \ldots, n)\] So the mass of the system exceeds the sum of the masses of its individual particles by an amount equal to the total kinetic energy of all particles (but only as observed in the frame in which total momentum equals zero): \[M_{\text {system }}=\sum_{i=1}^{n} m_{i}+\sum_{i=1}^{n} K_{i}\] [in zero-total [in entum frame] For slow particles (Newtonian low-velocity limit) For slow particles (Newtonian low-velocity limit) the kinetic energy term is negligible compared to the the kinetic energy term is negligible compared to the mass term. So it is natural that for years many thought that the mass of a system is the sum of the masses of its parts. However, such a belief leads to matter of principle at all velocities.
What’s the meaning of mass for a system in which the particles interact as well as move?	The energies of interaction have to be taken into account. They therefore contribute to the total energy, \(E_{\text {system }}\), that gives the mass \[M_{\text {system }}=\left(E_{\text {system }}^{2}-p_{\text {system }}^{2}\right)^{1 / 2}\]
How do we find out the mass of a system of particles	Weigh it! Weigh it by conventional means if we are (Table 8.1) that are held - or stick - together?
Does mass measure "amount of matter"?	Nature does not offer us any such concept as "’amount of matter." History has struck down every proposal to define such a term. Even if we could count number of atoms or by any other counting method try to evaluate amount of matter, that number would not equal mass. First, mass of the specimen changes with its temperature. Second, atoms tightly bonded in a solid weigh less - are less massive - than the same atoms free. Third, many of nature’s atoms undergo radioactive decay, with still greater changes of mass. Moreover, around us occasionally, and continually in stars, the number of atoms and number of particles themselves undergo change. How then speak honestly? Mass, yes; "’amount of matter," no.
Does the explosion in space of a 20-megaton hydrogen bomb convert \(0.93\) kilogram of mass into energy (fusion, Section 8.7)? \(\left[\Delta m=\Delta E_{\text {rest, conv }} / c^{2}=\right.\) \(\left(20 \times 10^{6}\right.\) tons TNT) \(\times\left(10^{6}\right.\) grams \(/\) ton \() \times\left(10^{3}\right.\) calories/gram of "TNT equivalent") X (4.18 joules/calorie \() / c^{2}=\left(8.36 \times 10^{16}\right.\) joules \() /(9 \times\) \(10^{16}\) meters \(^{2} /\) second \(\left.^{2}\right)=0.93\) kilogram]	Yes and no! The question needs to be stated more carefully. Mass of the system of expanding gases, fragments, and radiation has the same value immediately after explosion as before; mass \(M\) of the system has not changed. However, hydrogen has been transmuted to helium and other nuclear transformations have taken place. In consequence the makeup of mass of the system \[M_{\text {sssem }}=\sum_{i=1}^{n} m_{i}+\sum_{i=1}^{n} K_{i}\] [in zero-total momentum frame] has changed. The first term on the right-sum of masses of individual constituents - has decreased by \(0.93\) kilogram: \[\left(\sum_{i=1}^{n} m_{i}\right)_{\text {after }}=\left(\sum_{i=1}^{n} m_{i}\right)_{\text {before }}-0.93 \text { kilogram }\] The second term - sum of kinetic energies, including "kinetic energy" of photons and neutrinos produced - has increased by the same amount: \[\left(\sum_{i=1}^{n} K_{i}\right)_{\text {after }}=\left(\sum_{i=1}^{n} K_{i}\right)_{\text {before }}+0.93 \text { kilogram }\] The first term on the right side of this equation the original heat content of the bomb - is practically zero by comparison with \(0.93\) kilogram. Thus part of the mass of constituents has been converted into energy; but the mass of the system has not changed.
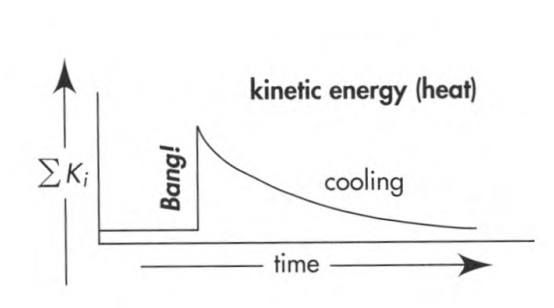
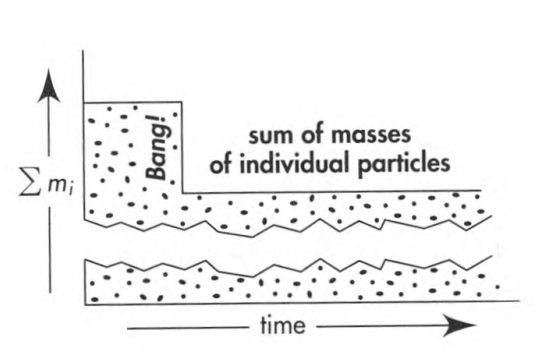
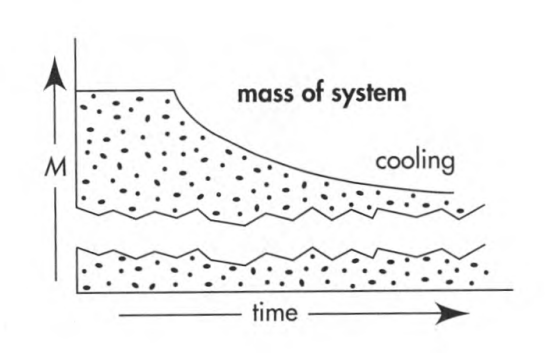
The mass of the products of a nuclear fission explosion (Section 8.7: fragments of split nuclei of uranium, for example) - contained in an underground cavity, allowed to cool, collected, and weighed - is this mass less than the mass of the original nuclear device?	Yes! The key point is the waiting period, which allows heat and radiation to flow away until transmuted materials have practically the same heat content as that of original bomb. In the expression for the mass of the system \[M_{\text {system }}=\sum_{i=1}^{n} m_{i}+\sum_{i=1}^{n} K_{i}\] [in zero-total mentum frame] the second term on the right, the kinetic energy of thermal agitation - whose value rose suddenly at the time of explosion but dropped during the cooling period - has undergone no net alteration as a consequence of the explosion followed by cooling. In contrast, the sum of masses \[\sum m_{i}\] has undergone a permanent decrease, and with it the mass \(M\) of what one weighs (after the cooling period) has dropped (see the figure)
Does Einstein’s statement that mass and energy are equivalent mean that energy is the same as mass?	No. Value of energy depends on the free-float frame of reference from which the particle (or isolated system of particles) is regarded. In contrast, value of mass is independent of inertial frame. Energy is only the time component of a momenergy 4-vector, whereas mass measures entire magnitude of that 4-vector. The time component gives the magnitude of the momenergy 4-vector only in the special case in which that 4-vector has no space component; that is, in a frame in which the momentum of the particle (or the total momentum of an isolated system of particles) equals zero. Only as measured in this special zero-momentum frame does energy have the same value as mass.
Then what is the meaning of Einstein’s statement that mass and energy are equivalent?	Einstein’s statement refers to the reference frame in which the particle is at rest, so that it has zero momentum \(p\) and zero kinetic energy \(K\). Then \(E=\) \(m+K \rightarrow m+0 .\) In that case the energy is called the rest energy of the particle: \[E_{\text {rest }}=m\] In this expression, recall, the energy is measured in units of mass, for example kilograms. Multiply by the conversion factor \(c^{2}\) to express energy in conventional units, for example joules (Table 7-1). The result is Einstein’s famous equation: \[E_{\text {rest, conv }}=m c^{2}\] Many treatments of relativity fail to use the subscript "rest" - needed to remind us that this equivalence of mass and energy refers only to the rest energy of the particle (for a system, the total energy in the zero-total-momentum frame).
Without delving into all fine points of legalistic phraseology, how significant is the conversion factor \(c^{2}\) in the equation \(E_{\text {rest, conv }}=m c^{2}\) ?	The conversion factor \(c^{2}\), like the factor of conversion from seconds to meters or miles to feet (Box 3-2), today counts as a detail of convention, rather than as a deep new principle.
If the factor \(c^{2}\) is not the central feature of the relationship between mass and energy, what is central?	The distinction between mass and energy is this: Mass is the magnitude of the momenergy 4-vector and energy is the time component of the same 4-vector. Any feature of any discussion that emphasizes this contrast is an aid to understanding. Any slurring of terminology that obscures this distinction is a potential source of error or confusion.
Is the mass of a moving object greater than the mass of the same object at rest?	No. It is the same whether the object is at rest or in motion; the same in all frames.
Really? Isn’t the mass, \(M\), of a system of freely moving particles given, not by the sum of the masses \(m_{i}\) of the individual constituents, but by the sum of energies \(E_{i}\) (but only in a frame in which total momentum of the system equals zero)? Then why not give \(E_{i}\) a new name and call it "relativistic mass" of the individual particle? Why not adopt the notation \(m_{i, \mathrm{rel}}=E_{i}=m_{i}+K_{i} ?\) With this notation, can’t one then write \(M=\sum_{i=1}^{n} m_{i, \mathrm{rel}} ?\) [in zero-total momentum frame]	Ouch! The concept of "relativistic mass" is subject to misunderstanding. That’s why we don’t use it. First, it applies the name mass - belonging to the magnitude of a 4-vector-to a very different concept, the time component of a 4-vector. Second, it makes increase of energy of an object with velocity or momentum appear to be connected with some change in internal structure of the object. In reality, the increase of energy with velocity originates not in the object but in the geometric properties of spacetime itself.
In order to make this point clear, should we invariant mass of a particle its "rest mass"?	That is what we called it in the first edition of this book. But a thoughtful student pointed out that the phrase "rest mass" is also subject to misunderstanding: What happens to the "rest mass" of a particle when the particle moves? In reality mass is mass is mass. Mass has the same value in all frames, is invariant, no matter how the particle moves. [Galileo: "In questions of science the authority of a thousand is not worth the humble reasoning of a single individual."’]
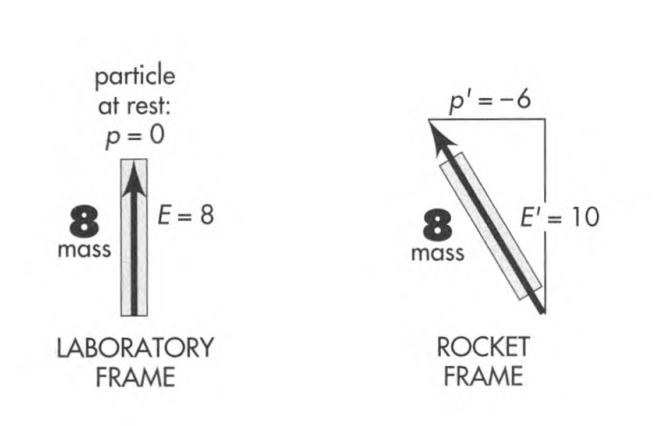
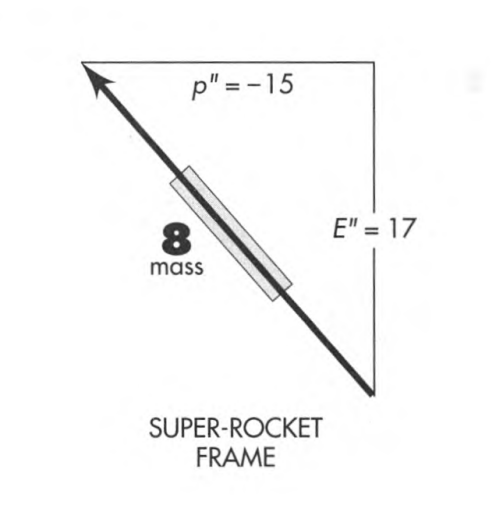
Can any simple diagram illustrate this contrast between mass and energy	Yes. The figure shows the momentum-energy vector of the same particle as measured in three different frames. Energy differs from frame to frame. Momentum differs from frame to frame. Mass (magnitude of 4-vector, represented by the length of handles on the arrows) has the same value, \(m=8\), in all frames.