11.7: Addition of Velocities

add light velocity to light velocity: get light velocity!

The Lorentz transformation permits us to answer decisively the apparent contradiction to special relativity outlined in Section 11.2, namely the apparent addition of velocities to yield a resultant velocity greater than that of light.

Return to velocity addition paradox

I travel in a rocket that you observe to move at \(4 / 5\) light speed. Out the front of my rocket I fire a bullet that I observe to fly forward at 4/5 light speed. Then you measure this bullet to streak forward at \(4 / 5+4 / 5=8 / 5=1.6\) light speed, which is greater than the speed of light. There!

Example \(\PageIndex{1}\) TRANSFORMING OVER AND BACK

A rocket moves with speed \(v_{\text {rel }}=0.866(\) so \(\gamma=2)\) along the \(x\)-direction in the laboratory. In the rocket frame an event occurs at coordinates \(x^{\prime}= 10 meters\), \(y^{\prime}=7\) meters, \(z^{\prime}=3\) meters, and \(t^{\prime}=\) 20 meters of light-travel time with respect to the reference event.

a. What are the coordinates of the event as observed in the laboratory?

b. Transform the laboratory coordinates back to the rocket frame to verify that the resulting coordinates are those given above.

Solution

a. We already know from Section 3.6 - as well as from the Lorentz transformation, equation 11.5.5 - that coordinates transverse to direction of relative motion are equal in laboratory and in rocket. Therefore we know immediately that

\[\begin{aligned} &y=y^{\prime}=7 \text { meters } \\ &z=z^{\prime}=3 \text { meters } \end{aligned} \nonumber \]

The \(x\) and \(t\) coordinates of the event as observed in the laboratory make use of the first two equations 11.5.5:

\[\begin{aligned} t &=v_{\text {rel }} \gamma x^{\prime}+\gamma t^{\prime}=(0.866)(2)(10 \text { meters })+(2)(20 \text { meters }) \\ &=17.32+40=57.32 \text { meters } \end{aligned} \nonumber \]

and

\[\begin{aligned} x &=\gamma x^{\prime}+v_{\text {rel }} \gamma t^{\prime}=2(10 \text { meters })+(0.866)(2)(20 \text { meters }) \\ &=20+34.64=54.64 \text { meters } \end{aligned} \nonumber \]

So the coordinates of the event in the laboratory are \(t=57.32\) meters, \(x=54.64\) meters, \(y=7\) meters, and \(z=3\) meters.

b. Use equation 11.6.1 to transform back from laboratory to rocket coordinates.

\[\begin{aligned} t^{\prime} &=-v_{\text {rel }} \gamma x+\gamma t=-(0.866)(2)(54.64 \text { meters })+(2)(57.32 \text { meters) }\\ &=-94.64+114.64=20.00 \text { meters } \end{aligned} \nonumber \]

and

\[\begin{aligned} x^{\prime} &=\gamma x-v_{\text {rel }} \gamma t=2(54.64 \text { meters })-(0.866)(2)(57.32 \text { meters }) \\ &=109.28-99.28=10.00 \text { meters } \end{aligned} \nonumber \]

as given in the original statement of the problem.

To analyze this experiment, convert statements about the bullet to statements about events, since event coordinates are what the Lorentz transformation transforms. Event 1 is the firing of the gun, event 2 the arrivaL of the bullet at the target. The Lorentz transformation equations can give locations \(x_{1}, t_{1}\) and \(x_{2}, t_{2}\) of these events in the laboratory frame from their known locations \(x_{1}^{\prime}, t_{1}^{\prime}\) and \(x_{2}^{\prime}, t_{2}^{\prime}\) in the rocket frame. In particular:

\[\begin{aligned} &x_{2}=\gamma x_{2}{ }^{\prime}+v_{\text {re }} \gamma t_{2}^{\prime} \\ &x_{1}=\gamma x_{1}{ }^{\prime}+v_{\text {re }} \gamma t_{1}{ }^{\prime} \end{aligned} \nonumber \]

Subtract corresponding sides of these two equations:

\[\left(x_{2}-x_{1}\right)=\gamma\left(x_{2}^{\prime}-x_{1}^{\prime}\right)+v_{\mathrm{rel}} \gamma\left(t_{2}^{\prime}-t_{1}^{\prime}\right) \nonumber \]

We are interested in the differences between the coordinates of the two emissions. Indicate these differences with the Greek uppercase delta, \(\Delta\), for example \(\Delta x\). Then this \(x\)-equation and the corresponding \(t\)-equation become

Incremental event separations define velocities

\[\begin{aligned} \Delta x &=\gamma \Delta x^{\prime}+v_{\text {rel }} \gamma \Delta t^{\prime} \\ \Delta t &=v_{\text {rel }} \gamma \Delta x^{\prime}+\gamma \Delta t^{\prime} \end{aligned}\]

The subscript "rel" distinguishes relative speed between laboratory and rocket frames from other speeds, such as particle speeds in one frame or the other.

Bullet speed in any frame is simply space separation between two events on its trajectory measured in that frame divided by time between them, observed in the same frame. In the special case chosen, only the \(x\)-coordinate needs to be considered, since the bullet moves along the direction of relative motion. Divide the two sides of the first equation \(\PageIndex{1}\) by the corresponding sides of the second equation to obtain laboratory speed:

\[\frac{\Delta x}{\Delta t}=\frac{\gamma \Delta x^{\prime}+v_{\text {rel }} \gamma \Delta t^{\prime}}{v_{\text {rel }} \gamma \Delta x^{\prime}+\gamma \Delta t^{\prime}}\]

Then the time stretch factor \(\gamma\) cancels from the numerator and denominator on the right. Divide every term in numerator and denominator on the right by \(\Delta t^{\prime}\).

\[\frac{\Delta x}{\Delta t}=\frac{\left(\Delta x^{\prime} / \Delta t^{\prime}\right)+v_{\mathrm{rel}}}{v_{\mathrm{re}}\left(\Delta x^{\prime} / \Delta t^{\prime}\right)+1}\]

Now, \(\Delta x^{\prime} / \Delta t^{\prime}\) is just distance covered per unit time by the particle as observed in the rocket, its speed - call it \(v^{\prime}\), with a prime. And \(\Delta x / \Delta t\) is particle speed in the laboratory - call it simply \(v\). Then (reversing order of terms in the denominator to give the result its usual form) the equation becomes

Law of Addition of Velocities

\[v=\frac{v^{\prime}+v_{\mathrm{rel}}}{1+v^{\prime} v_{\mathrm{rel}}}\]

This is called the Law of Addition of Velocities in one dimension. A better name is the Law of Combination of Velocities, since velocities do not "add" in the usual sense. Using the Law of Combination of Velocities, we can predict bullet speed in the laboratory. The bullet travels at \(v^{\prime}=4 / 5\) with respect to the rocket and the rocket moves at \(v_{\text {rel }}=4 / 5\) with respect to the laboratory. Therefore, speed \(v\) of the bullet relative to the laboratory comes from the expression

\[v=\frac{4 / 5+4 / 5}{1+(4 / 5)(4 / 5)}=\frac{8 / 5}{1+16 / 25}=\frac{8 / 5}{41 / 25}=\frac{40}{41} \nonumber \]

Thus the bullet moves in the laboratory at a speed less than light speed.

As a limiting case, suppose that the "bullet" shot out from the front of the rocket is, in fact, a pulse of light. Guess: What is the speed of this light pulse in the laboratory? Here is the calculated answer. Light moves with respect to the rocket at speed \(v^{\prime}=1\) while the recket continues along at a speed \(v_{\text {rel }}=4 / 5\) with respect to the laboratory. The light then moves with respect to the laboratory at speed \(v\) :

Light speed is invariant, as expected.

\[v=\frac{1+4 / 5}{1+(1)(4 / 5)}=\frac{9 / 5}{9 / 5}=1 \nonumber \]

So light moves with the same speed in both frames, as required by the Principle of Relativity. Question: Is this true also when a light pulse is shot out of the rear of the rocket?

Example \(\PageIndex{1}\) ET TU SPACETIME

Julius Caesar was murdered on March 15 in the year 44 в.с. at the age of 55 approximately 2000 years ago. Is there some way we can use the laws of relativity to save his life?

Let Caesar’s death be the reference event, labeled \(0: x_{0}=0, t_{0}=0\). Event \(A\) is you reading this exercise. In the Earth frame the coordinates of event \(A\) are \(x_{A}=0\) light-years, \(t_{A}=2000\) years. Simultaneous with event \(A\) in your frame, Starship Enterprise cruising in the Andromeda galaxy sets off a firecracker: event \(B\). The Enterprise moves along a straight line in space that connects it with Earth. Andromeda is 2 million light-years distant in our frame. Compared with this distance, you can neglect the orbit of Earth around Sun. Therefore, in our frame, event \(B\) has the coordinates \(x_{B}=2 X\) \(10^{6}\) light-years, \(t_{B}=2000\) years. Take Caesar’s murder to be the reference event for the Enterprise too \(\left(x_{0}^{\prime}=0, t_{0}^{\prime}=0\right)\).

a. How fast must the Enterprise be going in the Earth frame in order that Caesar’s murder is happening NOW (that is, \(t_{B}^{\prime}=0\) ) in the Enterprise rest frame? Under these circumstances is the Enterprise moving toward or away from Earth?

b. If you are acquainted with the spacetime diagram (Chapter 5), draw a spacetime diagram for the Earth frame that displays event \(O\) (Caesar’s death), event \(A\) (you reading this exercise), event \(B\) (firecracker exploding in Andromeda), your line of NOW simultaneity, the position of the Enterprise, the worldline of the Enterprise, and the Enterprise NOW line of simultaneity. The spacetime diagram need not be drawn to scale.

c. In the Enterprise frame, what are the \(x\) and \(t\) coordinates of the firecracker explosion?

d. Can the Enterprise firecracker explosion warn Caesar, thus changing the course of Earth history? Justify your answer.

Solution

a. From the statement of the problem,

\[\begin{aligned} x_{o} &=x_{o}^{\prime}=0 & x_{A} &=0 & x_{B} &=2 \times 10^{6} \text { light-years } \\ t_{o} &=t_{0}^{\prime}=0 & t_{A} &=2000 \text { years } & t_{B} &=2000 \text { years } \end{aligned} \nonumber \]

We want the speed \(v_{\text {rel }}\) of the Enterprise such that \(t_{B}^{\prime}=0 .\) The first two Lorentz transformation equations 11.5.5 with \(t_{B}^{\prime}=0\) become

\[\begin{aligned} t_{B} &=v_{\text {rel }} \gamma x_{B}{ }^{\prime} \\ x_{B} &=\gamma x_{B}{ }^{\prime} \end{aligned} \nonumber \]

We do not yet know the value of \(x_{B}{ }^{\prime}\). Solve for \(v_{\text {rel }}\) by dividing the two sides of the first equation by the respective sides of the second equation. The unknown \(x_{B}{ }^{\prime}\) drops out (along with \(\gamma\) ), and we are left with \(v_{\text {rel }}\) in terms of the known quantities \(t_{B}\) and \(x_{B}\) :

\[v_{\text {rel }}=\frac{t_{B}}{x_{B}}=\frac{2 \times 10^{3} \text { years }}{2 \times 10^{6} \text { years }}=10^{-3}=0.001 \nonumber \]

This is the desired speed \(v_{\text {rel }}\) between Earth and Enterprise frames. This velocity is a positive quantity, so the Enterprise moves in the positive \(x\)-direction, namely away from Earth.

Surprised to see a speed given as the ratio of a time separation to a space separation: \(t_{B} / x_{B}\) ? Then realize that \(x_{B}\) and \(t_{B}\) are not displacements of any particle. Nothing can travel the distance \(x_{B}\) in the time \(t_{B}\), as discussed in \(\mathrm{d}\). The goal here is to find a frame in which Caesar’s death and the firecracker explosion are simultaneous. For this limited purpose the rocket speed \(v_{\text {rel }}=t_{B} / x_{B}\) is correct.

Why is the relative velocity \(v_{\text {rel }}\) so small compared with the speed of light? Because of the large denominator \(x_{B}\) in the equation that leads to this value. Consider the string of Earth clocks stretching toward Andromeda when all Earth clocks read zero time (Caesar’s death). Enterprise clocks read (from equations 11.6.1 with \(t=0\) ) as follows: \(t^{\prime}=-v_{\text {re1 }} \gamma x\). This is an example of the relativity of simultaneity (Section 3-4). The farther the \(x\)-distance from Earth, the earlier will Enterprise clock read. With \(x=2\) million light-years, the relative speed \(v_{\text {rel }}\) does not have to be large to carry Enterprise time back 2000 years for Earth.

b.

Figure \(\PageIndex{1}\): Earth spacetime diagram, showing events \(0, A\), and \(B\). Not to scale.

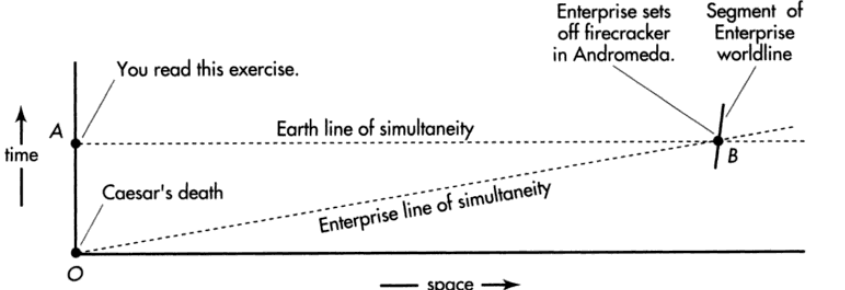
c. We need the value of gamma, \(\gamma\), for the inverse Lorentz transformation equation (11.6.1). This value is very close to unity, and from it come \(t_{B}^{\prime}\) and \(x_{B}^{\prime}\).

\[\begin{aligned} \gamma &=\frac{1}{\left[1-v_{\mathrm{rel}}^{2}\right]^{1 / 2}}=\frac{1}{\left[1-\left(10^{-3}\right)^{2}\right]^{1 / 2}}=\frac{1}{\left[1-10^{-6}\right]^{1 / 2}} \approx 1+\frac{10^{-6}}{2} \\ t_{B}{ }^{\prime} &=-v_{\mathrm{rel}} \gamma x_{B}+\gamma t_{B}=\gamma\left(-10^{-3} \times 2 \times 10^{6}+2 \times 10^{3}\right) \\ &=\gamma\left(-2 \times 10^{3}+2 \times 10^{3}\right)=0 \text { years } \\ x_{B}{ }^{\prime} &=\gamma x_{B}-v_{\mathrm{rel}} \gamma t_{B}=\gamma\left(2 \times 10^{6}-10^{-3} \times 2 \times 10^{3}\right)=2 \gamma\left(1-10^{-6}\right) 10^{6} \\ &=2\left(1+\frac{10^{-6}}{2}\right)\left(1-10^{-6}\right) 10^{6}=2\left(1-\frac{10^{-6}}{2}-\frac{10^{-12}}{2}\right) 10^{6} \\ & \approx 1.999999 \times 10^{6} \text { light-years. } \end{aligned} \nonumber \]

We chose the relative velocity so that the time of the firecracker explosion as observed in the rocket is the same as the time of Caesar’s death, namely \(t_{B}^{\prime}=0\). The \(x\)-coordinate of this explosion is not much different in the two frames because their relative velocity is so small.

d. There exists a frame - the rest frame of the Enterprise - in which Caesar’s death and the firecracker explosion occur at the same time. In this frame a signal connecting the two events would have to travel at infinite speed. But this is impossible. Therefore the Enterprise cannot warn Caesar; his death is final. Sorry. (Note: In the language of Chapter 6 , the relation between the two events is spacelike, and spacelike events cannot have a cause -effect relationship.) 108 SPECIAL TOPIC

WHY NOTHING TRAVELS FASTER THAN LIGHT

A material object traveling faster than light? No! If one did, we could violate the normal order of cause and effect in a million testable ways, totally contrary to all experience. Here we investigate one example, making use of Lorentz transformation equations.

The Peace Treaty of Shalimar was signed four years before the Great Betrayal. So pivotal an event was the Great Betrayal that it was taken as zero of space and time.

By the Treaty of Shalimar, the murderous Klingons agreed to stop attacking Federation outposts in return for access to the Federation Technical Database. Federation negotiators left immediately after signing the Shalimar Treaty in a ship moving at \(0.6\) light speed.

Figure \(\PageIndex{2}\): Klingon ("laboratory") spacetime diagram. The Klingon worldline is the vertical time axis. The Treaty of Shalimar is followed four years later by the Great Betrayal (event 0) at which Klingons launch the Super, which moves at three times light speed. Traveling from left to right, the Super passes one Federation colony (event 1) and then another (event 2). Finally the Super destroys the retreating ship of Federation negotiators (event 3 ).

Within four years the Klingons used the Federation Technical Database to develop a faster-than-light proiectile, the slaughtering Super. On that dark day of Great Betrayal (reference event 0), the Klingons launched the Super at three times light speed foward the retreating Federation ship.

Two Federation space colonies lay between the Klingons and the point of impact of the Super with the Federation ship. A lonely lookout at the first colony witnessed with awe the blinding passage of the Super levent 1). Later many citizens of the second colony gaped as the Super demolished one of their communication structures (event 2) and zoomed on. Both colonies desperately sent warnings toward the Federation ship, but to no avail since the Super outran the radio signals.

Finally, at event 3, the Super overtook and destroyed the Federation ship. All Federation negotiators were lost in a terrible flash of light and scattering of debris. A long dark period of renewed warfare began.

But wait! Look again at events of the Great Betrayal, this time from the point of view of the Federation rocket ship. Where and when does the Great Betrayal occur in this frame? The Great Betrayal is the "hinge of history," the reference event, the zero of space and time coordinates for all laboratory and rocket frames.

Where and when does the Super explode (event 3) in this rocket frame? In the Klingon "laboratory" frame, event 3 has coordinates \(x_{3}=3\) light-years and \(t_{3}=1\) year. Use the inverse Lorentz transformation equations to find the location of event 3 in the rocket frame of the Federation negotiators. Calculate the time stretch factor \(\gamma\) using speed of the Federation rocket, \(v_{\text {rel }}=0.6\), with respect to the Klingon frame:

\[\begin{aligned} \gamma &=\frac{1}{\left[1-v_{\mathrm{rel}}^{2}\right]^{1 / 2}}=\frac{1}{\left[1-(0.6)^{2}\right]^{1 / 2}}=\frac{1}{[1-0.36]^{1 / 2}} \\ &=\frac{1}{[0.64]^{1 / 2}}=\frac{1}{0.8}=1.25 \end{aligned} \nonumber \]

Figure \(\PageIndex{3}\): "Rocket" spacetime diagram of departing Federation negotiators. In this frame their destruction comes first (event 3), followed by the passage of the Super from right to left past Federation colonies in reverse order (event 2 followed by event 1). Finally, the Super enters the Klingon launcher without doing further damage (event 0). The Great Betrayal bas become the Great Confusion of Cause and Effect.

Substitute these values into equations 11.6.1 to reckon the rocket coordinates of event 3 :

\[\begin{aligned} t_{3}^{\prime} &=-v_{\text {rel }} \gamma x_{3}+\gamma t_{3} \\ &=-(0.6)(1.25)(3 \text { years })+(1.25)(1 \text { year }) \\ &=-2.25 \text { years }+1.25 \text { years }=-1 \text { year } \\ x_{3}^{\prime} &=\gamma x_{3}-v_{\text {rel }} \gamma t_{3} \\ &=(1.25)(3 \text { years })-(0.6)(1.25)(1 \text { year }) \\ &=3.75 \text { years }-0.75 \text { year }=3 \text { years } \end{aligned} \nonumber\]

Event 3 is plotted in the rocket diagram and the worldline of the Super drawn by connecting event 3 with the launching of the Super at event 0 . Notice that this worldline slopes downward to the right. More about the significance of this in a minute.

In a similar manner find the rocket coordinates of the treaty signing at Shalimar (subscript Sh), which has laboratory coordinates \(x_{\mathrm{Sh}}=0\) and \(t_{\mathrm{Sh}}=-4\) years:

\[\begin{aligned} t_{\mathrm{Sh}}^{\prime} &=-v_{\mathrm{rel} 1} \gamma \mathrm{x}_{\mathrm{Sh}}+\gamma t_{\mathrm{Sh}} \\ &=-(0.6)(1.25)(0 \text { years })+(1.25)(-4 \text { years }) \\ &=-5 \text { years } \\ x_{\mathrm{Sh}}^{\prime} &=\gamma x_{\mathrm{Sh}}-v_{\mathrm{rel}} \gamma t_{\mathrm{Sh}} \\ &=(1.25)(0 \text { years })-(0.6)(1.25)(-4 \text { years) }\\ &=+3 \text { years } \end{aligned} \nonumber \]

In the Federation (rocket) spacetime diagram, the worldline of Federation negotiators extends from treaty signing at Shalimar vertically to explosion of the Super (event 3). The worldline of the Klingons extends from Shalimar diagonally through the launch of the Super at event 0

In the Federation spacetime diagram, the worldline for the Super tilts downward to the right. In this frame deaths of Federation negotiators (event 3) occur at a time \(t_{3}^{\prime}=\) minus 1 year, that is, before the treacherous Klingons launch the Super at the event of Great Betrayal (reference event 0). From the diagram one would say that the Super moves with three times light speed from Federation ship toward the Klingons. This seems to be verified by the fact that in this frame the Super passes Federation colonies in reverse order, event 2 followed by event 1 , going in the opposite direction. Yet Federation negotiators have created no such terrible weapon and in fact are destroyed by it at the moment they are supposed to launch it, as proved by the flying photons and debris. More: Klingons suffer no damage from the mighty impact of the slaughtering Super (event 0). Rather, in this frame it enters their launching cannon mild as a lamb.

What have we here? A confusion of cause and effect, a confusion that cannot be straightened out as long as we assume that the Super - or any other material object - travels faster than light in a vacuum.Why does no signal and no object travel faster than light in a vacuum? Because if either signal or object did so, the entire network of cause and effect would be destroyed, and science as we know it would not be possible

Example \(\PageIndex{3}\) THE FIRING MESON

A \(K^{\circ}\) (pronounced " \(K\)-naught") meson at rest in a rocket frame decays into \(\pi^{+}\)("pi plus") meson and a \(\pi^{-}\)("pi minus") meson, each having a speed of \(v^{\prime}=0.85\) with respect to the rocket. Now consider this decay as observed in a laboratory with respect to which the \(K^{\circ}\) meson travels at a speed of \(v_{\text {rel }}=0.9\). What is the greatest speed that one of the \(\pi\) mesons can have with respect to the laboratory? What is the least speed?

Solution

Let the speeding \(K^{\circ}\)-meson move in the positive \(x\)-direction in the laboratory. In the rocket frame, daughter \(\pi\)-mesons come off in opposite directions. Their common line of motion can, however, be oriented arbitrarily in this frame. The maximum speed of a daughter \(\pi\)-meson in the laboratory results when it is emitted in the forward \(x\)-direction. For such a meson, the law of addition of velocities gives

\[v_{\max }=\frac{v^{\prime}+v_{\mathrm{rel}}}{1+v^{\prime} v_{\mathrm{rel}}}=\frac{0.85+0.9}{1+(0.85)(0.9)}=\frac{1.75}{1.765}=0.9915 \nonumber \]

Thus adding a speed of \(0.85\) to a speed of \(0.9\) does not yield a resulting speed greater than 1, light speed.

The slowest laboratory speed for a daughter meson occurs when it is emitted in the negative \(x\)-direction in the rocket frame. In this case the velocity of the daughter meson is negative and the law of addition of velocities becomes a law of subtraction of velocities:

\[v_{\min }=\frac{-v^{\prime}+v_{\mathrm{rel}}}{1-v^{\prime} v_{\mathrm{rel}}}=\frac{-0.85+0.9}{1-(0.85)(0.9)}=\frac{0.05}{0.235}=0.2128 \nonumber \]

Although the minimum-speed meson moves to the left in the rocket, it moves to the right in the laboratory because of the very great speed of the original \(K^{\circ}-m e s o n\) in the laboratory.