SPECIAL RELATIVITY

Introduction.

The Principle of Relativity states that:

The laws of mechanics are the same in all inertial reference frames

or, in different words,

All inertial frames are equivalent; there is no preferred inertial frame ...

(An early form of this principle was first enunciated by Galileo in "The Dialogue on the Great World Systems". )

What's an Inertial Reference Frame? One in which the Law of Inertia holds (circular definition??).

Meaning that ----A non-spinning frame, isolated in deep space, with no local sources of gravitation or other forces is an inertial frame. All other frames of reference which are moving uniformly (i.e. with constant velocity) with respect to this one are inertial frames. Any frame that is accelerating in any way with respect to such inertial frames, is not an inertial frame.

All inertial frames are equivalent ---- means that there is no way to determine which frame is "moving" or which is "at rest". Which, in turn, implies that the laws of physics are the same for observers in all inertial frames.

Where can I find an Inertial Frame? Rather surprisingly, in spite of the fact that we are more or less fixed on the surface of a spinning planet, which is orbiting a star which is itself orbiting the center of our galaxy, which itself is moving through the universe, frames fixed in our earth-bound laboratories are good approximations to inertial frames.

What does it all mean? Of course observers in different frames would see different things if they were both observing the same phenomena - e.g. the speed of the ball in one frame would be different from the speed of the ball measured by an observer in another frame. The Principle of Relativity says only that if observers in different frames perform the same experiment, they must arrive at identical conclusions. Newton's Laws would be the same in all inertial frames, a game of billiards played on a uniformly moving train would obey the same laws as one in the local pool hall, table tennis played on a smoothly moving ship would be obey the same rules as that in the local gymnasium, etc.

Technical Note: The Principle of Relativity seems unexceptional for the laws of mechanics, since it corresponds to our everyday experience. In fact it was assumed to be true by all classical physicists for all mechanical phenomena. However it is more problematical for electromagnetism. We might expect that two observers in different frames would still get identical results if they did the same experiment; e.g. the same amount of current would flow in a wire subject to the same voltage, the forces between two charged objects would still obey Coulomb's Law etc. - and indeed the Principle of Relativity does hold for these phenomena. Thus two observers in two different uniformly moving frames would be expected to find that Maxwell's equations, in exactly the same form, would hold in their own frames - and indeed they do.

BUT, the astonishing thing about Maxwell's equations is that they predict the speed of electromagnetic radiation (the speed of light, c) to be a product of two constants of nature (remember c=1/ (square root of product of two universal constants?) which depend not at all on the relative speed between observers. So Maxwell's theory tells that all observers would measure the same value of c, whereas classical mechanics would insist that the measurement of a speed of any object must take into account the motion of the observer. This discrepancy between mechanics and electromagnetism led Einstein to enunciate two postulates on which the theory of Special Relativity rests.

We can restate Einstein's postulates as follows:

I Einstein's Postulate I : All inertial frames are completely equivalent for all physical phenomena.

I I Einstein's Postulate II : The speed of light is the same in all inertial reference frames.

ALL THE RESULTS OF THE SPECIAL THEORY OF RELATIVITY FOLLOW FROM THESE TWO POSTULATES

We will now follow through on the consequences of these two hypotheses by a series of examples which will lead us very far from the views of classical physics.

Example 1:

Some Lengths are Invariant. We can use Postulate I to prove that a meter stick moving with a constant speed perpendicular to its length will have the same length as a stationary one. (Of course, Newtonian physics would take this statement to be self-evident; however, in the world of Special Relativity we cannot make such assumptions). Suppose both sticks are upright, one each held by observers Jack and Jill. Suppose Jack hypothesizes that the length of meter sticks moving perpendicular to their lengths decrease; let us then attach a paint brush to the top end of Jill's stick. Then let Jill, holding her stick, move past Jack at a constant speed. The brush on Jill's stick will make a mark on Jack's stick, at some point below the top end of his stick (since, by hypothesis, moving sticks shrink); the existence of this mark can be confirmed by both Jack and Jill. However, from Jill's point of view, it is Jack who is moving; the appearance of the mark on Jack's stick indicates that his stick has grown. Thus both Jack and Jill have performed an identical experiment - the observation of a moving stick, and have not reached the same result, as the Principle of Relativity says they must. (Alternatively you could say that they disagree on a "law" of physics which states that sticks moving perpendicular to their lengths shrink: the Principle of Relativity doesn't allow this sort of disagreement). The only solution is that Jack's hypothesis is wrong.

[You might like to check that you understand this argument by repeating it for yourself, but with the hypothesis that a meter stick moving with a constant speed perpendicular to its length will increase in length; then you might compare this argument with the one we develop later for a meter stick moving parallel to its length.]

Example 2:

Time Dilation. A clock is just a device which gives a periodic signal (a "tick"!) to note the passage of time. Suppose that we have a clock which we will call a Light Clock. It consists of a flashing light bulb a distance w from a mirror; when a flash of light from the bulb reflects back from the mirror it triggers the next flash of light. Thus the "tick"(the basic time unit) of this clock is given by the time taken for the light to leave the bulb, bounce off the mirror, and return to the bulb (see Figure I). Now suppose that Jack and Jill each have identical Light Clocks. Suppose that Jill is sitting with her Light Clock on a train that is speeding towards a station, on whose platform Jack is sitting (Jack and Jill are thus in relatively moving Inertial frames of reference).

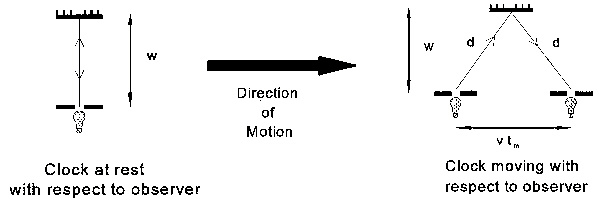
Figure I Figure II

If the clocks are oriented so that the direction of the light is perpendicular to that of the train's motion, Jack's view of Jill's clock will be that of Figure II. It is clear from this figure that Jack will observe that the light in Jill's clock takes longer to complete its trip to the mirror and back again than does the light in his clock, since, in his frame of reference, it has further to go. Since the speed of the light he measures is not affected by the movement of Jill's clock (by Einstein's second postulate), he must conclude that the "ticks" of Jill's clock, moving with respect to him, will be longer than the ticks of his (identical) clock. Of course the system is symmetric, since Jill could consider herself at rest, and Jack rushing towards her. Thus we conclude that moving clocks run slow.

Question: Does this Happen with ALL clocks? We might argue that these are rather strange clocks, and this odd effect, called Time Dilation is merely an artifact of their strange construction. However, suppose that Jill has another clock, of a quite different construction - for the sake of discussion, let's suppose she owns a modern quartz crystal watch. Let her calibrate this watch with respect to her Light Clock, when both are at rest in her frame of reference. Then she knows exactly how many ticks of the Light Clock correspond to a second on her watch. As time goes by, the clock and the watch will remain exactly in step, as long as they remain at rest in her frame of reference. However Jack certainly sees the Light Clock running slow. Since both Jack's and Jill's observations must be believed - why would they lie?? - the only way we can avoid a contradiction is by accepting that Jill's watch, as viewed by Jack, slows down by exactly the same amount as her Light Clock.

If this doesn't entirely convince you, consider the following argument. Give Jack an identical quartz watch, and suppose that quartz watches don't exhibit this strange relativistic effect, but keep exactly the same time in all inertial frames. Then Jack's watch and Light Clock will of course keep the same time, whereas Jill's clocks will tick at different rates (according now to both Jack and Jill). Thus we have a way of defining a special inertial frame - one in which the quartz clock and the Light Clock keep the same time - in contradiction to the Principle of Relativity. Or, we could say, equivalently, that Jack and Jill have performed the same experiment - observation of the Light Clock and the quartz watch - and have come up with a different result. Again, not allowed by Einstein's second postulate. Thus all clocks, including biological ones, exhibit time dilation. The above arguments could be restated thus: if Jill observes that she ages at a different rate from her clocks, she would have to agree that she was in motion relative to another observer who aged at the same rate as his clocks.

For those of you who want to see the mathematics of time dilation, consider Jack's view of things when Jill approaches him at a speed v (see Figure II). Let the unit of time measured on his Light Clock (at rest with respect to him) be t₀ ; let the unit of time measured by him on Jill's Light Clock (moving with respect to him at a speed v) be t_m . Then t₀ = 2w/c and t_m = 2d/c where c is the speed of light and d is shown in Figure II. In the time the light takes to make its round trip from the bulb to the mirror and back again, the moving clock has moved forward a distance v t_m. By Pythagoras' Theorem, d² = w² + (v t_m/2)². If we substitute for d and w in this expression, we obtain (ct_m)² = (ct₀)² + (v t_m)². Rearranging yields t_m = gt₀ , where g = (1-(v/c)²)^-1/2 .

Example 3:

The Relativity of Simultaneity. Consider the following situation. Jill is sitting at the center of a train which is moving relative to Jack, who waits on the station platform. Thus both are in relatively moving Inertial frames of reference. Suppose that there are two clocks situated one at each end of the train, exactly equidistant from Jill; let us call them the Front Clock and the Back Clock. Both are identical, and can be started by hitting them with a pulse of light.

At some time before she reaches Jack, Jill sends out a light pulse. Since she is equidistant from each clock and since the speed of light is the same in all directions, the clocks will be hit, and thus started, at exactly the same time in Jill's frame of reference. For Jill, then, the clocks are exactly synchronized. For Jack, however, the situation is different. He also knows that the speed of light is the same whether the pulse is speeding towards the Front Clock or the Back Clock. However, in his frame, the Back Clock is moving up to meet the pulse of light, which thus has to go a shorter distance before it hits (and starts) the Back Clock; similarly, since the Front Clock is moving away from the origin of the pulse of light, it will be hit (and started) at a later time. Thus, from Jack's point of view, the clocks have not been started simultaneously; in fact, according to him, the Front Clock is set slow compared to the Back Clock, since it was started later.

Question: Suppose Jill organized another method of synchronizing her clocks. For example, suppose she has a new pair of clocks (for convenience let's call the original ones Set A, and the new ones Set B). The Set B clocks are different from the Set A clocks but identical to each other; they don't need a light beam to start them, but can be started by pushing on a button on the top of the clock. Suppose now that Jill has long but exactly equal length arms, and that she sits sideways on the train with her arms stretched out, with one Set B clock in each hand. At a given moment, she pushes the button on each clock; surely now Jack must agree that the clocks have been synchronized?

It turns out that we do not need to get into the mechanism whereby the nerve impulses leave Jill's brain and travel along her arms to activate her fingers. There is a general argument which proves that any method of synchronizing two clocks will lead to disagreement between Jack and Jill.

Suppose Jill sets up both sets of clocks as before, and arranges to start all four clocks in Set A and Set B at exactly the same time (in her frame, of course). Then she will observe that the Set A clocks are exactly synchronized with the Set B clocks. In particular both Front Clocks (one from each set) will read the same time, and both Back Clocks will read the same time. But Jack observes that the Set A Front Clock is set slow compared to the Set A Back Clock. Now Jill's belief is undeniable; as indeed, by our earlier argument, is Jack's. Thus the only way these two (correct) views of the situation can be reconciled is if the Set B clocks behave in exactly the same way as the Set A clocks.

Question: But suppose that Jill synchronizes Set B clocks by starting them both at the center of the train where she sits; she then walks along the train and puts one clock at the Front, and then walks back to place the other clock at the Back. Surely Jack must agree that she has synchronized the clocks correctly this time?

Of course we know that moving clocks run slow, so we might expect that each clock loses a little time during its passage from the middle of the train to each end. However, Jill can certainly time her walk to the Back and Front so that both clocks were moved to their final positions at exactly the same speed, so that their rate of slowing and thus their synchronization remains identical. For Jack, on the other hand, the situation of both clocks is far from symmetric. The clock that was moved to the Front had a greater speed relative to him than the one that was moved to the Back; the Front clock thus lost more time and now reads behind the Back clock.

Note. Both clocks, initially at rest at the center of the train, do experience some acceleration and deceleration when they are moved; however we can, in principle, make this effect arbitrary small, and thus exclude such non-Special Relativistic effects from consideration.

Of course we could also have used the argument developed in the previous Question to arrive at the same result. In fact it is clear that this argument can be applied to any sort of clock, and any sort of synchronizing mechanism. Jack will always find that Jills' Front Clock is set behind her Back Clock. The judgment of simultaneity is relative - it depends on the observer's reference frame.

Example 4:

Length Contraction. Now suppose that Jack and Jill measure the length of Jill's train. For Jill, of course, it is easy; she can just pace it out, since it is at rest with respect to her. However Jack has a more difficult task, since he has to measure the position of both ends at the same time in his frame of reference. Jill offers to help him by stationing a friend at the Front of the train, and another at the Back of the train. At the moment she, sitting at the center of the train, is directly opposite Jack, she will emit a pulse of light; this will be the signal for her friends to drop markers on the station. Since both friends are exactly equidistant from Jill, they will drop their markers at exactly the same time (in Jill's frame). Jill now tells Jack that the distance between the markers is the length of the rod. Jack, however, objects to this arrangement. He notes that, in his frame of reference, Jill's friend at the Back of the train received the light signal before the friend at the Front; according to him, the back marker was dropped first, then, after the train had moved on a little, the second marker was dropped. Thus he informs Jill that the markers are too far apart to indicate the correct length. According to him, Jill's measurement of lengths stationary with respect to her is too great, which means that his measurement of a length which is moving with respect to him would yield a value less than that of Jill. Moving lengths contract. See Figure III for a diagram of Jack's view of things.

Figure III

For those of you who would like to see the mathematics of length contraction, one (deceptively)easy way is the following. Let the relative speed of Jack and Jill be v. Suppose they are both measuring a rod which is fixed in Jack's frame with its length parallel to the direction of relative motion; suppose that the length of the rod in Jack's rest frame is L₀. We are interested in Jill's measurement of this rod, which, in her frame, is moving with a speed v. Suppose Jack chooses the (odd!) method of measuring this length by measuring the time that Jill, traveling at a speed v, takes to move from the beginning of the rod to the end; i.e. he measures the time between "Event 1" (Jill is opposite one end of the rod) and "Event 2" (Jill is opposite the other end of the rod). Let this time be t₀, so that Jack's measurement of the length is L₀ = vt₀. Now let Jill measure the length of the rod by observing the time the rod takes to pass her; she thus measures the time between the same two events as Jack. However, since Jack sees her moving, he will claim that her clock is running slow and that her measurement of the time between the two events must be less than his by the factor g (remember, g is always greater than 1). Thus Jack finds that her measurement of the time the rod takes to pass her is t₀ /g and her measurement of the length of the rod must be L m = v t₀/g = L₀ /g . The length of the rod, moving in the direction of its length, is less than its length when stationary.

Example 5:

Distortion of High Speed Objects. How would objects moving past us at very high speeds look? Again suppose that Jill is sitting at the center of a train which is rushing towards Jack, who is standing at rest on the platform of the next station. Consider Jack's view of the train just at the moment when Jack and Jill are opposite each other, Jill at the center of the train, Jack on the platform; call this moment "now". What will Jack see?

Suppose it is daytime so that it is the Sun's reflected light from the train that enables Jack to see it. The light coming from the center of the train will reach him (almost) immediately, since he is directly opposite it. However the light coming from the back of the train which reaches him at the same time, has had to come from a much longer distance, and therefore had to set out much earlier, when the back of the train was further away than it is now. Jack's eyes, since they have had no experience with such events, will not make the correction, but will treat the current view of the centre and the earlier view of the back of the train as if they were both current. Since he is seeing the back of the train when it was much further away, the back half of the train will appear to him to be greatly stretched out.

Using similar arguments, a little thought will convince you that the front half of the train will appear to Jack to be compressed. Note that this is a different question from that concerning the length of the train that Jack would actually measure. Although his eyes may be not capable of making the required corrections for the time the light reaches him, his brain is able to do the necessary calculations (let's assume that he is an PHY100F graduate!) Jack's measurement of the entire length of the train will always yield a value which is less than the length that Jill measures, since the overall effect must be that of length contraction in the direction of motion; of course dimensions at right angles to the direction of motion will look the same to both observers (see Example 1).

Example 6:

The Twin Paradox. One of the most famous "paradoxes" of Special Relativity concerns the fate of a pair of twins; suppose they are again the ubiquitous Jack and Jill. One day Jill leaves earth and moves off at a very high speed to visit a distant planet. During her trip, her clocks (including her biological one) run more slowly than those of earth-bound Jack, and when she returns she will find that poor old Jack has aged much more than she has.

But wait a minute: from Jill's point of view, it is Jack who has moved off, away from her. It is thus his clocks that run slowly compared to hers; when they meet again it will be she who has aged much more than her traveling twin! Obviously, this is nonsense, but wherein lies the difficulty?

The resolution of this "paradox" comes about when we realize that the situation is not symmetric. Jack remains in one inertial frame throughout the period whereas Jill must change inertial frames at the half-way point. She starts off by moving away from Jack, but finishes her journey rushing towards him, and it is in this change of frames that the dominating effect lies. (It is not simply that the aging effect is caused by her acceleration and deceleration. This is because, at least in principle, we can make the time of her acceleration at the start of her journey as she moves from rest, at the halfway point when she turns around and at the end as she slows down (negative acceleration) as small a fraction of her entire journey as we choose.)

Let us look at a specific example.

Suppose that Jill sets off one day to a distant space station, call it Dravidia, which is 25 light years from Earth (i.e. measured in the system in which Earth and Dravidia are at rest). A light year is a measure of distance equal to the distance light can travel in a year.

Suppose that she speeds up almost immediately to a speed of 99.98% of the speed of light; this means that her Lorentz factor is close to 50. In order to discuss what happens let us imagine instead that she starts her trip jumping instantaneously on to a spaceship (call it Enterprise) which is speeding past Earth with 99.98% of the speed of light, headed directly for Dravidia. At Dravidia, she instantaneously jumps on to Enterprise's sister ship, Voyager, which is speeding towards Earth with 99.98% of the speed of light, and just happens to be at Dravidia at exactly the time Jill and the Enterprise reach there. So from her point of view, the Earth-Dravidia distance is length-contracted to be only 25/50 = half a light year. Since she is traveling at very close to the speed of light, it takes her just over 6 months by her clock to reach Dravidia, and 6 more to return. Thus, Jill's biological clock will have advanced by only one year.

Stay-at-home Jack sees things slightly differently. For him, Jill's clocks are running slow by a factor of 50. From his vantage point, she has to cover 50 light years for the return journey, which, at 99.98% of the speed of light, will take her just a fraction over 50 years as measured on Jack's clock. However, according to Jack, Jill's time-keeping is slow by a factor of 50, so he will agree that her clocks will only read 50/50 = one year, and that therefore she has aged by only one year compared to his fifty. So far, both Jack and Jill agree.

However, the apparent paradox arises when we consider what view Jill has of Jack's aging process. She sees Jack moving away from her at 99.98% of the speed of light. Thus, from her point of view, it is Jack's clocks that are running slow by a factor of 50. In her one year of travel, she will surely estimate that only 1/50 years have passed on Earth. So apparently she expects that Jack will have aged by just over one week, while she has aged by one year. Wherein lies the discrepancy?

The answer lies in the setting of clocks as viewed by a moving frame. Suppose that two clocks are set up, one on Earth and one on Dravidia, and that they are synchronised to read the same time on both Earth and Dravidia. However they will not be so synchronized as viewed from the Enterprise or from the Voyager. Remember that in Example 3 above the "Back" clock is seen to be set ahead of the "Front" clock from the point of view of an observer moving with respect to both clocks. In the present case, as viewed by the Enterprise, the "Back" clock is that on Dravidia. Suppose Jill sets her clock to agree with Jack's Earth-bound clock. Then, with a Lorentz factor of 50, it can be shown that the clock on Dravidia, as viewed by Jill at the start of her outgoing trip aboard the Enterprise, will appear to her to be set very nearly 25 years ahead of the one on Earth. When she reaches Dravidia, she will find that the Dravidia clock reads just over 25 years ahead of her clock.

A similar effect occurs on her return journey. When she jumps on to the Voyager, the "Back" clock is now the one on Earth, which is thus, according to Jill, set ahead of her clock (and the one on Dravidia) by almost 25 years. Thus when she finally returns to Earth she will find that the Earth clock reads very slightly over 50 years ahead of hers. Indeed she will agree that Jack has aged by about 50 years during her trip.

In fact, this effect has been measured by taking an atomic clock round the world on commercial airlines. The traveling clock indeed lost time, exactly as predicted by Special Relativity. We must conclude that indeed, travel keeps you young!

Example 7:

The Shrinking Garage. Another subtle "paradox" is the following. Jill races at high speed towards her garage, which is exactly the same length as her car when it is parked inside. Jack, standing inside the garage, measures the length of the speeding car to be less than that of the garage, so he will believe that the car can totally fit into the garage for a brief instant. However from Jill's point of view, it is the garage which shrinks, so she will find that the garage is too small to contain all of her car for even a brief instant. This time the resolution of the paradox arises from an extension of the results of Example 4. There we saw that two events which are simultaneous in one frame need not be so in another frame which is moving relative to it. Similarly, if the time between two events is extremely close in one frame their order may even be reversed in the other.

Example 8:

The Relativistic Mass Increase. These notes would not be complete without at least a mention of the most famous of all equations which arise out of Special Relativity -- E = mc². It is difficult without at least a little algebra to fully demonstrate what this equation means. However, the following brief discussion might convince you of its plausibility, and intrigue you enough to read more widely. One of the most sacred principles of Physics is that of Momentum Conservation. In the present context this means that the sum of momenta of two particles is the same before and after a collision between them. Now momentum is just the product of mass and velocity, and velocity is the quotient of distance and time. Since both distance and time have different values when measured from different frames of reference, it is perhaps not too surprising that velocity demonstrates a relativistic effect. But if the value of velocity depends on the frame in which it is measured, so must the value of mass, so that the product of mass and velocity has the same value in any frame. In fact the mass of a moving object can be shown to be greater than the mass of the same object when measured at rest.

But what can this mean? It turns out that the relativistic change in mass is due to the fact that mass and energy turn out to be exactly the same physical quantity. The definition of mass must therefore include all forms of energy associated with the object. Mass and energy turn out to be completely equivalent. However, the units used in their original definitions are quite different, so to convert from one to the other, a conversion factor is necessary; it turns out to be just the square of the speed of light, c². The rest mass of an object is the mass we measure when the object is at rest in our frame of reference. This is the mass that we are accustomed to use in our "normal", non-relativistic environment.