Special Theory of Relativity

INTRODUCTION

In this document we discuss Einstein's Special Theory of Relativity. The treatment is non-mathematical, except for a brief use of Pythagoras' theorem about right triangles. We concentrate on the implications of the theory. The document is based on a discussion of the the theory for an upper-year liberal arts course in Physics without mathematics; in the context of that course the material here takes about 4 or 5 one-hour classes.

Einstein published this theory in 1905. The word special here means that we restrict ourselves to observers in uniform relative motion. This is as opposed the his General Theory of Relativity of 1916; this theory considers observers in any state of uniform motion including relative acceleration. It turns out that the general theory is also a theory of gravitation.

Sometimes one hears that the Special Theory of Relativity says that all motion is relative. This is not quite true. Galileo and Newton had a similar conception. Crucial to Newton's thinking is that there is an absolute space, independent of the things in that space:

"Absolute space, in its own nature, without relation to anything external, remains always similar and immovable. Relative space is some movable dimension or measure of the absolute spaces; which our senses determine by its position to bodies .. because the parts of space cannot be seen, or distinguished from one another by our senses, there in their stead we use sensible [i.e. perceptible by the sense] measures of them ... but in philosophical disquisition, we ought to abstract from our senses, and consider things themselves, distinct from what are only sensible measures of them." -- Principia I, Motte trans.

For Newton, the laws of physics, such as the principle of inertia, are true in any frame of reference either at rest relative to absolute space or in uniform motion in a straight line relative to absolute space. Such reference frames are called inertial. Notice there is a bit of a circular argument here: the laws of physics are true in inertial frames, and inertial frames are ones in which the laws of physics are true.

In any case, from the standpoint of any such inertial frame of reference all motion can be described as being relative. If you are standing by the highway watching a bus go by you at 100 km/hr, then relative to somebody on the bus you are traveling in the opposite direction at 100 km/hr.

This principle, called Galilean relativity, is kept in Einstein's Theory of Relativity.

Many of the consequences of the Special Theory of Relativity are counter-intuitive and violate common sense. Einstein correctly defined common sense as those prejudices that we acquire at an early age.

THE CONSTANCY OF THE SPEED OF LIGHT

Once we realize that light is some sort of a wave, a natural question is "what is waving?" One answer to this question is that it is the luminiferous ether. The idea behind this word is that there is an all-pervading homogenous massless substance everywhere in the universe, and it is this ether that is the medium through which light propagates. Note that this ether could define Newton's absolute space.

A rough analogy is to a sound wave traveling through the air. The air is the medium and oscillations of the molecules of the air are what is "waving." The speed of sound is about 1193 km/hr with respect to the air, depending on the temperature and pressure. Thus if I am traveling through the air at 1193 km/hr in the same direction as a sound wave, the speed of the wave relative to me will be zero.

The speed of light is measured to be about 1,079,253,000 km/hr, and presumably this is its speed relative to the ether. Presumably the ether is stationary with respect to the fixed stars. This section investigates these two presumptions.

Galileo attempted to measure the speed of light around 1600. He and a colleague each had a lantern with a shutter, and they went up on neighboring mountains. Galileo opened the shutter on his lantern and when his colleague saw the light from Galileo's lantern he opened the shutter on this lantern. The time delay between when Galileo opened the shutter on his lantern and when he saw the answering light from his colleague's lantern would allow him to calculate the speed of light. This is absolutely correct experimental procedure in principle. However, because of our human reaction times the lag between when the colleague saw the light from Galileo's lantern until when he could get the shutter of his lantern open is so long that the light could have circled the globe many many times.

In 1676 Römer successfully measured the speed of light, although his results differed from the accepted value today by about 30%

The Michelson-Morley Experiment

In this sub-section we discuss a famous experiment done in the late nineteenth century by Michelson and Morley. Some knowledge of the fact that light is a wave and can undergo interference is assumed. A discussion of this occurs in the the first two sections of the document http://www.upscale.utoronto.ca/GeneralInterest/Harrison/DoubleSlit/DoubleSlit.html.

In is ironic that Michelson himself wrote in 1899, "The more important fundamental laws and facts of physical reality have all been discovered and they are now so firmly established that the possibility of their ever being supplanted in consequence of new discoveries is exceedingly remote .... Our future discoveries must be looked for in the 6th place of decimals." At this time there were a couple of small clouds on the horizon. One of those clouds was his own experiment with Morley that we describe in this sub-section. As we shall see, the experiment played a part in the development of the Special Theory of Relativity, a profound advance.

Recently some people, especially John Horgan in his book The End of Science (1996), have been making similar claims about how the enterprise of science is complete. My opinion is that they are no more correct than was Michelson. I certainly hope they are wrong, because if they are correct all the fun goes out of physics. In fact, as we shall see, I think there are already a couple of clouds on the horizon. One cloud is the failure of our theories of cosmology to account for recent observations of the universe. The other is the failure of the quark model to produce any truly useful results.

Before we turn to the experiment itself we will consider a "race" between two swimmers.

We have two identical swimmers, 1 and 2, who each swim the same distance away from the raft, to the markers, and then swim back to the raft. The "race" ends in a tie.

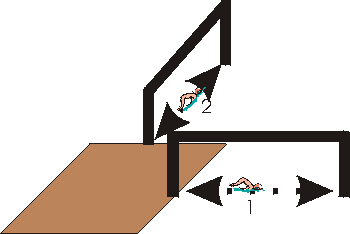
Now the raft and markers are being towed to the left. In this case the race will no longer be a tie. In fact, it is not too hard to show that swimmer 2 wins this race.

A small Flash animation illustrating the above race may be found here.

These notes are intended to be non-mathematical, with the exception of a brief use of Pythagoras theorem about right triangles. However, some people would like to see a little bit of the math. Thus, a proof that swimmer 2 above wins the race may be found here. Below, a further small amount of math will appear, but will always be labelled as a Technical note.

One of the difficulties that students experience in learning about the theories of relativity is that it is easy to ask questions of themselves and/or others that are not well formed. Insisting on complete statements often makes the problems disappear. One common case of sloppy language leading to poorly formed questions involves the concept of speed. If we say, for example, that the swimmers in the above examples swim at 5 km/hr we have not made a complete statement; we should say that the swimmers swim at 5 km/hr with respect to the water. If we are stationary with respect to the water then they swim at 5 km/hr with respect to us. But if we are moving at, say, 5 km/hr with respect to the water in the direction that one of the swimmers is swimming, that swimmer will be stationary relative to us.

Now we consider the Michelson interferometer, shown schematically to the right. The light source is the red star to the left of the figure. The light from it is incident on a half-silvered mirror, which is drawn as a blue line; this is a "crummy" mirror that only reflects one-half of the light incident on it, transmitting the other half. The two light beams then go to good mirrors, drawn as green rectangles, which reflect the light. The reflected light actually follows the same path as the incident beam, although I have drawn them slightly offset. When beam 1 returns to the half-silvered mirror, one half is reflected down; the other half is transmitted back toward the light source but I haven't bothered to draw that ray. Similarly, when beam 2 returns to the half-silvered mirror, one half is transmitted; the other half is reflected towards the source although I haven't drawn that ray either. The two combined beams go from the half-silvered mirror to the detector, which is the yellow object at the bottom of the figure.

If the distance from the half-silvered mirror to mirror 1 is equal to the distance to mirror 2, then when the two rays are re-combined they will have travelled identical distances. Thus, they will be "in phase" and will constructively interfere and we will get a strong signal at the detector. If we slowly move mirror 1 to the right, that ray will be travelling a longer total distance than ray 2; at some point the two rays will be "out of phase" and destructively interfere. Moving mirror 1 a bit further to the right, at some point the two rays will be "in phase" again, giving constructive interference.

Say we have the interferometer adjusted so we are getting constructive interference at the detector. Then the "race" between the two beams of light is essentially a tie. This may remind you of the race of the swimmers above.

Except that if we have the apparatus sitting on the earth, we have to remember that the speed of the earth in its orbit around the sun is on the order of 108,000 km/hr relative to the ether, depending on the season and time of day. So the situation is more like the second race above when the raft is being towed through the water. The interferometer is being "towed" through the ether.

Michelson and Morley did this experiment in the 1880's. The arms of the interferometer were about 1.2 meters long. The apparatus was mounted on a block of marble floating in a pool of mercury to reduce vibrations. They adjusted the interferometer for constructive interference, and then gently rotated the interferometer by 90 degrees.

Given the speed of light as 1,079,253,000 km/hr relative to the ether and the speed of the earth equal to some number like 108,000 km/hr relative to the ether, they calculated that they should easily see the combined beams going through maxima and minima in the interference pattern as they rotated the apparatus.

Except that when they did the experiment, they got no result. The interference pattern did not change!

It was suggested that maybe the speed of the earth due to its rotation on its axis was cancelling its speed due to its orbit around the sun. So they waited 12 hours and repeated the experiment. Again they got no result.

It was suggested that the Earth's motion in orbit around the Sun canceled the other motions. So they waited six months and tried the experiment again. And again they got no result.

It was suggested that maybe the mass of the earth "dragged" the ether along with it. So they hauled the apparatus up on top of a mountain, hoping that the mountain would be sticking up into the ether that was not being dragged by the earth. And again they got no result.

Thus, this attempt to measure the motion of the earth relative to the ether failed.

Lorentz was among many who were very puzzled by this result. He proposed that when an object was moving relative to the ether, its length along its direction of motion would be contracted by just the right amount needed to explain the experimental result. If the length of the object when it is at rest with respect to the ether is L₀, then if is is moving at speed v through the ether its length becomes L given by:

\[L=\sqrt{1-v^2/c^2}L_0\]

where c is the speed of light relative to the ether. If you chose to look at the brief mathematical supplement above, the structure of this equation may look familiar to you.

Einstein "Explains" the Michelson-Morley Experiment

When Einstein was 16, in 1895, he asked himself an interesting question:

"If I pursue a beam of light with the velocity c I should observe such a beam of light as a spatially oscillatory electromagnetic field at rest. However, there seems to be no such thing, whether on the basis of experience or according to [the theory of electricity and magnetism]. From the very beginning it appeared to me intuitively clear that, judged from the standpoint of such an observer, everything would have to happen according to the same laws as for an observer who, relative to the earth, was at rest. For how, otherwise, should the first observer know, i.e.. be able to determine, that he is in a state of uniform motion?" -- As later written by Einstein in "Autobiographical Notes", in Schilpp, ed., Albert Einstein: Philosopher-Scientist.

He continued to work on this question for 10 years with the mixture of concentration and determination that characterized much of his work. He published his answer in 1905:

"... light is always propagated in empty space with a definite velocity c which is independent of the state of [relative] motion of the emitting body .... The introduction of a `luminiferous ether' will be superfluous inasmuch as the view here to be developed will not require an `absolutely stationary space' provided with special properties." -- Annalen Physik 17 (1905).

Put another way, the speed of light is 1,079,253,000 km/hr with respect to all observers.

As we shall see, this one statement is equivalent to all of the Special Theory of Relativity, and everything else is just a consequence.

Notice that the statement also explains the null result of the Michelson-Morley experiment. However, although the evidence is not certain it seems quite likely that in 1905 Einstein was unaware of the experiment (cf. Gerald Holton, "Einstein, Michelson and the 'Crucial' Experiment," which has appeared in Thematic Origins of Scientific Thought, pg. 261. and also in Isis 60, 1969, pg. 133.).

EXPLORING THE CONSEQUENCES OF EINSTEIN'S "EXPLANATION"

Here we will begin to see why Einstein's statement about the constancy of the speed of light leads to all of the strange consequences such as time dilation, length contraction, etc. But first we should take a few moments to carefully explore just what we mean when we say some event occurred at some particular place at some particular time

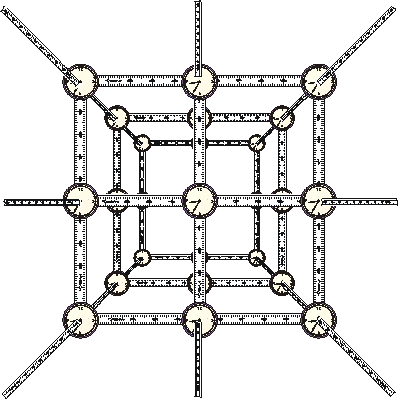We imagine a lattice of meter sticks, such as shown to the right, and at each intersection we place a clock. This lattice represents an inertial frame of reference, and we imagine that we are at rest relative to the lattice.

We synchronise the clocks to the "Reference Clock." To do this correctly requires taking into account that if we are standing by one of the clocks looking at the Reference Clock, the time that we see on the Reference is not the current time, but is the time it was reading when the light we see left the clock. Thus we have to account for the small but finite time it takes light to travel from the Reference Clock to us standing beside another clock. A bit tedious, but fairly straightforward.

We imagine some event occurs. We define its position by where it happened relative to the lattice of meter sticks and we define the time when it happened as the time read by the nearest clock.

Of course, in practice nobody ever does this sort of thing.

Usually we don't bother to draw the whole lattice, but rather represent it by a set of coordinate axes, x and y, and a single clock measuring time t, as shown below. We have also put an observer, whom we shall name Lou, at rest in his coordinate system.

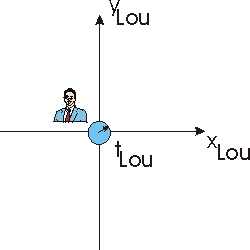
Next we imagine that Lou has a light bulb at the "origin" of his coordinate system. At some time t which we shall call zero he turns on the light. The light moves away from the light bulb at 1,079,253,000 km/hr as measured by Lou's system of rods and clocks. At some time t later the light will form a sphere with the light bulb right at the center.

There are two animations of this situation. One is a "simple" animated gif with a file size of 22k; it may be accessed by clicking here. The other is a Flash animation with a file size of 16k; it may be accessed by clicking here.

Now, Lou has a twin sister Sue, whom we shall assume was born at the same time as Lou (a biological impossibility). Sue has her own lattice of meter sticks and clocks and she is at rest relative to them. Just as for Lou, we represent Sue's rods and clocks as shown below.

Sue is an astronaut, and is in her rocket ship which is traveling at one-half the speed of light to the right relative to Lou. Of course, relative to Sue, Lou is travelling at half the speed of light to the left.

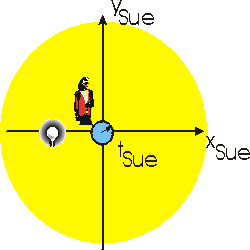
Let us imagine that Sue, traveling at half the speed of light relative to Lou, goes by Lou and he turned on the light bulb just at the moment that Sue passed by it. Sue will call this time zero as measured by her clocks.

Relative to Sue, the light bulb is traveling to the left at half the speed of light. However, because of Einstein's "explanation", the speed of light relative to her is exactly 1,079,253,000 km/hr. Thus, at some later time she will measure that the outer edge of the light forms a perfect sphere with her at the middle.

There are both a animated gif and Flash animation of the above. To access the 18k gif animation click here. To access the 18k Flash animation click here.

There is also a Flash animation of both Sue and Lou. To access the 22k animation click here.

If we think about the above a moment, it is clear that something weird is going on. Lou claims that the light forms a sphere with the light bulb at the center. Sue claims the light forms a sphere with her at the center. But except for the moment when the light bulb was first turned on, the light bulb and Sue are at nowhere near the same place. Evidently the position and time of the outer edge of the sphere as measured by Lou's system of rods and clocks and as measured by Sue's system of rods and clocks are not as our common sense would predict.

Note that the only assumption we have made here is the constancy of the speed of light. Thus, to avoid this sort of weirdness one must come up with another explanation of the null result of the Michelson-Morley experiment.

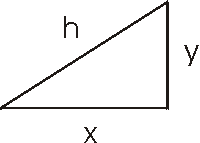We shall close this section by being slightly mathematical. The only mathematics that we shall use is Pythagoras' Theorem for right triangles.

This theorem says that for any right triangle such as the one shown to the right:

x² + y² = h²

Now, when Lou measures the position of the outer edge of the sphere of light he can use Pythagoras' Theorem to calculate the radius r of the sphere:

x²_Lou + y²_Lou = r²_Lou

But the radius at time t is just the speed of the light, c, times the time:

r_Lou = c t_Lou

So:

x²_Lou + y²_Lou = (c t)²_Lou

Notice that we don't need to label c as being the speed of light relative to Lou, since it is the same number for all observers, including Sue.

Now, Sue measures the position of the outer edge of the sphere of light with her rods and clocks and will conclude that:

x²_Sue + y²_Sue = (c t)²_Sue

I will write the relations for Sue and Lou in a form which will be useful later:

x²_Lou + y²_Lou - (c t)²_Lou = 0 = x²_Sue + y²_Sue - (c t)²_Sue

THE PARABLE OF THE SURVEYORS

In this section we do a diversion: a fairy tale.

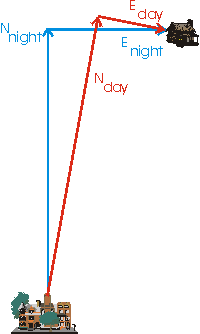
Once upon a time there was a kingdom in which all positions were measured relative to the town square of the capitol.

This kingdom had a sort of strange religion that dictated that all North-South distances were to be measured in sacred units of feet; East-West distances were measured in everyday units of meters.

Despite this religious requirement all positions in the kingdom could be uniquely specified.

There were two schools or surveying in operation. One, the daytime school, used a compass to determine the direction of North. The other, the nighttime school, used the North star to determine the direction of North.

As the sophistication of the measuring instruments increased, people began to notice that the daytime and nighttime measurements didn't quite agree. This is because magnetic North as determined by a compass is not in exactly the same direction as the North star. The figure to the right illustrates, although the actual difference is much less than in the diagram.

Finally, a young fellow named Albert attended both schools of surveying. He was also an irreligious person so he did not take the religious requirement of measuring North-South distances in feet seriously. He converted those North-South distances to everyday units by multiplying by k, the number of meters in a foot. He then discovered that although the daytime and nighttime numbers for the position of a particular place differed slightly, there was a constant:

E²_night + (k N)²_night = E²_day + (k N)²_day

What he is calculating, of course, is the distance squared between the town square and a particular location using Pythagoras' Theorem.

The original source for the above story is E.F. Taylor and J.A. Wheeler, Spacetime Physics (Freeman, 1966), pg. 1.

SPACETIME

In the parable of the surveyors, we converted North-South distances from sacred units of feet to everyday units of meters, and found that for the two rotated reference frames, the daytime and nighttime frames, there was a constant for the position of a particular place in the kingdom relative to the town square:

E²_night + (k N)²_night = E²_day + (k N)²_day

In the section before that Sue and Lou were observing the same sphere of light expanding outwards and saw that here too there was a constant:

x²_Lou + y²_Lou - (c t)²_Lou = x²_Sue + y²_Sue - (c t)²_Sue

Notice the similarity to the surveyor system. Take time, measured in sacred units of seconds, and convert to everyday units of meters by multiplying the time by the speed of light. Take the normal position coordinates x and y plus the time coordinate, square them and combine them: the result is the same number for both Sue and Lou.

Thus we are led to the idea the time is just another coordinate, i.e. that time is the fourth dimension. The fact that there is a minus sign between the square of the normal spatial coordinates and the square of the time coordinates indicates that there is some difference between space and time, but it is not a large difference.

Thus, we tend to write spacetime as a single word as a mnemonic to remind us of all this.

Note that the speed of light, c, is now only a conversion factor for units. If we had started out measuring time in everyday units of meters instead of sacred units of seconds, the speed of light would just be one.

Spacetime Diagrams

The spacetime diagram is a useful visualisation technique.

The time axis is vertical, and of course we have multiplied t by c so we are measuring time in meters, the same as the other coordinates.

An object that is stationary does not have its position change with time: on a spacetime diagram this would be represented by a worldline that is vertical.

If an object is moving, its worldline is not vertical.

For something moving at the speed of light, it moves a distance of, say, 1 meter in a time of 1 meter. Thus the worldline makes an angle of 45 degrees with both the x and ct axes. In the diagram, we have drawn the light cone, representing rays of light that go through the point x=0 and ct=0.

The point x=0 and ct=0 is called the present. Coordinates in spacetime that are inside the light cone and have time coordinates greater than zero are in the future; locations inside the light cone with negative time are in the past.

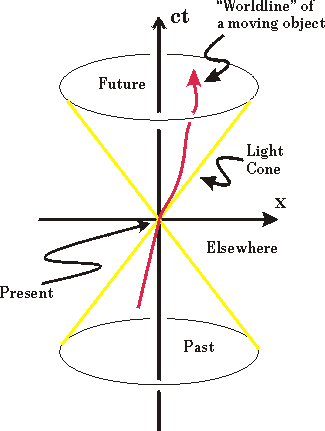
A Spacetime Diagram

Consider that we are located at the present. We know that, for example, we can not know what happened at the star Alpha Centauri yesterday; it is about 4 light years away and since no information can travel faster than the speed of light we will have to wait four years to find out what happened there. Thus the coordinate of Alpha Centauri yesterday, which is outside the light cone, is inaccessible to us. Similarly, we can not get a signal to Alpha Centauri that will arrive tomorrow. Thus the entire region of spacetime outside the light cone is called elsewhere.

The Dimensions of Spacetime

There is a problem with the spacetime diagram: it only has one explicit spatial coordinate x. The way the light cone is drawn suggests, properly, that there is a second spatial coordinate, say y, that points out of the plane of the figure. But what about the third spatial coordinate? It has to be perpendicular to the ct axis and the x axis and the y axis. There is no simple way to draw such a circumstance.

The following figures indicates one way to approach a representation of such a four-dimensional object.

We begin with a zero-dimensional object, a point.

We move the point one unit to the right to generate a one-dimensional line.

Moving the line one unit perpendicular to itself generates a two-dimensional square.

We move the square one unit perpendicular to itself, and we represent the three dimensional cube as shown.

Finally, if the moving of the square down and to the left was used to get from a square to a cube, then we represent moving the cube perpendicular to itself as moving it down and to the right. The result is called a tesseract.

In about 1884 Edwin Abbott wrote a lovely little book called Flatland: a Romance of Many Dimensions; the book has been reprinted many times and is readily available. In it he imagines a world with only two spatial dimensions. One of Flatland's inhabitants, named A. Square, became aware of the existence of a third spatial dimension through an interaction with a higher dimensional being, a Sphere. He attempts to explain this third dimension to the other inhabitants of Flatland, which of course promptly got him put in jail. The difficulties A. Square had in visualising the third spatial dimension is analogous to the difficulties we have in visualising a four-dimensional spacetime. An Flash animation of the interaction of the Sphere with Flatland may be seen here.

More Spacetime Diagrams and Some Discussion

The above spacetime diagram was drawn by Claude Bragdon in 1913 for his book A Primer of Higher Space. In this figure the time axis is horizontal.

Bragdon's "day job" was as an architect. He, along with Abbott, also believed that learning to comprehend a fourth dimension was in some sense equivalent to enlightenment. Bragdon designed many buildings in Rochester New York on which the tesseract can be found.

Einstein wrote when his friend Besso died, "For us believing physicists, the distinction between past, present, and future is illusion, however persistent."

Here is another spacetime diagram, this time from D. Postle, Fabric of the Universe, pg. 106:

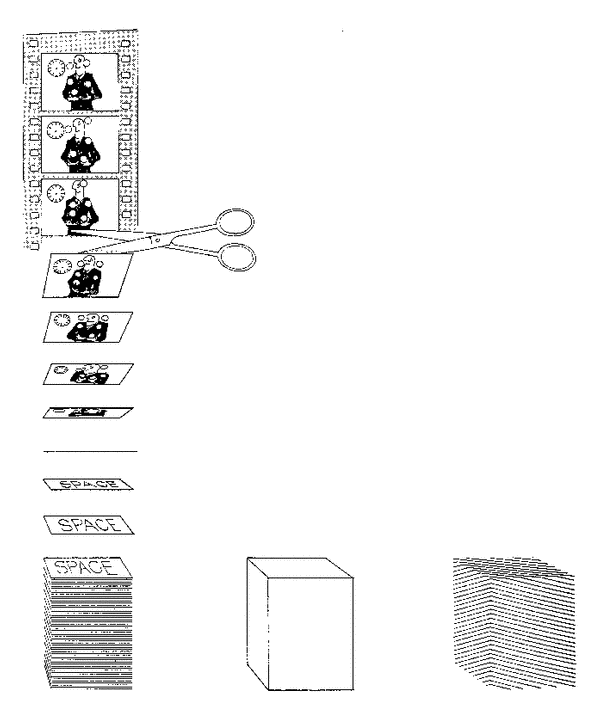
We imagine our worldline in this spacetime diagram. Then, as David Park wrote, "our consciousness crawls along our worldline as a spark burns along a fuse" (in J.T. Fraser et al., eds., The Study of Time, pg. 113). As it crawls up our worldline we discover new slices of spacetime.

Postle included a continuous block of spacetime between the two different ways of slicing it. Quantum Mechanics calls into question whether such a concept is valid.

Imagine we take one of the piles of frames of the movie and shuffle it. The correlation between our consciousness and what it perceives remains the same. So -- would we notice any difference? I don't have any good way to approach a discussion of this question, but it is one that has fascinated me for years.

Louis de Broglie wrote a famous commentary on the worldview of the theory of relativity:

"In space-time, everything which for each of us constitutes the past, the present, and the future is given in block, and the entire collection of events, successive for us, which form the existence of a material particle is represented by a line, the world-line of the particle .... Each observer, as his time passes, discovers, so to speak, new slices of space-time which appear to him as successive aspects of the material world, though in reality this ensemble of events constituting space-time exist prior to his knowledge of them." -- in Albert Einstein: Philosopher-Scientist, pg. 114.

Dogen Zenji seemed to have a similar view 800 years ago. "It is believed by most that time passes; in actual fact it stays where it is. This idea of passing may be called time, but it is an incorrect idea, for since one only sees it as passing, one cannot understand that it stays just where it is. In a word, every being in the entire world is a separate time in one continuum." -- Shobogenzo.

Finally, Arthur I. Miller has argued that this new way of conceiving space and time in Special Relativity is mirrored by the cubist revolution in painting and especially Picasso's "Les Demoiselles d'Avignon" of 1907. He believes that both Einstein and Picasso were influenced by a statement by Poincaré in 1902 that "There is no absolute space … There is no absolute time." Reference: Einstein, Picasso: Space, Time, and the Beauty That Causes Havoc (Basic Books, 2001) ISBN: 0465018599.

Pablo Picasso, Les Demoiselles d'Avignon, 1907.

The Significance of the Minus Sign

In the parable of the surveyors, we saw that:

E²_night + k N²_night = E²_day + k N²_day

where the daytime and nighttime coordinate systems were rotated relative to each other.

For Sue and Lou we saw that:

x²_Lou + y²_Lou - (c t)²_Lou = x²_Sue + y²_Sue - (c t)²_Sue

This is similar to the surveyors, except that there is a minus sign between the spatial coordinates and the time coordinate.

The significance of the minus sign can be shown by drawing the spacetime diagram for Sue and Lou, as shown to the below. Sue's coordinate system is almost rotated relative to Lou's, except that the time axis and the position axis are rotating in opposite directions towards each other.

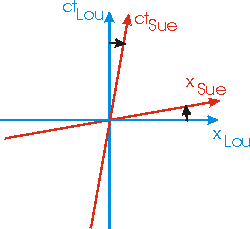
We saw a pre-cursor to this understanding in Postle's spacetime diagram made of movie frames above, where we saw that different observers slice spacetime in different ways.

FURTHER CONSEQUENCES OF EINSTEIN'S "EXPLANATION"

We have just seen that Sue's time and position axes point in different directions than Lou's. This seems to indicate that time is flowing at a different rate for Sue than for Lou, and that her measurements of the distance between two events will be different than his. This is correct, and in this section we shall explore this and other consequences of the Special Theory of Relativity.

Time Dilation

A Flash presentation similar to the discussion of this subsection has been prepared. It requires the Flash player of at least Version 6, and has a file size of 57k. To access the presentation click here.

We imagine that Lou has a light bulb, a mirror, and a light detector: the light bulb and detector are at nearly the same physical location. At some time t equal to zero he turns on the lightbulb. The light travels up to the mirror and is reflected back to the detector.

In the figure to the left, we show the light bulb emitting a light pulse which travels up to the mirror. The figure to the right shows the light traveling from the mirror back to a detector.

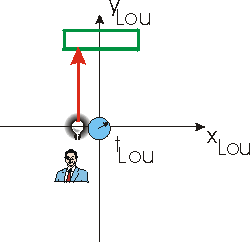
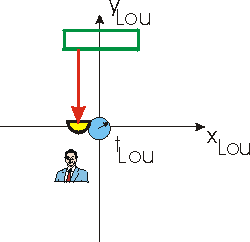
Lou measures the time between the two events, turning on the lightbulb and detecting the return ray with the detector.

We imagine the Sue is moving to the right relative to Lou at, say, half the speed of light. Relative to Sue the light bulb, mirror, and detector are moving to left at half the speed of light. She measures the time between the same two events that Lou measured; she will need two synchronized clocks to do this.

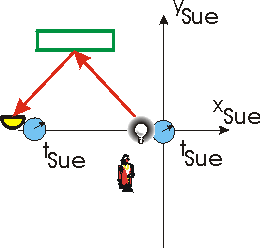
Clearly the light traveled a longer distance from the lightbulb to the detector for Sue than it did for Lou. But the speed of the light is the same for both Sue and Lou. Therefore, the time between the two events as measured by Sue's clocks is greater than the time between the same two events as measured by Lou's clock. We therefore conclude the Sue's clocks are running quickly compared to Lou's clock: Sue's clocks measure a greater elapsed time than Lou's.

This phenomenon is called time dilation: time is flowing at different rates for Sue and Lou.

If it were not for Einstein's "explanation," our common sense would say that if the speed of light relative to Lou is c, then the speed of that same light relative to Sue would have to be larger than c. In fact, if one does the mathematics ignoring Einstein's postulate, the time between the two events is the same for Sue and Lou.

Technical note: if Sue is traveling at a speed v relative to Lou, the mathematical relation between the time between the two events relative to Sue and relative to Lou is given by:

\[t_{Sue} = \frac{t_{Lou}}{\sqrt{1-v^2/c^2}}\]

The mathematics that derives this above relationship may be seen here.

Note that if the speed of light c is infinite, the denominator above becomes one, and the times as measured by Sue and Lou are the same. This is a general feature of Special Relativity: in the limit where the speed of light is effectively infinite these effects are unobservable and common sense prevails.

This prediction of Special Relativity has been experimentally confirmed many times. For example the muon is a type of cosmic ray formed in the upper atmosphere. It is unstable, decaying into an electron and an anti-neutrino. The lifetime of the muon when it is at rest relative to us is 2.196 micro-seconds. The distance from the surface of the Earth to the upper atmosphere where these cosmic rays are formed is about 25 kilometers.

These cosmic ray muons are traveling very close to but not quite at the speed of light. Even if they were traveling at the speed of light, in 2.196 micro-seconds they would only travel 660 meters before they decay. Since they are traveling somewhat less than this speed they will travel somewhat less than 660 meters.

However, when we look at the surface of the Earth we see many of these cosmic ray muons. How can they live long enough to travel 25 kilometers? Because their internal clocks are running slowly compared to our clocks so they are living longer than 2.196 micro-seconds.

Length Contraction

A Flash animation that covers the material of this sub-section has been prepared. It is very similar to this discussion, except for the technical notes and mathematical supplement at the end which are not included. It requires the Flash player of at least version 5 to be installed on your computer. The file size is 37k, and the animation will appear in a separate window. To access the animation click here.

In the previous sub-section we saw that when a muon is traveling at high speeds relative to us, its clock runs slowly compared to ours.

But imagine that we are moving at near-lightspeed towards the surface of the Earth and that a muon formed in the upper atmosphere is stationary relative to us.

Now the muon's clock is running at the same rate as our clocks, so it will live only 2.196 micro-seconds.

Meanwhile the Earth is rushing towards us at near-lightspeed. Further when the Earth's surface reaches us the muon will still not have decayed.

The only way that this is possible is that when the muon was formed, the Earth had to have been less than 660 meters away from us.

Thus we conclude that lengths are contracted when they are moving relative to us. The distance from the Earth to where the muons is formed is 25 km relative to a reference frame stationary on the Earth; the same distance is less than 660 meters in a frame in which the muons are stationary.

The length of an object when it at rest relative to us is called the rest length. If the object is moving relative to us, its length along its direction of motion will be less than the rest length.

Technical note: if we call L₀ the rest length, then the length when it is moving at a speed v relative to us is:

\[L=\sqrt{1-v^2/c^2}L_0\]

Note that this is the same equation Lorentz proposed for the contraction of objects in motion through the ether. Here, though, we interpret the effect quite differently. In any case, physicists sometimes call this Special Relativistic effect the Lorentz contraction.

A final mathematical supplementary document on time dilation and length contraction may be accessed here.

Simultaneity

A Flash animation that covers the material of this sub-section has been prepared. It is very similar to this discussion. It requires the Flash player of at least version 5 to be installed on your computer. The file size is 39k, and the animation will appear in a separate window. To access the animation click here.

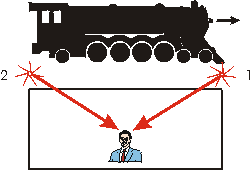Imagine that Lou is standing in the middle of a railway platform as a locomotive goes by at some high speed. Relative to Lou, the platform and the locomotive have the same length. An apparatus, labeled 1, on the front of the locomotive emits a burst of light when it passes the right hand side of the platform. A similar apparatus, labeled 2, is on the back of the locomotive which emits a burst of light when it passes the left hand side of the platform. Lou sees these two flashes of light simultaneously, and since he is in the middle of the platform concludes that the two events occurring at 1 and 2 happened simultaneously.

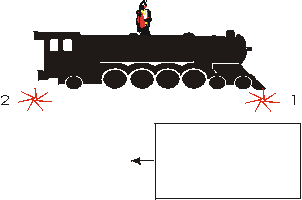Now imagine the Sue is riding on the locomotive. For Lou the length of the locomotive was contracted because of its high speed relative to him; for Sue the locomotive is longer than for Lou. Also, for Sue the platform, traveling from right to left, will have its length contracted.

Thus the two events, the right hand side of the platform passing the front of the locomotive and the left hand side of the platform passing the back of the locomotive, can not happen simultaneously.

Thus, two events that are simultaneous for one observer may not be simultaneous for some other observer. In terms of Postle's movie-frame spacetime diagram above, we would say that if two events are in the same frame of the movie for one observer they will not necessarily be in the same frame for some other observer.

A Little About Language

According to Whorf, the Hopi language cannot even express the idea of absolute simultaneity, that prediction of relativity that so badly tramples on our common sense. But, the Hopi language discusses reality quite differently from English:

"The SAE [Standard Average European language] microcosm has analyzed reality largely in terms of what it calls `things' (bodies and quasibodies) plus modes of extensional but formless existence that it calls `substances' or `matter' .... The Hopi microcosm seems to have analyzed reality largely in terms of EVENTS (or better `eventing'), referred to in two ways, objective and subjective. Objectively, and only if perceptible physical experience, events are expressed mainly as outlines, colors, movements and other perceptive reports. Subjectively, for both the physical and nonphysical, events are considered the expression of invisible intensity factors, on which depend their stability and persistence, or their fugitiveness and proclivities." -- B.L. Whorf, Language, Thought and Reality, pg. 147.

I have a great deal of sympathy with the view that the language with which we think has a close correlation with what we think; this tends to put me in opposition to Chomsky, Pinsky, et al. In any case, I find it interesting that the Hopi language analysis reality in a way so similar to the careful approach to measuring positions and times of events that we set up earlier to discuss relativity, and that the Hopi language and relativity agree on the absence of absolute simultaneity of events.

Relative Speeds

Imagine some object, say a bus, is moving from left to right at 120 km/hr relative to Lou. Also imagine that Sue is moving from left to right at 50 km/hr relative to Lou. Then our common sense tells us that the bus is moving from left to right at 120 - 50 = 70 km/hr relative to Sue.

However, we know from relativity that if instead of a bus moving at some speed less than the speed of light, we think about a light wave moving at c relative to Lou, then the same light wave will move at c relative to Sue.

You will probably not be surprised to learn that our common sense result for the speed of the bus relative to Sue is not quite correct. In fact, according to Special Relativity the speed of the bus relative to Sue is greater than the expected 70 km/hr by about 0.000,000,000,000,35 km/hr, which is 0.003 millimeters per year!

Imagine an unmanned rocket ship that is moving from left to right at three-quarters of the speed of light relative to Lou, and that Sue is moving from left to right at one-half the speed of light relative to Lou. Then relative to Sue the unmanned rocket is moving from left to right at 0.40 times the speed of light, which is noticeably larger than the common sense prediction of 0.75 - 0.50 = 0.25 times the speed of light.

Technical note: if we say that some object is moving at speed u_Lou relative to Lou, and Sue is moving at speed v relative to Lou in the same direction as the object, then the speed of the object relative to Sue is as shown to the right. This equation has the property that if u_Lou equals c, then so does u_Sue regardless of the value of v.

\[u_{Sue}=\frac{u_{Lou}-v}{1-u_{Lou}v/c^2}\]

Mass-Energy Equivalence

Another prediction of Special Relativity is that:

E = m c²

Since we now know that the speed of light is just a conversion factor for units, we can "read" this equation to say that mass and energy are equivalent.

We call the mass of an object when it is at rest relative to us its rest mass. If the object is moving relative to us its mass will be greater than its rest mass.

The relation between the mass m and the speed v of an object is shown below.

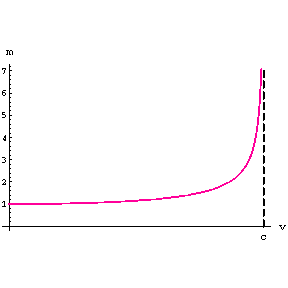
Note that the mass approaches infinity as the speed approaches the speed of light. Thus, it would take infinite energy to accelerate a massive object to the speed of light; another way of saying this is no massive object can ever travel at the speed of light relative to us.

This prediction of Special Relativity has been experimentally confirmed many times. It forms the basis for nuclear energy.

Now we can answer Einstein's original question about what would happen if we pursue a beam of light at the speed of light. The answer is that we can't. No object with a non-zero rest mass can travel at the speed of light relative to any inertial frame of reference, although we can get as close to the speed of light as we wish by providing enough energy. But the light will still always be moving away from us at exactly 1,079,253,000 km/hr.

A supplement about how E = mc² arises in the theory has been prepared. The html version is here and the pdf version is here.

Technical note: if the rest mass is m₀, then the mass m of the object when it is moving at speed v relative to us is:

\[m=\frac{m_0}{\sqrt{1-v^2/c^2}}\]

For light, the denominator is equal to zero since its speed v is equal to the speed of light. By convention, we say that the rest mass of light is zero, so we are dividing 0 by 0. The mathematicians say that this is impossible, but physicists tend to shrug off such pronouncements and say that in this case that the division of the two zeroes works out to be the finite mass-energy of the light.

Probably not Einstein's blackboard in 1905

Tachyons

For a long time people interpreted the material of the previous sub-section to mean that nothing can travel faster than the speed of light. In 1967 Feinberg showed that this is not correct. There is room in the theory for objects whose speed is always greater than c. Feinberg called these hypothetical objects tachyons; the word has the same root as, say, tachometer.

If these objects exist, their properties include:

• It takes infinite energy to slow a tachyon down to the speed of light. Thus c is still a speed limit, but it is a limit from both sides. Ordinary matter always travels at less than the speed of light, light always travels at exactly the speed of light, and tachyons always travel at greater than the speed of light.
• If the tachyon has real energy, its rest mass must be imaginary, i.e. have a factor of the square root of minus 1. This is reasonable, since relativity says that there is no reference frame accessible to us in which the tachyon is at rest.
• If, say, Lou observes a tachyon produced at point A and then traveling to point B where it it detected, for certain states of motion of Sue relative to Lou she would see the tachyon traveling from B to A. Thus it is uncertain which event created the tachyon and which was its detection. Thus tachyons indicate some difficulty with causality.

Many attempts have been made to observe the existence of tachyons; so far all have failed.

One of the attempts to observe tachyons involves a phenomenon called Cerenkov radiation. In order to understand this, we must first realise that when we say that the speed of light is exactly c with respect to all observers, we are referring to the speed of light in a vacuum. When light travels through a medium such as glass, its speed is less than c; for a typical glass the speed of light in it is only about two-thirds of the speed in a vacuum.

It turns out that when an electrically charged object travels through a medium at a speed greater than the speed of light in that medium, a characteristic electromagnetic radiation is emitted. This is Cerenkov radiation. The radiation is shaped roughly like the bow wave from a speedboat.

For the bow wave of a boat, it similarly arises when the speed of the boat through the water is greater than the speed of a water wave.

Nuclear reactors are sometimes encased in water to protect us from the radiation. Often there is a blue glow emitted by charged objects emitted from the reactor that are traveling through the water at a speed greater than the speed of light in the water. This is an example of Cerenkov radiation.

For an electrically charged tachyon traveling through a vacuum, its speed is greater than the speed of light in the vacuum and thus it should similarly emit Cerenkov radiation. Thus, some attempts to observe tachyons has been to look for anamolous Cerenkov radiation.

Superluminal Connections

The reason for the ambiguity in the direction of motion of a tachyon discussed in the previous sub-section arises from the way speeds add for different observers, as discussed in the Relative Speeds sub-section.

Say a tachyon is moving from left to right at 100 times the speed of light relative to Lou. Then if Sue is moving from left to right at a speed greater than 0.01 times the speed of light relative to Lou, the tachyon will be moving from right to left relative to her. If she is moving at 0.1 times the speed of light relative to Lou, the tachyon will be moving at a speed of -111 times the speed of light relative to Sue.

Imagine we wish to send a signal to Alpha Centauri, which is 4.35 light years away from us. If we send the signal at the speed of light, it will take 4.35 years relative to us until the signal gets there. If we could send a signal at, say, 100 times the speed of light then it would arrive in only 0.0435 years.

But if this signal is traveling at this "superluminal" speed relative to us, then for an observer moving towards Alpha Centauri at a speed greater than 0.01 times the speed of light relative to us the signal will be going from Alpha Centauri towards us. So if in our reference frame we say we have sent a signal to Alpha Centauri, there are other frames in which the observers would say that Alpha Centauri has sent a signal to us.

It is these considerations that lead us to say that according to relativity no signal or information can travel faster than the speed of light.

Recently, some controversy has re-ignited on this topic. Further information may be found here.

The "Speed" of Objects

In this sub-section we explore the idea of the speed of objects a little further. I learned this approach to the subject from Brian Greene.

Reference: Brian Greene, The Elegant Universe (Norton, 1999), pg. 47 ff.

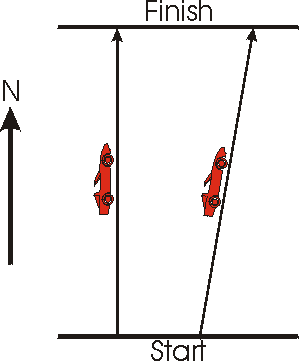
In the figure to the right, we imagine a race between two identical cars. However, although the two cars travel at exactly the same speed relative to the ground, the car on the left wins the race since it travels the shortest path from the Start to the Finish line.

We will find it useful to state that the velocity of the car on the left is only in the North direction, while the velocity of the car on the right has a component in the North direction and another component in the East direction.

Although the example is fairly simple, we are about to use it to make a conceptual leap:

According to the Special Theory of Relativity, all objects travel at the speed of light at all times

We imagine an object that is stationary relative to us. Then its worldline on a spacetime diagram is vertical. We use the fact that time is another dimension of spacetime to say: the object is moving at the speed of light in the direction of the time axis. This is analogous to the car on the left in the above race.

If the object is moving relative to us, then its wordline is not vertical and looks more like the path of the car on the right. But, since it is moving relative to us, the internal clocks of the object run slowly compared to our clocks. Remember that the speed of the object is the "distance" it travels divided by the "time" for it to travel that distance. So, in a fixed amount of "time" the vertical "distance" is less for the moving object but the time for it to travel that distance also becomes less, so their ratio stays the same value, the speed of light.

For objects that travel at the speed of light relative to us, time dilation means their clocks have stopped: they have no component of their speed in the direction of the time axis.

The Lorentz Contraction is Invisible

We have discussed the fact that these relativistic effects violate our common sense because they are unobservable in our everyday life. The reason for the unobservability is that the speed of light is so large compared to everyday speeds that it is effectively infinite.

In 1940 physicist George Gamow published a book, Mr. Tompkins in Wonderland, that imagines a world where the speed of light is only 30 miles per hour. In this world these relativistic effects are readily observable. It has been collected with another of his works dealing with Quantum Mechanics by Cambridge University Press into a book titled Mr. Tompkins in Paperback.

In Wonderland, people observed length contractions, time dilations, etc. in their everyday life. In 1959 Terrell showed that this is not quite correct. When we see the length of a moving rod, we are seeing the light from the back and from the front of the rod that enters our eyes simultaneously. But if the rod is to our left and moving toward us, the light entering our eyes from the back left the rod before the light entering our eyes from the front. Thus it looks longer than it really is. It turns out that this effect cancels the length contraction. So we do not see the length contraction, although careful measurements of the simultaneous positions of the front and back of the rod will indicate that the length is in fact contracted.

In fact, the object will look like it is rotated but not contracted.

A Flash animation demonstrating this effect has been prepared. It requires the Flash 5 player on your computer, and has a file size of 92k. To access the animation click here.

THE TWIN PARADOX

Imagine that Sue blasts off from Earth, travels at high speed to Alpha Centauri, turns around and returns to Earth. Her twin Lou stays on Earth. According to relativity, since Sue's clocks are running slow compared to Lou's, when they rejoin Sue will be younger than Lou. Presumably all the clocks on Sue's rocket ship are running slow, including her internal clocks. So, for example, if she is listening to a CD during her trip the music will sound perfectly normal to her.

Now consider what Sue will observe. From her point of view she is, of course, stationary. But after blast-off Lou moves away from her at some high speed as Alpha Centauri approaches. Then, Alpha Centauri reaches her position and reverses it motion, starting to recede; now Lou and the Earth are getting closer. Throughout Lou has been moving relative to Sue, so his clocks should be running slow compared to Sue's, so he is the one that ends up being younger.

So we have argued that Sue ends up younger, and then have shown that Lou ends up younger. This is often called the twin paradox.

Resolving the paradox is fairly easy. Recall that we have said that we can only do physics in inertial reference frames, frames in which the principle of inertia is true. Although the Earth is in a circular orbit around the Sun and is also rotating on its axis, these accelerations are sufficiently small that we usually treat the Earth as an inertial reference frame.

However, Sue is very far away from being in an inertial reference frame. She experiences high g-forces when she blasts off, experiences yet others when reaches Alpha Centauri and turns around, and yet again when she decelerates and lands on the Earth at the end of her trip. During all these times the principle of inertia is not true. Thus we can not analyse the twin paradox from Sue's reference frame.

We analyse the twins in an inertial reference frame in which, say, Sue is stationary relative to us on her outbound trip. If she is traveling to Alpha Centuari at 99% of the speed of light, then on her outward trip Alpha Centuari is approaching us at 99% of the speed of the light and Lou is receding away from us at 99% of c. When Alpha Centuari reaches us, Sue decelerates, turns around, and chases after Lou. But we're not allowed to go with her: we have to stay in our inertial frame. So relative to us Lou is still receding away at 99% of the speed of light, and Sue is chasing him at an even faster speed than 0.99c. While Sue was stationary relative to us, Lou's clocks were running slow relative to us. But when Sue was chasing after him her clocks were running even slower than Lou's. If one does the math, it turns out that when Sue and Lou are reunited, Sue will end up younger than Lou.

Here is the spacetime diagram in a frame where Lou is stationary:

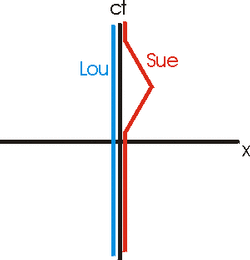
Here is the spacetime diagram in a frame where Sue is stationary on her outward trip.

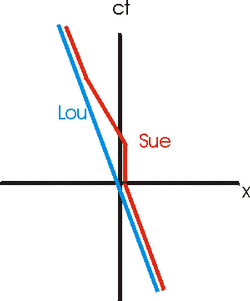
Without doing any of the math, however, we do have what turns out to be a general principle. If we analyze the twins in any inertial reference frame and draw the spacetime diagram, the twin with the longer worldline ends up being the younger twin.

There are many approaches to this paradox. One uses the Relativistic Doppler Effect. A Flash animation of this approach has been prepared; it is somewhat more advanced than the discussion in this document. It requires the Flash 6 player on your computer, and has a file size of 92k. To access the animation, click here.

A FAVORITE PUZZLE

We have a 25 m long pole and a 20 m long barn, both as measured at rest relative to the pole and the barn. We will assume the back wall of the barn is very very strong.

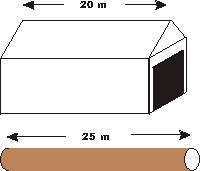
If the pole is moving towards the barn at 70% of the speed of light, its length will be contracted to about 18 m. Thus it clearly fits in the barn, and we can slam the door shut (and run!).

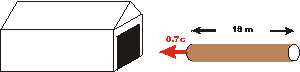
But if we are riding along with the pole, its length is not contracted and is 25 m long. But the barn is contracted and is now about 14 m long. Clearly the pole does not fit in the barn.

Does the pole fit into the barn or not?

CONCLUSION

A famous Zen story: Two Zen monks were arguing about a flag waving in the breeze, and whether it was the flag or the wind that was moving. The Sixth Patriarch of Zen, Hui Neng, overheard; "I suggested it was neither, that what moved was their own mind."

A commentary by Mumon:

Wind, flag, mind moves.
The same understanding.
When the mouth opens
All are wrong.