7.4: The Second Law of Thermodynamics

In a famous lecture entitled The Two Cultures given in 1959, the novelist C. P. Snow commented on a common intellectual attitude of the day - that true education consisted of familiarity with the humanities, literature, arts, music and classics, and that scientists were mere uncultured technicians and ignorant specialists who never read any of the great works of literature. He described how he had often been provoked by such an attitude into asking some of the self-proclaimed intellectuals if they could describe the Second Law of Thermodynamics – a question to which he invariably received a cold and negative response. Yet, he said, he was merely asking something of about the scientific equivalent of "Have you read a work of Shakespeare?"

So I suggest that, if you have never read a work of Shakespeare, take a break for a moment from thermodynamics, go and read A Midsummer Night's Dream, and come back refreshed and ready to complete your well-rounded education by learning the Second Law of Thermodynamics.

We have defined entropy in such a manner that if a quantity of heat dQ is added reversibly to a system at temperature T, the increase in the entropy of the system is dS = dQ/T. We also pointed out that if the heat is transferred irreversibly, dS > dQ/T.

Now consider the following situation (figure VII.1).

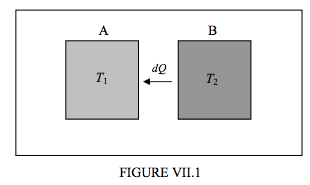
An isolated system consists of two bodies, A at temperature T₁ and B at temperature T₂, such that T₂ >T₁. Heat will eventually be exchanged between the two bodies, and on the whole more heat will be transferred from B to A than from A to B. That is, there will be a net transference of heat, dQ, from B to A. Perhaps this heat is transferred by radiation. Each body is sending forth numerous photons of energy, but there is, on the whole, a net flow of photons from B to A. Or perhaps the two bodies are in contact, and heat is being transferred by conduction. The vibrations in the hot body are more vigorous than those in the cool body, so there will be a net transfer of heat from B to A. However, since the emission of photons in the first case, and the vibrations in the second place, are random, it will be admitted that it is not impossible that at some time more photons may move from A to B than from B to A. Or, in the case of conduction, most of the atoms in A happen to be moving to the right while only a few atoms in B are moving to the left in the course of their oscillations. But, while admitting that this is in principle possible and not outside the laws of physics, it is exceedingly unlikely to happen in practice; indeed so unlikely as hardly to be taken seriously. Thus, in any natural, spontaneous process, without the intervention of an External Intelligence, it is almost certain that there will be a net transfer of heat from B to A. And this process, barring the most unlikely set of circumstances, is irreversible.

The hot body will lose an amount of entropy dQ/T₂, while the cool body will gain an amount of entropy dQ/T₁, which is greater than dQ/T₂. Thus the entropy of the isolated system as a whole increases by dQ/T₁ − dQ/T₂.

From this argument, we readily conclude that any natural, spontaneous and irreversible thermodynamical processes taking place within an isolated system are likely to lead to an increase in entropy of the system. This is perhaps the simplest statement of the Second Law of Thermodynamics.

I have used the phrase "is likely to", although it will be realised that in practice the possibility that the entropy might decrease in a natural process is so unlikely as to be virtually unthinkable, even though it could in principle happen without violating any fundamental laws of physics.

You could regard the Universe as an isolated system. Think of a solid Body sitting somewhere in the Universe. If the Body is hot, it may spontaneously lose heat to the Rest of the Universe. If it is cold, it may spontaneously absorb heat from the Rest of the Universe. Either way, during the course of a spontaneous process, the entropy of the Universe increases.

The transference of heat from a hot body to a cooler body, so that both end at the same intermediate temperature, involves, in effect, the mixing of a set of fast-moving molecules and a set of slow-moving molecules. A similar situation arises if we start with a box having a partition down the middle, and on one side of the partition there is a gas of blue molecules and on the other there is a gas of red molecules. If we remove the partition, eventually the gases will mix into one homogeneous gas. By only a slight extension of the idea of entropy discussed in courses in statistical mechanics, this situation can be described as an increase of entropy – called, in fact, the entropy of mixing. If you saw two photographs, in one of which the blue and red molecules were separated, and in the other the two colours were thoroughly mixed, you would conclude that the latter photograph was probably taken later than the former. But only "probably"; it is conceivable, within the laws of physics, that the velocities of the blue and red molecules separated themselves out without external intervention. This would be allowed perfectly well within the laws of physics. Indeed, if the velocities of all the molecules in the mixed gases were to be reversed, the gases would eventually separate into their two components. But this would seem to be so unlikely as never in practice to happen. The second law says that the entropy of an isolated system is likely (very likely!) to increase with time. Indeed it could be argued that the increase of entropy is the criterion that defines the direction of the arrow of time. (For more on the arrow of time, see Section 15.12 of the notes on Electricity and Magnetism of this series. Also read the article on the arrow of time by Paul Davis, Astronomy & Geophysics (Royal Astronomical Society) 46, 26 (2005). You’ll probably also enjoy H. G. Wells’s The Time Machine.)

Note that, in the example of our two bodies exchanging heat, one loses entropy while the other gains entropy; but the gain by the one is greater than the loss from the other, with the result that there is an increase in the entropy of the system as a whole. The principle of the increase of entropy applies to an isolated system.

In case you have ever wondered (who hasn’t?) how life arose on Earth, you now have a puzzle. Surely the genesis and subsequent evolution of life on Earth represents an increase in order and complexity, and hence a decrease in the entropy of mixing. You may conclude from this that the genesis and subsequent evolution of life on Earth requires Divine Intervention, or Intelligent Design, and that the Second Law of Thermodynamics provides Proof of the Existence of God. Or you may conclude that Earth is not an isolated thermodynamical system. Your choice.