12.11: Surface Energy
( \newcommand{\kernel}{\mathrm{null}\,}\)
For a second example of non-PdV work we shall consider the phenomenon of “surface tension”.
It is well known that a liquid tends to contract to a shape that minimizes its surface area. In the absence of other forces, this means that it will become spherical. The effect is often conveniently described in terms of “surface tension”. We describe the tendency of a surface to contract by drawing an imaginary line in the surface, and we say that the surface to one side of the line pulls the surface of the other, and we call the force per unit length perpendicular to the line the surface tension. It is expressed in dynes per cm or newtons per metre. In this section I shall use the following symbols:
Surface tension: Γ
Area: σ
However, from the point of view of thermodynamics, it is easier to think of surface energy. How much work is needed to increase the surface area? And how is this related to what we have described as “surface tension”? It may be noted in passing that energy per unit area (J m−2) is dimensionally similar to force per unit length (N m−1).
A non-spherical blob of liquid will, under the action of surface tension, contract into a spherical blob – i.e. a blob of least surface area for a given volume. It should not come as a surprise to learn that, at least in principle, as the blob adjusts (in an adiabatic process) to its spherical shape of least surface area, it becomes warmer. Molecules near the surface have a high potential energy. As many of them fall beneath the surface as the surface area is decreased, this potential energy is converted to kinetic energy. Conversely, if a spherical drop is distorted from its spherical shape, it becomes cooler.
We have already pointed out that the surface tension can be regarded as the work required to create new area. Increasing the area will result in a fall in temperature, so, if the temperature is kept constant, some heat must be absorbed from the surroundings, and hence the increase in the internal energy is a little more than the surface tension. It may at first seem surprising that doing work on a liquid, in order to create new surface, results in a fall of temperature, but the work is being used not to increase the kinetic energy of the molecules, but rather to increase their potential energy by pulling them to the surface.
One way in which we can imagine work being done on a liquid to increase its surface area is simply to imagine distorting a spherical drop into a nonspherical shape. Another way, which might lend itself more easily to the sort of thermodynamical analysis we are accustomed to in discussing gases, is to imagine a film of soapy water held in a wire frame, constructed of a fixed U-shaped portion A (see figure XII.1), and a bridge B which we can move in and out, allowing us to do work on the liquid by pulling it to the right, or the liquid to do work by pulling the bridge to the left. We could even refer to these two parts as the “cylinder” A and the “piston” B. A difference between this picture and that of a gas inside a real cylinder is that when we pull the “piston” out, we are doing work on the liquid. Nevertheless, as explained above, the temperature of the liquid then drops. If we allow the film to contract and to pull the “piston” to the left, the temperature will rise.
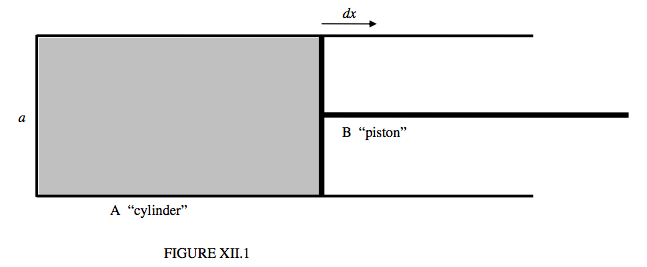
If the width of the “cylinder” is a, the surface tension force with which the liquid is pulling on the “piston” is 2aΓ, where Γ is the surface tension. The factor 2 arises because there are two surfaces, above and below. If we pull the piston to the right through a distance dx, the work we do on the liquid is 2aΓdx. If we do this adiabatically (quickly), the liquid cools. If we do it isothermally (slowly), the liquid has to absorb some heat from its surroundings.
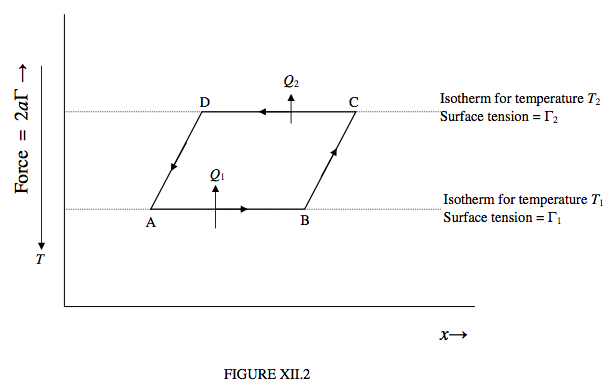
Let us now take the liquid around a Carnot cycle, as shown in figure XII.2. Notice that, as we move the “piston” to the right, provided that the temperature remains constant the surface tension force between the “piston” and the liquid does not change; thus the isotherms are horizontal lines, with the warmer isotherms lying lower than the cooler isotherms.
Let us start by moving the piston to the right, isothermally at a temperature T1, through a distance ∆x, being the portion AB of figure XII.2. The work done on the liquid is 2aΓ1 ∆x, where Γ1 is the surface tension at temperature T1. In order that the process should be isothermal, the liquid has to absorb an amount of heat Q1 from its surroundings. The internal energy increases by 2aΓ1∆x + Q1.
Now expand the liquid further, but this time adiabatically, from B to C. Work is being done on the liquid, but no heat is being absorbed. The temperature drops to T2. The new surface tension is Γ2, which is greater than Γ1, because surface tension generally decreases at warmer temperatures.
Now allow the liquid to contract isothermally at temperature T2, from C to D. The liquid does an amount of work 2aΓ2∆x, and it must lose an amount of heat Q2 (which, as we shall see, is less than Q1) to its surroundings. The internal energy decreases by 2aΓ2∆x + Q2.
Finally, return the liquid to its original state A along the adiabatic path DA. As many molecules on the surface fall back beneath the surface, the temperature rises to its original value T1. Work is being done by the liquid; the work done by the liquid along DA is equal to the work done on it along BC.
The net work done by the liquid around the complete cycle is 2a(Γ2 − Γ1)∆x and the net heat absorbed by the liquid around the cycle is Q1 − Q2. Since there is no change in the internal energy around the cycle (because U is a function of state), these two are equal. Also, there is no change in entropy around the cycle (because S is a function of state), and therefore Q2/T2 = Q1/T1. (This justifies our earlier assertion that Q2 < Q1.)
From these two equations we obtain
Q1T1(T1−T2)=2a(Γ2−Γ1)Δx.
Go to the infinitesimal limit and drop the subscripts, and this becomes
Q=−TdΓdT×2aΔx.
The right hand side is a positive quantity, because dΓdT is negative. We have seen that, in order to create new surface isothermally, heat must be absorbed. What equation 12.12.2 says is that the heat absorbed to create the new area ∆σ = 2a∆x created is equal to Q=−TdΓdT×Δσ.
Now the work required to create the new area is Γ ×∆σ.
Thus the increase in internal energy when new area dσ is created at constant temperature is
ΔU=(Γ−TdΓdT)Δσ.
This will remind you of equation 12.11.1, ΔH=ΔG−TΔ(∂G∂T)P, for the increase in enthalpy of a battery when we add charge to it at constant pressure. This time we are adding new area to a liquid at constant volume.
Here is another way at arriving at the same result: It will remind you of the way in which, in this Chapter, we derived the expression for the Joule coefficient.
The increase in internal energy and Helmholtz functions of a system when we add heat to it and do work on it is given by the familiar equations
dU=TdS−PdV+∑XdY
and
dA=−SdT−PdV+∑XdY.
We are most familiar with them when the term ∑XdY is zero, but in this case we are dealing with a liquid at constant volume, and the one XdY term is Γdσ, so that the equations become
dU=TdS+Γdσ
and
dA=−SdT+Γdσ.
Divide equation 12.12.6 by dσ at constant temperature:
(∂U∂σ)T=T(∂S∂σ)T+Γ.
From equation 12.12.7 obtain a Maxwell relation:
(∂S∂σ)T=−(∂Γ∂T)σ,
except that Γ is in any case independent of σ, so the right hand term is actually a total derivative, dΓ/dT.
Substitute this into equation 12.12.8 and we have the same result as in our previous argument:
(∂U∂σ)T=Γ−TdΓdT.
In summary, the increase in internal energy in creating dσ of new surface at constant temperature is the sum of the work required, Γdσ, and the heat absorbed, −TdΓdTdσ.
Here’s yet another way of getting there! It will remind you of the way in which we derived the expression for the Joule coefficient in Chapter 10. In general the internal energy of a drop of liquid depends on its volume, temperature and surface area:
U=U(V,T,σ).
However, let us ignore the very small change in energy resulting from the very small amount of PdV work that the drop would do if it expands a tiny bit as a result of temperature increase. We shall be concerned only with internal energy as a function of temperature and of surface tension (which may vary with temperature.) Thus, we’ll assume
U=U(T,σ).
For infinitesimal increases in temperature and surface tension, the corresponding increase in the internal energy is
dU=(∂U∂T)σdT+(∂U∂σ)Tdσ.
The internal energy could increase by the addition of heat to the drop, dQ, plus work done on it, dW. The former is TdS, and the latter is +Γdσ. Thus
dU=TdS+Γdσ.
From these we obtain
dS=1T[(∂U∂T)σdT+{(∂U∂σ)T−Γ}dσ].
Since entropy is a function of state, dS is an exact differential, and therefore
1T∂∂σ(∂U∂T)σ=∂∂T[1T(∂U∂σ)T−ΓT].
1T∂2U∂σ∂T=−1T2(∂U∂σ)T+1T∂2U∂T∂σ+ΓT2−1T(∂Γ∂T)σ.
Therefore
(∂U∂σ)T=Γ−T(∂Γ∂T)σ.
Again, we point out that Γ cannot in any case depend on σ, so that last derivative is really a total derivative, so that
(∂U∂σ)T=Γ−TdΓdT
Surface tension generally decreases with temperature, so this equation shows that the increase of internal energy at constant temperature per unit new area is a little greater than the surface tension, as expected.
Can we calculate the fall in temperature if new area is created adiabatically and reversibly (i.e. isentropically)? Yes, because equation 12.12.15 (with dS = 0) tells us that then
(∂U∂T)σdT=−[(∂U∂σ)T−Γ]dσ.
On making use of equation 12.12.19, we obtain
(∂U∂T)σdT=T(∂Γ∂T)σdσ.
We are assuming that the volume is constant so that (∂U∂T)0=CV, and therefore the increase in temperature with area is
dT=TCV(∂Γ∂T)σdσ=TCVdΓdTdσ.
Since dΓdT is generally negative, this means that the temperature falls as the area is increased, as expected. In this equation, if dσ means the increase in area of a sample, in m2, then CV means the heat capacity of that sample, in J K−1.
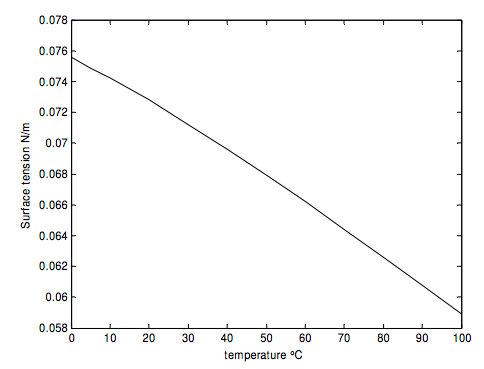
Measurement of the surface tension of a liquid is very sensitive to how clean the surface is, but, for the record, the following figures for the surface tension of clean water in contact with air are taken from the Website www.engineeringtoolbox.com/watersurface-tension-d_597.html
| Temperature - t - (oC) | Surface Tension in contact with air - Γ - (N/m) |
| 0 | 0.0756 |
| 5 | 0.0749 |
| 10 | 0.0742 |
| 20 | 0.0728 |
| 30 | 0.0712 |
| 40 | 0.0696 |
| 50 | 0.0679 |
| 60 | 0.0662 |
| 70 | 0.0644 |
| 80 | 0.0626 |
| 90 | 0.0608 |
| 100 | 0.0589 |
Exercise: A drop of water 1 mm in diameter at 45 °C is broken up into two equal droplets, each half the volume of the original drop. Calculate the change in temperature, and say whether it is cooler or warmer.


