7.1: The van der Waals system

\( \newcommand\bes{\begin{equation}\begin{split}}\)
\( \newcommand\ltwid{\propto}\)
\( \newcommand\ees{\end{split}\end{equation}}\)
\( \newcommand\mib{\mathbf}\)
\( \newcommand\Sa{\textsf a}\)
\( \newcommand\Sb{\textsf b}\)
\( \newcommand\Sc{\textsf c}\)
\( \newcommand\Sd{\textsf d}\)
\( \newcommand\Se{\textsf e}\)
\( \newcommand\Sf{\textsf f}\)
\( \newcommand\Sg{\textsf g}\)
\( \newcommand\Sh{\textsf h}\)
\( \newcommand\Si{\textsf i}\)
\( \newcommand\Sj{\textsf j}\)
\( \newcommand\Sk{\textsf k}\)
\( \newcommand\Sl{\textsf l}\)
\( \newcommand\Sm{\textsf m}\)
\( \newcommand\Sn{\textsf n}\)
\( \newcommand\So{\textsf o}\)
\( \newcommand\Sp{\textsf p}\)
\( \newcommand\Sq{\textsf q}\)
\( \newcommand\Sr{\textsf r}\)
\( \newcommand\Ss{\textsf s}\)
\( \newcommand\St{\textsf t}\)
\( \newcommand\Su{\textsf u}\)
\( \newcommand\Sv{\textsf v}\)
\( \newcommand\Sw{\textsf w}\)
\( \newcommand\Sx{\textsf x}\)
\( \newcommand\Sy{\textsf y}\)
\( \newcommand\Sz{\textsf z}\)
\( \newcommand\SA{\textsf A}\)
\( \newcommand\SB{\textsf B}\)
\( \newcommand\SC{\textsf C}\)
\( \newcommand\SD{\textsf D}\)
\( \newcommand\SE{\textsf E}\)
\( \newcommand\SF{\textsf F}\)
\( \newcommand\SG{\textsf G}\)
\( \newcommand\SH{\textsf H}\)
\( \newcommand\SI{\textsf I}\)
\( \newcommand\SJ{\textsf J}\)
\( \newcommand\SK{\textsf K}\)
\( \newcommand\SL{\textsf L}\)
\( \newcommand\SM{\textsf M}\)
\( \newcommand\SN{\textsf N}\)
\( \newcommand\SO{\textsf O}\)
\( \newcommand\SP{\textsf P}\)
\( \newcommand\SQ{\textsf Q}\)
\( \newcommand\SR{\textsf R}\)
\( \newcommand\SS{\textsf S}\)
\( \newcommand\ST{\textsf T}\)
\( \newcommand\SU{\textsf U}\)
\( \newcommand\SV{\textsf V}\)
\( \newcommand\SW{\textsf W}\)
\( \newcommand\SX{\textsf X}\)
\( \newcommand\SY{\textsf Y}\)
\( \newcommand\SZ{\textsf Z}\)
\( \newcommand\Ha{\hat a}\)
\( \newcommand\Hb{\hat b}\)
\( \newcommand\Hc{\hat c}\)
\( \newcommand\Hd{\hat d}\)
\( \newcommand\He{\hat e}\)
\( \newcommand\Hf{\hat f}\)
\( \newcommand\Hg{\hat g}\)
\( \newcommand\Hh{\hat h}\)
\( \newcommand\Hi{\hat \imath}\)
\( \newcommand\Hj{\hat \jmath}\)
\( \newcommand\Hk{\hat k}\)
\( \newcommand\Hl{\hat l}\)
\( \newcommand\Hm{\hat m}\)
\( \newcommand\Hn{\hat n}\)
\( \newcommand\Ho{\hat o}\)
\( \newcommand\Hp{\hat p}\)
\( \newcommand\Hq{\hat q}\)
\( \newcommand\Hr{\hat r}\)
\( \newcommand\Hs{\hat s}\)
\( \newcommand\Ht{\hat t}\)
\( \newcommand\Hu{\hat u}\)
\( \newcommand\Hv{\hat v}\)
\( \newcommand\Hw{\hat w}\)
\( \newcommand\Hx{\hat x}\)
\( \newcommand\Hy{\hat y}\)
\( \newcommand\Hz{\hat z}\)
\( \newcommand\HA{\hat A}\)
\( \newcommand\HB{\hat B}\)
\( \newcommand\HC{\hat C}\)
\( \newcommand\HD{\hat D}\)
\( \newcommand\HE{\hat E}\)
\( \newcommand\HF{\hat F}\)
\( \newcommand\HG{\hat G}\)
\( \newcommand\HH{\hat H}\)
\( \newcommand\HI{\hat I}\)
\( \newcommand\HJ{\hat J}\)
\( \newcommand\HK{\hat K}\)
\( \newcommand\HL{\hat L}\)
\( \newcommand\HM{\hat M}\)
\( \newcommand\HN{\hat N}\)
\( \newcommand\HO{\hat O}\)
\( \newcommand\HP{\hat P}\)
\( \newcommand\HQ{\hat Q}\)
\( \newcommand\HR{\hat R}\)
\( \newcommand\HS{\hat S}\)
\( \newcommand\HT{\hat T}\)
\( \newcommand\HU{\hat U}\)
\( \newcommand\HV{\hat V}\)
\( \newcommand\HW{\hat W}\)
\( \newcommand\HX{\hat X}\)
\( \newcommand\HY{\hat Y}\)
\( \newcommand\HZ{\hat Z}\)
\( \newcommand\Halpha{\hat\alpha}\)
\( \newcommand\Hbeta{\hat\beta}\)
\( \newcommand\Hgamma{\hat\gamma}\)
\( \newcommand\Hdelta{\hat\delta}\)
\( \newcommand\Hepsilon{\hat\epsilon}\)
\( \newcommand\Hvarepsilon{\hat\varepsilon}\)
\( \newcommand\Hzeta{\hat\zeta}\)
\( \newcommand\Heta{\hat\eta}\)
\( \newcommand\Htheta{\hat\theta}\)
\( \newcommand\Hvartheta{\hat\vartheta}\)
\( \newcommand\Hiota{\hat\iota}\)
\( \newcommand\Hkappa{\hat\kappa}\)
\( \newcommand\Hlambda{\hat\lambda}\)
\( \newcommand\Hmu{\hat\mu}\)
\( \newcommand\Hnu{\hat\nu}\)
\( \newcommand\Hxi{\hat\xi}\)
\( \newcommand\Hom{\hat\omicron}\)
\( \newcommand\Hpi{\hat\pi}\)
\( \newcommand\Hvarpi{\hat\varpi}\)
\( \newcommand\Hrho{\hat\rho}\)
\( \newcommand\Hvarrho{\hat\varrho}\)
\( \newcommand\Hsigma{\hat\sigma}\)
\( \newcommand\Hvarsigma{\hat\varsigma}\)
\( \newcommand\Htau{\var\tau}\)
\( \newcommand\Hupsilon{\hat\upsilon}\)
\( \newcommand\Hphi{\hat\phi}\)
\( \newcommand\Hvarphi{\hat\varphi}\)
\( \newcommand\Hchi{\hat\chi}\)
\( \newcommand\Hxhi{\hat\xhi}\)
\( \newcommand\Hpsi{\hat\psi}\)
\( \newcommand\Homega{\hat\omega}\)
\( \newcommand\HGamma{\hat\Gamma}\)
\( \newcommand\HDelta{\hat\Delta}\)
\( \newcommand\HTheta{\hat\Theta}\)
\( \newcommand\HLambda{\hat\Lambda}\)
\( \newcommand\HXi{\hat\Xi}\)
\( \newcommand\HPi{\hat\Pi}\)
\( \newcommand\HSigma{\hat\Sigma}\)
\( \newcommand\HUps{\hat\Upsilon}\)
\( \newcommand\HPhi{\hat\Phi}\)
\( \newcommand\HPsi{\hat\Psi}\)
\( \newcommand\HOmega{\hat\Omega}\)
\( \newcommand\xhat{\hat\Bx}\)
\( \newcommand\yhat{\hat\By}\)
\( \newcommand\zhat{\hat\Bz}\)
\( \newcommand\ehat{\hat\Be}\)
\( \newcommand\khat{\hat\Bk}\)
\( \newcommand\nhat{\hat\Bn}\)
\( \newcommand\rhat{\hat\Br}\)
\( \newcommand\phihat{\hat\Bphi}\)
\( \newcommand\thetahat{\hat\Btheta}\)
\( \newcommand\MA{\mathbb A}\)
\( \newcommand\MB{\mathbb B}\)
\( \newcommand\MC{\mathbb C}\)
\( \newcommand\MD{\mathbb D}\)
\( \newcommand\ME{\mathbb E}\)
\( \newcommand\MF{\mathbb F}\)
\( \newcommand\MG{\mathbb G}\)
\( \newcommand\MH{\mathbb H}\)
\( \newcommand\MI{\mathbb I}\)
\( \newcommand\MJ{\mathbb J}\)
\( \newcommand\MK{\mathbb K}\)
\( \newcommand\ML{\mathbb L}\)
\( \newcommand\MM{\mathbb M}\)
\( \newcommand\MN{\mathbb N}\)
\( \newcommand\MO{\mathbb O}\)
\( \newcommand\MP{\mathbb P}\)
\( \newcommand\MQ{\mathbb Q}\)
\( \newcommand\MR{\mathbb R}\)
\( \newcommand\MS{\mathbb S}\)
\( \newcommand\MT{\mathbb T}\)
\( \newcommand\MU{\mathbb U}\)
\( \newcommand\MV{\mathbb V}\)
\( \newcommand\MW{\mathbb W}\)
\( \newcommand\MX{\mathbb X}\)
\( \newcommand\MY{\mathbb Y}\)
\( \newcommand\MZ{\mathbb Z}\)
\( \newcommand\CA{\mathcal A}\)
\( \newcommand\CB{\mathcal B}\)
\( \newcommand\CC{\mathcal C}\)
\( \newcommand\CD{\mathcal D}\)
\( \newcommand\CE{\mathcal E}\)
\( \newcommand\CF{\mathcal F}\)
\( \newcommand\CG{\mathcal G}\)
\( \newcommand\CH{\mathcal H}\)
\( \newcommand\CI{\mathcal I}\)
\( \newcommand\CJ{\mathcal J}\)
\( \newcommand\CK{\mathcal K}\)
\( \newcommand\CL{\mathcal L}\)
\( \newcommand\CM{\mathcal M}\)
\( \newcommand\CN{\mathcal N}\)
\( \newcommand\CO{\mathcal O}\)
\( \newcommand\CP{\mathcal P}\)
\( \newcommand\CQ{\mathcal Q}\)
\( \newcommand\CR{\mathcal R}\)
\( \newcommand\CS{\mathcal S}\)
\( \newcommand\CT{\mathcal T}\)
\( \newcommand\CU{\mathcal U}\)
\( \newcommand\CV{\mathcal V}\)
\( \newcommand\CW{\mathcal W}\)
\( \newcommand\CX{\mathcal X}\)
\( \newcommand\CY{\mathcal Y}\)
\( \newcommand\CZ{\mathcal Z}\)
\( \newcommand\Fa{\mathfrak a}\)
\( \newcommand\Fb{\mathfrak b}\)
\( \newcommand\Fc{\mathfrak c}\)
\( \newcommand\Fd{\mathfrak d}\)
\( \newcommand\Fe{\mathfrak e}\)
\( \newcommand\Ff{\mathfrak f}\)
\( \newcommand\Fg{\mathfrak g}\)
\( \newcommand\Fh{\mathfrak h}\)
\( \newcommand\Fi{\mathfrak i}\)
\( \newcommand\Fj{\mathfrak j}\)
\( \newcommand\Fk{\mathfrak k}\)
\( \newcommand\Fl{\mathfrak l}\)
\( \newcommand\Fm{\mathfrak m}\)
\( \newcommand\Fn{\mathfrak n}\)
\( \newcommand\Fo{\mathfrak o}\)
\( \newcommand\Fp{\mathfrak p}\)
\( \newcommand\Fq{\mathfrak q}\)
\( \newcommand\Fr{\mathfrak r}\)
\( \newcommand\Fs{\mathfrak s}\)
\( \newcommand\Ft{\mathfrak t}\)
\( \newcommand\Fu{\mathfrak u}\)
\( \newcommand\Fv{\mathfrak v}\)
\( \newcommand\Fw{\mathfrak w}\)
\( \newcommand\Fx{\mathfrak x}\)
\( \newcommand\Fy{\mathfrak y}\)
\( \newcommand\Fz{\mathfrak z}\)
\( \newcommand\FA{\mathfrak A}\)
\( \newcommand\FB{\mathfrak B}\)
\( \newcommand\FC{\mathfrak C}\)
\( \newcommand\FD{\mathfrak D}\)
\( \newcommand\FE{\mathfrak E}\)
\( \newcommand\FF{\mathfrak F}\)
\( \newcommand\FG{\mathfrak G}\)
\( \newcommand\FH{\mathfrak H}\)
\( \newcommand\FI{\mathfrak I}\)
\( \newcommand\FJ{\mathfrak J}\)
\( \newcommand\FK{\mathfrak K}\)
\( \newcommand\FL{\mathfrak L}\)
\( \newcommand\FM{\mathfrak M}\)
\( \newcommand\FN{\mathfrak N}\)
\( \newcommand\FO{\mathfrak O}\)
\( \newcommand\FP{\mathfrak P}\)
\( \newcommand\FQ{\mathfrak Q}\)
\( \newcommand\FR{\mathfrak R}\)
\( \newcommand\FS{\mathfrak S}\)
\( \newcommand\FT{\mathfrak T}\)
\( \newcommand\FU{\mathfrak U}\)
\( \newcommand\FV{\mathfrak V}\)
\( \newcommand\FW{\mathfrak W}\)
\( \newcommand\FX{\mathfrak X}\)
\( \newcommand\FY{\mathfrak Y}\)
\( \newcommand\FZ{\mathfrak Z}\)
\( \newcommand\Da{\dot a}\)
\( \newcommand\Db{\dot b}\)
\( \newcommand\Dc{\dot c}\)
\( \newcommand\Dd{\dot d}\)
\( \newcommand\De{\dot e}\)
\( \newcommand\Df{\dot f}\)
\( \newcommand\Dg{\dot g}\)
\( \newcommand\Dh{\dot h}\)
\( \newcommand\Di{\dot \imath}\)
\( \newcommand\Dj{\dot \jmath}\)
\( \newcommand\Dk{\dot k}\)
\( \newcommand\Dl{\dot l}\)
\( \newcommand\Dm{\dot m}\)
\( \newcommand\Dn{\dot n}\)
\( \newcommand\Do{\dot o}\)
\( \newcommand\Dp{\dot p}\)
\( \newcommand\Dq{\dot q}\)
\( \newcommand\Dr{\dot r}\)
\( \newcommand\Ds{\dot s}\)
\( \newcommand\Dt{\dot t}\)
\( \newcommand\Du{\dot u}\)
\( \newcommand\Dv{\dot v}\)
\( \newcommand\Dw{\dot w}\)
\( \newcommand\Dx{\dot x}\)
\( \newcommand\Dy{\dot y}\)
\( \newcommand\Dz{\dot z}\)
\( \newcommand\DA{\dot A}\)
\( \newcommand\DB{\dot B}\)
\( \newcommand\DC{\dot C}\)
\( \newcommand\DD{\dot D}\)
\( \newcommand\DE{\dot E}\)
\( \newcommand\DF{\dot F}\)
\( \newcommand\DG{\dot G}\)
\( \newcommand\DH{\dot H}\)
\( \newcommand\DI{\dot I}\)
\( \newcommand\DJ{\dot J}\)
\( \newcommand\DK{\dot K}\)
\( \newcommand\DL{\dot L}\)
\( \newcommand\DM{\dot M}\)
\( \newcommand\DN{\dot N}\)
\( \newcommand\DO{\dot O}\)
\( \newcommand\DP{\dot P}\)
\( \newcommand\DQ{\dot Q}\)
\( \newcommand\DR{\dot R}\)
\( \newcommand\DS{\dot S}\)
\( \newcommand\DT{\dot T}\)
\( \newcommand\DU{\dot U}\)
\( \newcommand\DV{\dot V}\)
\( \newcommand\DW{\dot W}\)
\( \newcommand\DX{\dot X}\)
\( \newcommand\DY{\dot Y}\)
\( \newcommand\DZ{\dot Z}\)
\( \newcommand\Dalpha

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dbeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dgamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Ddelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Depsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dvarepsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dzeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Deta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dtheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dvartheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Diota

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dkappa

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dlambda

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dmu{\dot\mu}\)
\( \newcommand\Dnu{\dot\nu}\)
\( \newcommand\Dxi{\dot\xi}\)
\( \newcommand\Dom{\dot\omicron}\)
\( \newcommand\Dpi{\dot\pi}\)
\( \newcommand\Dvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Drho{\dot\rho}\)
\( \newcommand\Dvarrho{\dot\varrho}\)
\( \newcommand\Dsigma{\dot\sigma}\)
\( \newcommand\Dvarsigma{\dot\varsigma}\)
\( \newcommand\Dtau{\var\tau}\)
\( \newcommand\Dupsilon{\dot\upsilon}\)
\( \newcommand\Dphi{\dot\phi}\)
\( \newcommand\Dvarphi{\dot\varphi}\)
\( \newcommand\Dchi{\dot\chi}\)
\( \newcommand\Dpsi{\dot\psi}\)
\( \newcommand\Domega{\dot\omega}\)
\( \newcommand\DGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DTheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DLambda{\dot\Lambda}\)
\( \newcommand\DXi{\dot\Xi}\)
\( \newcommand\DPi{\dot\Pi}\)
\( \newcommand\DSigma{\dot\Sigma}\)
\( \newcommand\DUps{\dot\Upsilon}\)
\( \newcommand\DPhi{\dot\Phi}\)
\( \newcommand\DPsi{\dot\Psi}\)
\( \newcommand\DOmega{\dot\Omega}\)
\( \newcommand\Va{\vec a}\)
\( \newcommand\Vb{\vec b}\)
\( \newcommand\Vc{\vec c}\)
\( \newcommand\Vd{\vec d}\)
\( \newcommand\Ve{\vec e}\)
\( \newcommand\Vf{\vec f}\)
\( \newcommand\Vg{\vec g}\)
\( \newcommand\Vh{\vec h}\)
\( \newcommand\Vi{\vec \imath}\)
\( \newcommand\Vj{\vec \jmath}\)
\( \newcommand\Vk{\vec k}\)
\( \newcommand\Vl{\vec l}\)
\( \newcommand\Vm{\vec m}\)
\( \newcommand\Vn{\vec n}\)
\( \newcommand\Vo{\vec o}\)
\( \newcommand\Vp{\vec p}\)
\( \newcommand\Vq{\vec q}\)
\( \newcommand\Vr{\vec r}\)
\( \newcommand\Vs{\vec s}\)
\( \newcommand\Vt{\vec t}\)
\( \newcommand\Vu{\vec u}\)
\( \newcommand\Vv{\vec v}\)
\( \newcommand\Vw{\vec w}\)
\( \newcommand\Vx{\vec x}\)
\( \newcommand\Vy{\vec y}\)
\( \newcommand\Vz{\vec z}\)
\( \newcommand\VA{\vec A}\)
\( \newcommand\VB{\vec B}\)
\( \newcommand\VC{\vec C}\)
\( \newcommand\VD{\vec D}\)
\( \newcommand\VE{\vec E}\)
\( \newcommand\VF{\vec F}\)
\( \newcommand\VG{\vec G}\)
\( \newcommand\VH{\vec H}\)
\( \newcommand\VI{\vec I}\)
\( \newcommand\VJ{\vec J}\)
\( \newcommand\VK{\vec K}\)
\( \newcommand\VL{\vec L}\)
\( \newcommand\VM{\vec M}\)
\( \newcommand\VN{\vec N}\)
\( \newcommand\VO{\vec O}\)
\( \newcommand\VP{\vec P}\)
\( \newcommand\VQ{\vec Q}\)
\( \newcommand\VR{\vec R}\)
\( \newcommand\VS{\vec S}\)
\( \newcommand\VT{\vec T}\)
\( \newcommand\VU{\vec U}\)
\( \newcommand\VV{\vec V}\)
\( \newcommand\VW{\vec W}\)
\( \newcommand\VX{\vec X}\)
\( \newcommand\VY{\vec Y}\)
\( \newcommand\VZ{\vec Z}\)
\( \newcommand\Valpha{\vec\alpha}\)
\( \newcommand\Vbeta{\vec\beta}\)
\( \newcommand\Vgamma{\vec\gamma}\)
\( \newcommand\Vdelta{\vec\delta}\)
\( \newcommand\Vepsilon{\vec\epsilon}\)
\( \newcommand\Vvarepsilon{\vec\varepsilon}\)
\( \newcommand\Vzeta{\vec\zeta}\)
\( \newcommand\Veta{\vec\eta}\)
\( \newcommand\Vtheta{\vec\theta}\)
\( \newcommand\Vvartheta{\vec\vartheta}\)
\( \newcommand\Viota{\vec\iota}\)
\( \newcommand\Vkappa{\vec\kappa}\)
\( \newcommand\Vlambda{\vec\lambda}\)
\( \newcommand\Vmu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vnu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vxi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vom

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vtau

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vupsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vchi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vpsi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vomega

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VTheta{\vec\Theta}\)
\( \newcommand\VLambda{\vec\Lambda}\)
\( \newcommand\VXi{\vec\Xi}\)
\( \newcommand\VPi{\vec\Pi}\)
\( \newcommand\VSigma{\vec\Sigma}\)
\( \newcommand\VUps{\vec\Upsilon}\)
\( \newcommand\VPhi{\vec\Phi}\)
\( \newcommand\VPsi{\vec\Psi}\)
\( \newcommand\VOmega{\vec\Omega}\)
\( \newcommand\BA{\mib A}\)
\( \newcommand\BB{\mib B}\)
\( \newcommand\BC{\mib C}\)
\( \newcommand\BD{\mib D}\)
\( \newcommand\BE{\mib E}\)
\( \newcommand\BF{\mib F}\)
\( \newcommand\BG{\mib G}\)
\( \newcommand\BH{\mib H}\)
\( \newcommand\BI{\mib I}}\)
\( \newcommand\BJ{\mib J}\)
\( \newcommand\BK{\mib K}\)
\( \newcommand\BL{\mib L}\)
\( \newcommand\BM{\mib M}\)
\( \newcommand\BN{\mib N}\)
\( \newcommand\BO{\mib O}\)
\( \newcommand\BP{\mib P}\)
\( \newcommand\BQ{\mib Q}\)
\( \newcommand\BR{\mib R}\)
\( \newcommand\BS{\mib S}\)
\( \newcommand\BT{\mib T}\)
\( \newcommand\BU{\mib U}\)
\( \newcommand\BV{\mib V}\)
\( \newcommand\BW{\mib W}\)
\( \newcommand\BX{\mib X}\)
\( \newcommand\BY{\mib Y}\)
\( \newcommand\BZ{\mib Z}\)
\( \newcommand\Ba{\mib a}\)
\( \newcommand\Bb{\mib b}\)
\( \newcommand\Bc{\mib c}\)
\( \newcommand\Bd{\mib d}\)
\( \newcommand\Be{\mib e}\)
\( \newcommand\Bf{\mib f}\)
\( \newcommand\Bg{\mib g}\)
\( \newcommand\Bh{\mib h}\)
\( \newcommand\Bi{\mib i}\)
\( \newcommand\Bj{\mib j}\)
\( \newcommand\Bk{\mib k}\)
\( \newcommand\Bl{\mib l}\)
\( \newcommand\Bm{\mib m}\)
\( \newcommand\Bn{\mib n}\)
\( \newcommand\Bo{\mib o}\)
\( \newcommand\Bp{\mib p}\)
\( \newcommand\Bq{\mib q}\)
\( \newcommand\Br{\mib r}\)
\( \newcommand\Bs{\mib s}\)
\( \newcommand\Bt{\mib t}\)
\( \newcommand\Bu{\mib u}\)
\( \newcommand\Bv{\mib v}\)
\( \newcommand\Bw{\mib w}\)
\( \newcommand\Bx{\mib x}\)
\( \newcommand\By{\mib y}\)
\( \newcommand\Bz{\mib z}\)\)
\( \newcommand\vrh{\varrho}\)
\( \newcommand\vsig{\varsigma}\)
\( \newcommand\ups{\upsilon}\)
\( \newcommand\eps{\epsilon}\)
\( \newcommand\ve{\varepsilon}\)
\( \newcommand\vth{\vartheta}\)
\( \newcommand\vphi{\varphi}\)
\( \newcommand\xhi{\chi}\)
\( \newcommand\Ups{\Upsilon}\)
\( \newcommand\Balpha{\mib\alpha}\)
\( \newcommand\Bbeta{\mib\beta}\)
\( \newcommand\Bgamma{\mib\gamma}\)
\( \newcommand\Bdelta{\mib\delta}\)
\( \newcommand\Beps{\mib\epsilon}\)
\( \newcommand\Bve{\mib\varepsilon}\)
\( \newcommand\Bzeta{\mib\zeta}\)
\( \newcommand\Beta{\mib\eta}\)
\( \newcommand\Btheta{\mib\theta}\)
\( \newcommand\Bvth{\mib\vartheta}\)
\( \newcommand\Biota{\mib\iota}\)
\( \newcommand\Bkappa{\mib\kappa}\)
\( \newcommand\Blambda{\mib\lambda}\)
\( \newcommand\Bmu{\mib\mu}\)
\( \newcommand\Bnu{\mib\nu}\)
\( \newcommand\Bxi{\mib\xi}\)
\( \newcommand\Bom{\mib\omicron}\)
\( \newcommand\Bpi{\mib\pi}\)
\( \newcommand\Bvarpi{\mib\varpi}\)
\( \newcommand\Brho{\mib\rho}\)
\( \newcommand\Bvrh{\mib\varrho}\)
\( \newcommand\Bsigma{\mib\sigma}\)
\( \newcommand\Bvsig{\mib\varsigma}\)
\( \newcommand\Btau{\mib\tau}\)
\( \newcommand\Bups{\mib\upsilon}\)
\( \newcommand\Bphi{\mib\phi}\)
\( \newcommand\Bvphi{\mib\vphi}\)
\( \newcommand\Bchi{\mib\chi}\)
\( \newcommand\Bpsi{\mib\psi}\)
\( \newcommand\Bomega{\mib\omega}\)
\( \newcommand\BGamma{\mib\Gamma}\)
\( \newcommand\BDelta{\mib\Delta}\)
\( \newcommand\BTheta{\mib\Theta}\)
\( \newcommand\BLambda{\mib\Lambda}\)
\( \newcommand\BXi{\mib\Xi}\)
\( \newcommand\BPi{\mib\Pi}\)
\( \newcommand\BSigma{\mib\Sigma}\)
\( \newcommand\BUps{\mib\Upsilon}\)
\( \newcommand\BPhi{\mib\Phi}\)
\( \newcommand\BPsi{\mib\Psi}\)
\( \newcommand\BOmega{\mib\Omega}\)
\( \newcommand\Bxhi{\raise.35ex\hbox{$\Bchi$}}\)
\( \newcommand\RGamma{ \Gamma}\)
\( \newcommand\RDelta{ \Delta}\)
\( \newcommand\RTheta{ \Theta}\)
\( \newcommand\RLambda{ \Lambda}\)
\( \newcommand\RXi{ \Xi}\)
\( \newcommand\RPi{ \Pi}\)
\( \newcommand\RSigma{ \Sigma}\)
\( \newcommand\RUps{ \Upsilon}\)
\( \newcommand\RPhi{ \Phi}\)
\( \newcommand\RPsi{ \Psi}\)
\( \newcommand\ROmega{ \Omega}\)
\( \newcommand\RA{ A}\)
\( \newcommand\RB{ B}\)
\( \newcommand\RC{ C}\)
\( \newcommand\RD{ D}\)
\( \newcommand\RE{ E}\)
\( \newcommand\RF{ F}\)
\( \newcommand\RG{ G}\)
\( \newcommand\RH{ H}\)
\( \newcommand\RI{ I}\)
\( \newcommand\RJ{ J}\)
\( \newcommand\RK{ K}\)
\( \newcommand\RL{ L}\)
\( \newcommand { M}\)
\( \newcommand\RN{ N}\)
\( \newcommand\RO{ O}\)
\( \newcommand\RP{ P}\)
\( \newcommand\RQ{ Q}\)
\( \newcommand\RR{ R}\)
\( \newcommand\RS{ S}\)
\( \newcommand\RT{ T}\)
\( \newcommand\RU{ U}\)
\( \newcommand\RV{ V}\)
\( \newcommand\RW{ W}\)
\( \newcommand\RX{ X}\)
\( \newcommand\RY{ Y}\)
\( \newcommand\RZ{ Z}\)
\( \newcommand\Ra{ a}\)
\( \newcommand\Rb{ b}\)
\( \newcommand\Rc{ c}\)
\( \newcommand\Rd{ d}\)
\( \newcommand\Re{ e}\)
\( \newcommand\Rf{ f}\)
\( \newcommand\Rg{ g}\)
\( \newcommand\Rh{ h}\)
\( \newcommand\Ri{ i}\)
\( \newcommand\Rj{ j}\)
\( \newcommand\Rk{ k}\)
\( \newcommand\Rl{ l}\)
\( \newcommand { m}\)
\( \newcommand\Rn{ n}\)
\( \newcommand\Ro{ o}\)
\( \newcommand\Rp{ p}\)
\( \newcommand\Rq{ q}\)
\( \newcommand\Rr{ r}\)
\( \newcommand\Rs{ s}\)
\( \newcommand\Rt{ t}\)
\( \newcommand\Ru{ u}\)
\( \newcommand\Rv{ v}\)
\( \newcommand\Rw{ w}\)
\( \newcommand\Rx{ x}\)
\( \newcommand\Ry{ y}\)
\( \newcommand\Rz{ z}\)
\( \newcommand\BBA{\boldsymbol\RA}\)
\( \newcommand\BBB{\boldsymbol\RB}\)
\( \newcommand\BBC{\boldsymbol\RC}\)
\( \newcommand\BBD{\boldsymbol\RD}\)
\( \newcommand\BBE{\boldsymbol\RE}\)
\( \newcommand\BBF{\boldsymbol\RF}\)
\( \newcommand\BBG{\boldsymbol\RG}\)
\( \newcommand\BBH{\boldsymbol\RH}\)
\( \newcommand\BBI{\boldsymbol\RI}\)
\( \newcommand\BBJ{\boldsymbol\RJ}\)
\( \newcommand\BBK{\boldsymbol\RK}\)
\( \newcommand\BBL{\boldsymbol\RL}\)
\( \newcommand\BBM{\boldsymbol }\)
\( \newcommand\BBN{\boldsymbol\RN}\)
\( \newcommand\BBO{\boldsymbol\RO}\)
\( \newcommand\BBP{\boldsymbol\RP}\)
\( \newcommand\BBQ{\boldsymbol\RQ}\)
\( \newcommand\BBR{\boldsymbol\RR}\)
\( \newcommand\BBS{\boldsymbol\RS}\)
\( \newcommand\BBT{\boldsymbol\RT}\)
\( \newcommand\BBU{\boldsymbol\RU}\)
\( \newcommand\BBV{\boldsymbol\RV}\)
\( \newcommand\BBW{\boldsymbol\RW}\)
\( \newcommand\BBX{\boldsymbol\RX}\)
\( \newcommand\BBY{\boldsymbol\RY}\)
\( \newcommand\BBZ{\boldsymbol\RZ}\)
\( \newcommand\BBa{\boldsymbol\Ra}\)
\( \newcommand\BBb{\boldsymbol\Rb}\)
\( \newcommand\BBc{\boldsymbol\Rc}\)
\( \newcommand\BBd{\boldsymbol\Rd}\)
\( \newcommand\BBe{\boldsymbol\Re}\)
\( \newcommand\BBf{\boldsymbol\Rf}\)
\( \newcommand\BBg{\boldsymbol\Rg}\)
\( \newcommand\BBh{\boldsymbol\Rh}\}\)
\( \newcommand\BBi{\boldsymbol\Ri}\)
\( \newcommand\BBj{\boldsymbol\Rj}\)
\( \newcommand\BBk{\boldsymbol\Rk}\)
\( \newcommand\BBl{boldsymbol\Rl}\)
\( \newcommand\BBm{\boldsymbol }\)
\( \newcommand\BBn{\boldsymbol\Rn}\)
\( \newcommand\BBo{\boldsymbol\Ro}\)
\( \newcommand\BBp{\boldsymbol\Rp}\)
\( \newcommand\BBq{\boldsymbol\Rq}\)
\( \newcommand\BBr{\boldsymbol\Rr}\)
\( \newcommand\BBs{\boldsymbol\Rs}\)
\( \newcommand\BBt{\boldsymbol\Rt}\)
\( \newcommand\BBu{\boldsymbol\Ru}\)
\( \newcommand\BBv{\boldsymbol\Rv}\)
\( \newcommand\BBw{\boldsymbol\Rw}\)
\( \newcommand\BBx{\boldsymbol\Rx}\)
\( \newcommand\BBy{\boldsymbol\Ry}\)
\( \newcommand\BBz{\boldsymbol\Rz}\)
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
\( \newcommand\bnabla{\boldsymbol{\nabla}}\)
\( \newcommand\Bell{\boldsymbol\ell}\)
\( \newcommand\dbar{\,{\mathchar'26\mkern-12mu d}} \)
\( \newcommand\ns{^\vphantom{*}}\)
\( \newcommand\uar{\uparrow}\)
\( \newcommand\dar{\downarrow}\)
\( \newcommand\impi{\int\limits_{-\infty}^{\infty}\!\!}\)
\( \newcommand\izpi{\int\limits_{0}^{\infty}\!\!}\)
\( \newcommand\etc{\it etc.\/}\)
\( \newcommand\etal{\it et al.\/}\)
\( \newcommand\opcit{\it op. cit.\/}\)
\( \newcommand\ie{\it i.e.\/}\)
\( \newcommand\Ie{\it I.e.\/}\)
\( \newcommand\viz{\it viz.\/}\)
\( \newcommand\eg{\it e.g.\/}\)
\( \newcommand\Eg{\it E.g.\/}\)
\( \newcommand\dbar{\,{\mathchar'26\mkern-12mu d}} \)
\( \def\sss#1{\scriptscriptstyle #1}\)
\( \def\ss#1{\scriptstyle #1}\)
\( \def\ssr#1{\scriptstyle #1}\)
\( \def\ssf#1{\scriptstyle #1}\)
\( \newcommand\NA{N_{\ssr{\!A}}}\)
\( \newcommand\lala{\langle\!\langle}\)
\( \newcommand\rara{\rangle\!\rangle}\)
\( \newcommand\blan{\big\langle}\)
\( \newcommand\bran{\big\rangle}\)
\( \newcommand\Blan{\Big\langle}\)
\( \newcommand\Bran{\Big\rangle}\)
\( \newcommand\intl{\int\limits}\)
\( \newcommand\half{\frac{1}{2}}\)
\( \newcommand\third{\frac{1}{3}}\)
\( \newcommand\fourth{\frac{1}{4}}\)
\( \newcommand\eighth{\frac{1}{8}}\)
\( \newcommand\uar{\uparrow}\)
\( \newcommand\dar{\downarrow}\)
\( \newcommand\undertext#1{$\underline{\hbox{#1}}$}\)
\( \newcommand\Tra{\mathop{\textsf{Tr}}\,}\)
\( \newcommand\det{\mathop{\textsf{det}}\,}\)
\( \def\tket#1{|  #1 \rangle}\)
\( \def\tbra#1{\langle #1|}\)
\( \def\tbraket#1#2{\langle #1  |   #2 \rangle}\)
\( \def\texpect#1#2#3{\langle #1 |   #2  |  #3 \rangle}\)
\( \def\sket#1{|  \, #1 \,  \rangle}\)
\( \def\sbra#1{\langle \,  #1 \, |}\)
\( \def\sbraket#1#2{\langle \, #1  \, |  \, #2 \,  \rangle}\)
\( \def\sexpect#1#2#3{\langle \, #1 \, | \,  #2  \, | \, #3 \, \rangle}\)
\(\def\ket#1{\big| \, #1\, \big\rangle}\)
\( \def\bra#1{\big\langle \, #1 \, \big|}\)
\( \def\braket#1#2{\big\langle \, #1\, \big| \,#2 \,\big\rangle}\)
\( \def\expect#1#2#3{\big\langle\, #1\, \big|\, #2\, \big| \,#3\, \big\rangle}\)
\( \newcommand\pz{\partial}\)
\( \newcommand\pzb{\bar{\partial}}\)
\( \newcommand\svph{\vphantom{\int}}\)
\( \newcommand\vph{\vphantom{\sum_i}}\)
\( \newcommand\bvph{\vphantom{\sum_N^N}}\)
\( \newcommand\nd{^{\vphantom{\dagger}}}\)
\( \newcommand\ns{^{\vphantom{*}}}\)
\( \newcommand\yd{^\dagger}\)
\( \newcommand\zb{\bar z}\)
\( \newcommand\zdot{\dot z}\)
\( \newcommand\zbdot{\dot{\bar z}}\)
\( \newcommand\kB{k_{\sss{B}}}\)
\( \newcommand\kT{k_{\sss{B}}T}\)
\( \newcommand\gtau{g_\tau}\)
\( \newcommand\Htil{\tilde H}\)
\( \newcommand\pairo{(\phi\nd_0,J\nd_0)}\)
\( \newcommand\pairm{(\phi\nd_0,J)}\)
\( \newcommand\pairob{(\Bphi\nd_0,\BJ\nd_0)}\)
\( \newcommand\pairmb{(\Bphi\nd_0,\BJ)}\)
\( \newcommand\pair{(\phi,J)}\)
\( \newcommand\Hz{H\nd_0}\)
\( \newcommand\Ho{H\nd_1}\)
\( \newcommand\Htz{\Htil\nd_0}\)
\( \newcommand\Hto{\Htil\nd_1}\)
\( \newcommand\oc{\omega_\Rc}\)

\(\newcommand \gtwid{\approx}\)

\( \newcommand\index{\textsf{ind}}\)
\( \newcommand\csch{\,{ csch\,}}\)
\( \newcommand\ctnh{\,{ ctnh\,}}\)
\( \newcommand\ctn{\,{ ctn\,}}\)
\( \newcommand\sgn{\,{ sgn\,}}\)
\( \def\tmapright#1{\xrightarrow \limits^{#1}}\)
\( \def\bmapright#1{\xrightarrow\limits_{#1}}\)
\( \newcommand\hfb{\hfill\break}\)
\( \newcommand\Rep{\textsf{Re}\,}\)
\( \newcommand\Imp{\textsf{Im}\,}\)
\( \newcommand\ncdot{\!\cdot\!}\)
\( \def\tmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits^{#1}}\ }\)
\( \def\bmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits_{#1}}\ }\)
\( \newcommand\bsqcap{\mbox{\boldmath{$\sqcap$}}}\)

\( \def\pabc#1#2#3{\left({\pz #1\over\pz #2}\right)\ns_{\!\!#3}}\)
\( \def\spabc#1#2#3{\big({\pz #1\over\pz #2}\big)\ns_{\!#3}}\)
\( \def\qabc#1#2#3{\pz^2\! #1\over\pz #2\,\pz #3}\)
\( \def\rabc#1#2#3#4{(\pz #1,\pz #2)\over (\pz #3,\pz #4)}\)
\( \newcommand\subA{\ns_\ssr{A}}\)
\( \newcommand\subB{\ns_\ssr{B}}\)
\( \newcommand\subC{\ns_\ssr{C}}\)
\( \newcommand\subD{\ns_\ssr{D}}\)
\( \newcommand\subAB{\ns_\ssr{AB}}\)
\( \newcommand\subBC{\ns_\ssr{BC}}\)
\( \newcommand\subCD{\ns_\ssr{CD}}\)
\( \newcommand\subDA{\ns_\ssr{DA}}\)
\( \def\lmapright#1{\ \ \smash{\mathop{\hbox to 55pt{\rightarrowfill}}\limits^{#1}}\ \ }\)
\( \def\enth#1{\RDelta {\textsf H}^0_\Rf[{ #1}]}\)
\( \newcommand\longrightleftharpoons{ \mathop{\vcenter{\hbox{\ooalign{\raise1pt\hbox{$\longrightharpoonup\joinrel$}\crcr  \lower1pt\hbox{$\longleftharpoondown\joinrel$}}}}}}\)
\( \newcommand\longrightharpoonup{\relbar\joinrel\rightharpoonup}\)
\( \newcommand\longleftharpoondown{\leftharpoondown\joinrel\relbar}\)
\( \newcommand\cds{\,\bullet\,}\)
\( \newcommand\ccs{\,\circ\,}\)
\( \newcommand\nsub{_{\vphantom{\dagger}}}\)
\( \newcommand\rhohat{\hat\rho}\)
\( \newcommand\vrhhat{\hat\vrh}\)
\( \newcommand\impi{\int\limits_{-\infty}^\infty\!\!\!}\)
\( \newcommand\brangle{\big\rangle}\)
\( \newcommand\blangle{\big\langle}\)
\( \newcommand\vet{\tilde\ve}\)
\( \newcommand\zbar{\bar z}\)
\( \newcommand\ftil{\tilde f}\)
\( \newcommand\XBE{\RXi\ns_\ssr{BE}}\)
\( \newcommand\XFD{\RXi\ns_\ssr{FD}}\)
\( \newcommand\OBE{\Omega\ns_\ssr{BE}}\)
\( \newcommand\OFD{\Omega\ns_\ssr{FD}}\)
\( \newcommand\veF{\ve\ns_\RF}\)
\( \newcommand\kF{k\ns_\RF}\)
\( \newcommand\kFu{k\ns_{\RF\uar}}\)
\( \newcommand\SZ{\textsf Z}}\) \( \newcommand\kFd{k\ns_{\RF\dar}\)
\( \newcommand\muB{\mu\ns_\ssr{B}}\)
\( \newcommand\mutB{\tilde\mu}\ns_\ssr{B}\)
\( \newcommand\xoN{\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N}\)
\( \newcommand\rok{\Br\ns_1\,,\,\ldots\,,\,\Br\ns_k}\)
\( \newcommand\xhiOZ{\xhi^\ssr{OZ}}\)
\( \newcommand\xhihOZ

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\jhz{\HJ(0)}\)
\( \newcommand\nda{\nd_\alpha}\)
\( \newcommand\ndap{\nd_{\alpha'}}\)
\( \newcommand\labar

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/07:_Mean_Field_Theory_of_Phase_Transitions/7.01:_The_van_der_Waals_system), /content/body/p/span, line 1, column 23

\)
\( \newcommand\msa{m\ns_\ssr{A}}\)
\( \newcommand\msb{m\ns_\ssr{B}}\)
\( \newcommand\mss{m\ns_\Rs}\)
\( \newcommand\HBx{\hat\Bx}\)
\( \newcommand\HBy{\hat\By}\)
\( \newcommand\HBz{\hat\Bz}\)
\( \newcommand\thm{\theta\ns_m}\)
\( \newcommand\thp{\theta\ns_\phi}\)
\( \newcommand\mtil{\widetilde m}\)
\( \newcommand\phitil{\widetilde\phi}\)
\( \newcommand\delf{\delta\! f}\)
\( \newcommand\coll{\bigg({\pz f\over\pz t}\bigg)\nd_{\! coll}}\)
\( \newcommand\stre{\bigg({\pz f\over\pz t}\bigg)\nd_{\! str}}\)
\( \newcommand\idrp{\int\!\!{d^3\!r\,d^3\!p\over h^3}\>}\)
\( \newcommand\vbar{\bar v}\)
\( \newcommand\BCE{\mbox{\boldmath{$\CE$}}\!}\)
\( \newcommand\BCR{\mbox{\boldmath{$\CR$}}\!}\)
\( \newcommand\gla{g\nd_{\RLambda\nd}}\)
\( \newcommand\TA{T\ns_\ssr{A}}\)
\( \newcommand\TB{T\ns_\ssr{B}}\)
\( \newcommand\ncdot{\!\cdot\!}\)
\( \newcommand\NS{N\ns_{\textsf S}}\)

Equation of state

Recall the van der Waals equation of state,

\[\bigg(p+{a\over v^2}\bigg)(v-b)=RT\ ,\]

where \(v=N\ns_{\ssr{A}} V/N\) is the molar volume. Solving for \(p(v,T)\), we have

\[p={RT\over v-b}-{a\over v^2}. \label{pvvdw}\]

Let us fix the temperature \(T\) and examine the function \(p(v)\). Clearly \(p(v)\) is a decreasing function of volume for \(v\) just above the minimum allowed value \(v=b\), as well as for \(v\to\infty\). But is \(p(v)\) a monotonic function for all \(v\in [b,\infty]\)?

We can answer this by computing the derivative,

\[\pabc{p}{v}{T}=\dfrac{2a}{v^3} - \dfrac{RT}{(v-b)^2}. \label{vdwdpdva}\]

Setting this expression to zero for finite \(v\), we obtain the equation¹

\[{2a\over bRT}={u^3\over (u-1)^2} \ , \label{vdwdpdvb}\]

where \(u\equiv v/b\) is dimensionless. It is easy to see that the function \(f(u)=u^3/(u-1)^2\) has a unique minimum for \(u>1\). Setting \(f'(u^*)=0\) yields \(u^*=3\), and so \(f\ns_{min}=f(3)=\frac{27}{4}\). Thus, for \(T>T\ns_\Rc=8a/27bR\), the LHS of Equation \ref{vdwdpdvb} lies below the minimum value of the RHS, and there is no solution. This means that \(p(v,T>T\ns_\Rc)\) is a monotonically decreasing function of \(v\).

At \(T=T\ns_\Rc\) there is a saddle-node bifurcation. Setting \(v\ns_\Rc=b u^*=3b\) and evaluating \(p\ns_\Rc=p(v\ns_\Rc,T\ns_\Rc\)), we have that the location of the critical point for the van der Waals system is

\[p\ns_\Rc={a\over 27\,b^2}\qquad,\qquad v\ns_\Rc=3b\qquad,\qquad T\ns_\Rc={8a\over 27\,bR}.\]

For \(T<T\ns_\Rc\), there are two solutions to Equation \ref{vdwdpdvb}, corresponding to a local minimum and a local maximum of the function \(p(v)\). The locus of points in the \((v,p)\) plane for which \((\pz p/\pz v)\ns_T=0\) is obtained by setting Equation \ref{vdwdpdva} to zero and solving for \(T\), then substituting this into Equation \ref{pvvdw}. The result is

\[p^*(v)={a\over v^2}-{2ab\over v^3}. \label{pstar}\]

Expressed in terms of dimensionless quantities \({\bar p}=p/p\ns_\Rc\) and \({\bar v}=v/v\ns_\Rc\), this equation becomes

\[{\bar p}^*({\bar v})={3\over{\bar v}^2} - {2\over{\bar v}^3}.\]

Figure \(\PageIndex{1}\): Pressure versus molar volume for the van der Waals gas at temperatures in equal intervals from \(T=1.10\, T_\Rc\) (red) to \(T=0.85\,T_\Rc\) (blue). The purple curve is \({\bar p}^*({\bar v})\).

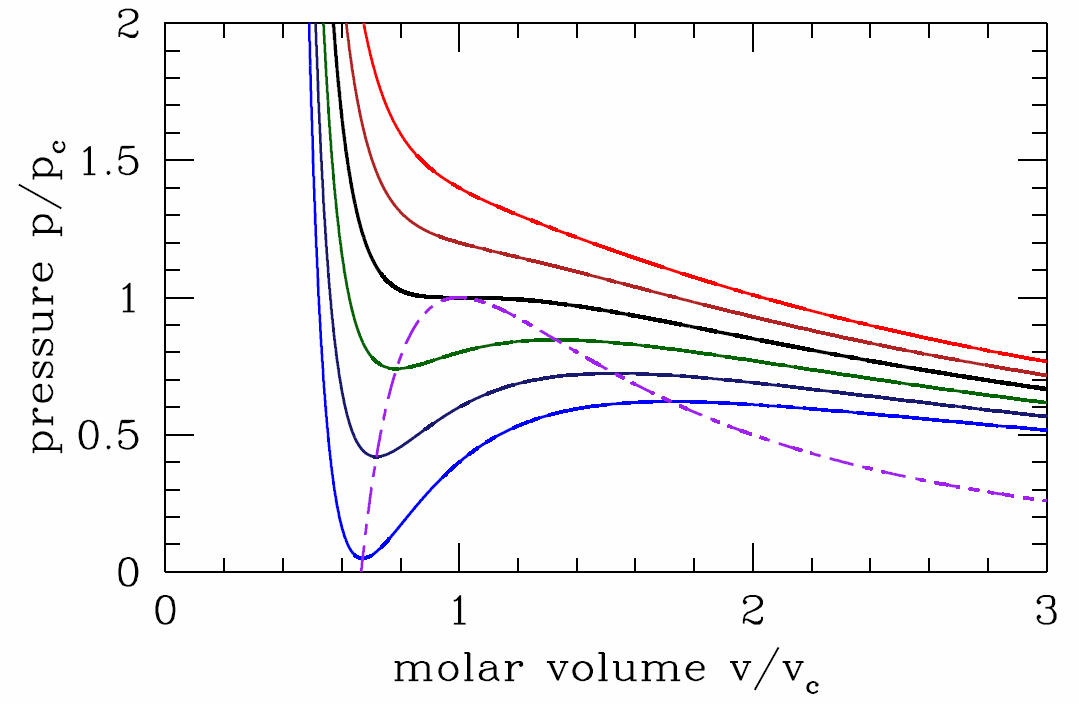
Along the curve \(p=p^*(v)\), the isothermal compressibility, \(\kappa\ns_T=-{1\over v}\big({\pz v\over\pz p}\big)\ns_T\) diverges, heralding a thermodynamic instability. To understand better, let us compute the free energy of the van der Waals system, \(F=E-TS\). Regarding the energy \(E\), we showed back in chapter 2 that

\[\pabc{\ve}{v}{T}=T\pabc{p}{T}{V}-p = {a\over v^2}\ ,\]

which entails

\[\ve(T,v)=\half f RT - {a\over v}\ ,\]

where \(\ve=E/\nu\) is the molar internal energy. The first term is the molar energy of an ideal gas, where \(f\) is the number of molecular freedoms, which is the appropriate low density limit. The molar specific heat is then \(c\ns_V=\big({\pz\ve\over\pz T}\big)\ns_v=\frac{f}{2}R\), which means that the molar entropy is

\[s(T,v)=\int^T\!\!\!\! dT'\ {c\ns_V\over T'} = \frac{f}{2} R \ln(T/T\ns_\Rc) + s\ns_1(v)\ .\]

We then write \(f=\ve-Ts\), and we fix the function \(s\ns_1(v)\) by demanding that \(p=-\big({\pz f\over\pz v}\big)\ns_T\) . This yields \(s\ns_1(v)=R\ln(v-b)+s\ns_0\), where \(s\ns_0\) is a constant. Thus²,

\[f(T,v)=\frac{f}{2} R \, T \, \Big( 1- \ln\!\big(T/T\ns_\Rc\big)\Big) - {a\over v} -R T \ln (v-b) - T s\ns_0\ .\]

Table \(\PageIndex{1}\): van der Waals parameters for some common gases. (Source: Wikipedia)

gas	\(a\ \left({\RL^2\cdot{bar}\over {mol}^2}\right)\)	\(b\ \left({\RL\over{mol}}\right)\)	\(p\ns_\Rc\) (bar)	\(T\ns_\Rc\) (K)	\(v\ns_\Rc\) ( \(\RL/{mol}\))
Acetone	14.09	0.0994	52.82	505.1	0.2982
Argon	1.363	0.03219	48.72	150.9	0.0966
Carbon dioxide	3.640	0.04267	7404	304.0	0.1280
Ethanol	12.18	0.08407	63.83	516.3	0.2522
Freon	10.78	0.0998	40.09	384.9	0.2994
Helium	0.03457	0.0237	2.279	5.198	0.0711
Hydrogen	0.2476	0.02661	12.95	33.16	0.0798
Mercury	8.200	0.01696	1055	1723	0.0509
Methane	2.283	0.04278	46.20	190.2	0.1283
Nitrogen	1.408	0.03913	34.06	128.2	0.1174
Oxygen	1.378	0.03183	50.37	154.3	0.0955
Water	5.536	0.03049	220.6	647.0	0.0915

We know that under equilibrium conditions, \(f\) is driven to a minimum by spontaneous processes. Now suppose that \({\pz^2\! f\over\pz v^2}\big|\nd_T<0\) over some range of \(v\) at a given temperature \(T\). This would mean that one mole of the system at volume \(v\) and temperature \(T\) could lower its energy by rearranging into two half-moles, with respective molar volumes \(v\pm\delta v\), each at temperature \(T\). The total volume and temperature thus remain fixed, but the free energy changes by an amount \(\RDelta f=\half {\pz^2\! f\over\pz v^2} \big|\nd_T(\delta v)^2<0\). This means that the system is unstable – it can lower its energy by dividing up into two subsystems each with different densities ( molar volumes). Note that the onset of stability occurs when

\[{\pz^2 \!f\over\pz v^2}\bigg|\nd_T = -{\pz p\over\pz v}\bigg|\nd_T= {1\over \>v \kappa\ns_p}=0\ ,\]

which is to say when \(\kappa\ns_p=\infty\). As we saw, this occurs at \(p=p^*(v)\), given in Equation [pstar].

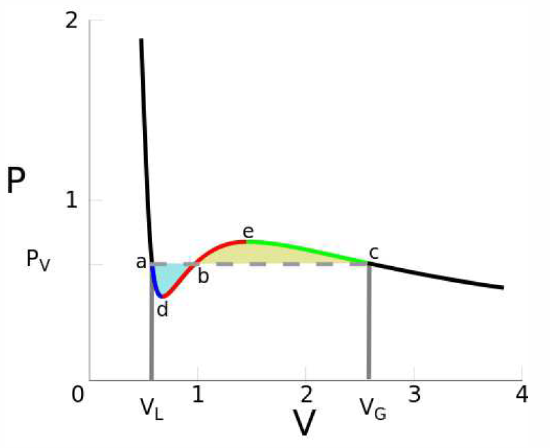
However, this condition, \({\pz^2\! f\over\pz v^2}\big|\nd_T<0\), is in fact too strong. That is, the system can be unstable even at molar volumes where \({\pz^2\! f\over\pz v^2}\big|\nd_T>0\). The reason is shown graphically in Figure \(\PageIndex{2}\). At the fixed temperature \(T\), for any molar volume \(v\) between \(v\ns_{liquid}\equiv v\ns_1\) and \(v\ns_{gas}\equiv v\ns_2\,\), the system can lower its free energy by phase separating into regions of different molar volumes. In general we can write

\[v=(1-x)\,v\ns_1 + x\,v\ns_2\ ,\]

so \(v=v\ns_1\) when \(x=0\) and \(v=v\ns_2\) when \(x=1\). The free energy upon phase separation is simply

\[f=(1-x)\,f\ns_1 + x\,f\ns_2\ ,\]

where \(f\ns_j=f(v\ns_j,T)\). This function is given by the straight black line connecting the points at volumes \(v\ns_1\) and \(v\ns_2\) in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\) Molar free energy \(f(T,v)\) of the van der Waals system \(T=0.85\,T_\Rc\), with dot-dashed black line showing Maxwell construction connecting molar volumes \(v_{1,2}\) on opposite sides of the coexistence curve.

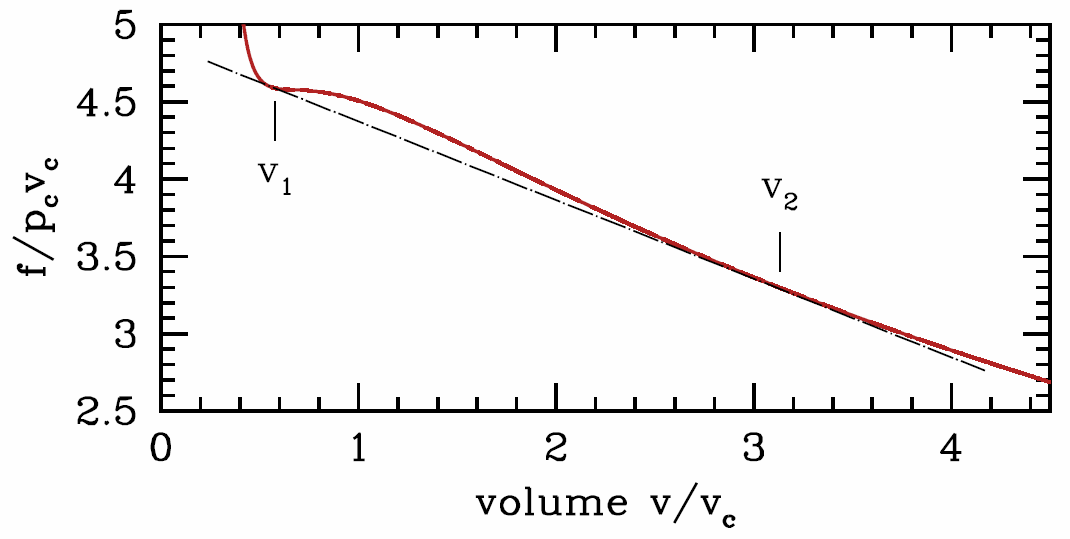
The two equations which give us \(v\ns_1\) and \(v\ns_2\) are

\[{\pz f\over\pz v}\bigg|\nd_{v\ns_1,T}=\ {\pz f\over\pz v}\bigg|\nd_{v\ns_2,T} = {f(T,v\ns_2)-f(T,v\ns_1)\over (v\ns_2-v\ns_1)}\quad.\]

Equivalently, in terms of the pressure, \(p=-{\pz f\over\pz v}\big|\nd_T\) , these equations are equivalent to

\[p(T,v\ns_1)=p(T,v\ns_2)= {1\over v\ns_2-v\ns_1} \int\limits_{v\ns_1}^{v\ns_2}\!\!dv\,p(T,v)\quad.\]

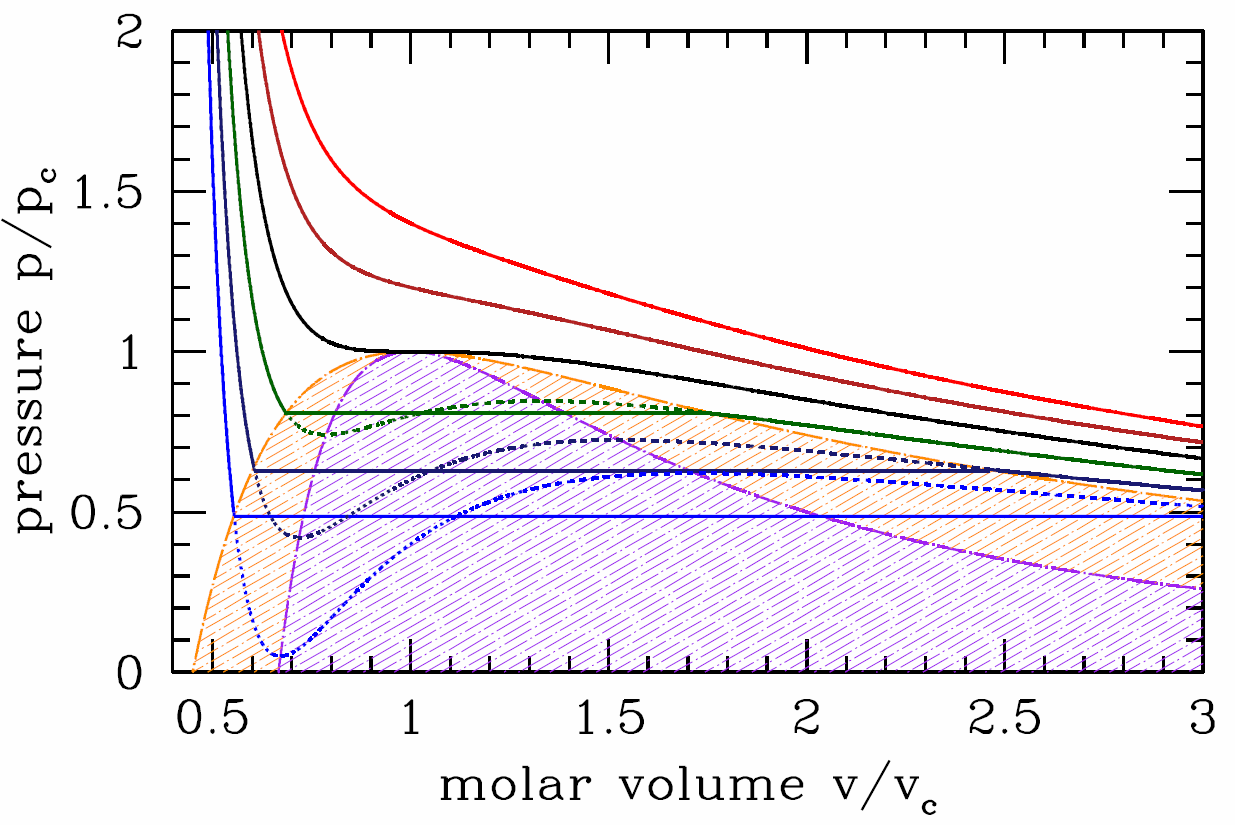
This procedure is known as the Maxwell construction, and is depicted graphically in Figure \(\PageIndex{3}\). When the Maxwell construction is enforced, the isotherms resemble the curves in Figure \(\PageIndex{1}\). In this figure, all points within the purple shaded region have \({\pz^2\!f\over\pz v^2}<0\), hence this region is unstable to infinitesimal fluctuations. The boundary of this region is called the spinodal, and the spontaneous phase separation into two phases is a process known as spinodal decomposition. The dot-dashed orange curve, called the coexistence curve, marks the instability boundary for nucleation. In a nucleation process, an energy barrier must be overcome in order to achieve the lower free energy state. There is no energy barrier for spinodal decomposition – it is a spontaneous process.

Analytic form of the coexistence curve near the critical point

We write \({v\ns_\SL}={v\ns_\Sc}+{w\ns_\SL}\) and \({v\ns_\SG}={v\ns_\Sc}+{w\ns_\SG}\). One of our equations is \(p({v\ns_\Sc}+{w\ns_\SL},T)=p({v\ns_\Sc}+{w\ns_\SG},T)\). Taylor expanding in powers of \({w\ns_\SL}\) and \({w\ns_\SG}\) , we have

\[0 = p\ns_v({v\ns_\Sc},T)\,({w\ns_\SG}-{w\ns_\SL}) + \half\,p\ns_{vv}({v\ns_\Sc},T)\,\big(w_\SG^2-w_\SL^2\big)+ \frac{1}{6}\,p\ns_{vvv}({v\ns_\Sc},T)\,\big(w_\SG^3-w_\SL^3\big) + \ldots\ , \label{coexeqa}\]

where

\[p\ns_v\equiv{\pz p\over\pz v} \quad,\quad p\ns_{vv}\equiv{\pz^2p\over\pz v^2} \quad,\quad p\ns_{vvv}\equiv {\pz^3p\over\pz v^3} \quad , \quad p\ns_{vT}\equiv{\pz^2p\over\pz v\,\pz T}\quad,\quad {etc.}\]

The second equation we write as

\[\int\limits_{w\ns_\SL}^{w\ns_\SG}\!\!dw\>p({v\ns_\Sc}+w,T) = \half({w\ns_\SG}-{w\ns_\SL})\Big(p({v\ns_\Sc}+{w\ns_\SL},T)+p({v\ns_\Sc}+{w\ns_\SG},T)\Big)\ .\]

Expanding in powers of \({w\ns_\SL}\) and \({w\ns_\SG}\), this becomes

\[\begin{split} &p({v\ns_\Sc},T)\,({w\ns_\SG}-{w\ns_\SL}) + \half\,p\ns_v({v\ns_\Sc},T)\,\big(w_\SG^2-w_\SL^2\big) + \frac{1}{6}\,p\ns_{vv}({v\ns_\Sc},T)\,\big(w_\SG^3-w_\SL^3\big)\\ &\hskip1,5in + \frac{1}{24}\,p\ns_{vvv}({v\ns_\Sc},T)\,\big(w_\SG^4-w_\SL^4\big) + \frac{1}{120}\,p\ns_{vvvv}({v\ns_\Sc},T)\,\big(w_\SG^5-w_\SL^5\big) + \ldots \\ &\hskip0.75in=\half({w\ns_\SG}-{w\ns_\SL})\Big\{2\,p({v\ns_\Sc},T) + p\ns_v({v\ns_\Sc},T)\,({w\ns_\SG}+{w\ns_\SL}) + \half\,p\ns_{vv}({v\ns_\Sc},T)\,\big(w_\SG^2+w_\SL^2\big) \\ &\hskip1.7in +\frac{1}{6}\,p\ns_{vvv}({v\ns_\Sc},T)\,\big(w_\SG^3+w_\SL^3\big) + \frac{1}{24}\,p\ns_{vvvv}({v\ns_\Sc},T)\,\big(w_\SG^4+w_\SL^4\big) + \ldots\Big\} \end{split}\]

Subtracting the LHS from the RHS, we find that we can then divide by \(\frac{1}{6}\big(w_\SG^2-w_\SL^2\big)\), resulting in

\[0=p\ns_{vv}({v\ns_\Sc},T) + \half \, p\ns_{vvv}({v\ns_\Sc},T)\,({w\ns_\SG}+{w\ns_\SL}) + \frac{1}{20} \, p\ns_{vvvv}({v\ns_\Sc},T)\, \big(3w_\SG^2+4{w\ns_\SG}{w\ns_\SL}+ 3w_\SL^2\big)+\CO\big(w^3_{\SG,\SL}\big)\ . \label{coexeqb}\]

We now define \(w\ns_\pm\equiv{w\ns_\SG}\pm{w\ns_\SL}\). In terms of these variables, Equations \ref{coexeqa} and \ref{coexeqb} become

\[\begin{split} 0&=p\ns_v({v\ns_\Sc},T)+\half\,p\ns_{vv}({v\ns_\Sc},T)\,w\ns_+ + \frac{1}{8}\,p\ns_{vvv}({v\ns_\Sc},T)\,\big(w_+^2 + \third \, w_-^2\big) + \CO\big(w_\pm^3\big)\vph\\ 0&=p\ns_{vv}({v\ns_\Sc},T) + \half \, p\ns_{vvv}({v\ns_\Sc},T)\,w\ns_+ + \frac{1}{8} \, p\ns_{vvvv}({v\ns_\Sc},T)\,\big(w_+^2 + \frac{1}{5}\,w_-^2\big) +\CO\big(w^3_\pm\big)\ . \end{split}\]

Figure \(\PageIndex{3}\): Maxwell construction in the \((v,p)\) plane. The system is absolutely unstable between volumes \(v_\Rd\) and \(v_\Re\). For \(v\in[v_\Ra,v_\Rd]\) of \(v\in [v_\Re,v_\Rc]\), the solution is unstable with respect to phase separation. Source: Wikipedia.

We now evaluate \(w\ns_\pm\) to order \(T\). Note that \(p\ns_v({v\ns_\Sc},{T\ns_\Sc})=p\ns_{vv}({v\ns_\Sc},{T\ns_\Sc})=0\), since the critical point is an inflection point in the \((v,p)\) plane. Thus, we have \(p\ns_v({v\ns_\Sc},T)=p\ns_{vT}\,\Theta+\CO(\Theta^2)\), where \(T={T\ns_\Sc}+\Theta\) and \(p\ns_{vT}=p\ns_{vT}({v\ns_\Sc},{T\ns_\Sc})\). We can then see that \(w\ns_-\) is of leading order \(\sqrt{-\Theta\,}\), while \(w\ns_+\) is of leading order \(\Theta\). This allows us to write

\[\begin{split} 0&=p\ns_{vT}\,\Theta + \frac{1}{24}\,p\ns_{vvv}\,w_-^2 + \CO(\Theta^2) \vph\\ 0&=p\ns_{vvT}\,\Theta + \half\,p\ns_{vvv}\,w\ns_+ + \frac{1}{40}\,p\ns_{vvvv}\,w_-^2 + \CO(\Theta^2)\ . \end{split}\]

Thus,

\[\begin{split} w\ns_-&=\bigg( {24\, p\ns_{vT} \over p_{vvv} } \bigg)^{\!\!1/2} \sqrt{-\Theta\,} + \ldots\vph \\ w\ns_+&=\bigg({6\,p\ns_{vT}\,p\ns_{vvvv}-10\, p\ns_{vvv}\,p\ns_{vvT}\over 5\, p_{vvv}^2} \bigg)\,\Theta + \ldots \ . \end{split}\]

We then have

\[\begin{split} {w\ns_\SL}&=-\bigg( {6\, p\ns_{vT} \over p_{vvv} } \bigg)^{\!\!1/2} \sqrt{-\Theta\,} +\bigg({3\,p\ns_{vT}\,p\ns_{vvvv}-5\, p\ns_{vvv}\,p\ns_{vvT}\over 5\, p_{vvv}^2} \bigg) \Theta + \CO\big(\Theta^{3/2}\big)\vph \\ {w\ns_\SG}&=\bigg( {6\, p\ns_{vT} \over p_{vvv} } \bigg)^{\!\!1/2} \sqrt{-\Theta\,} +\bigg({3\,p\ns_{vT}\,p\ns_{vvvv}-5\, p\ns_{vvv}\,p\ns_{vvT}\over 5\, p_{vvv}^2} \bigg) \Theta + \CO\big(\Theta^{3/2}\big) \ . \end{split}\]

Suppose we follow along an isotherm starting from the high molar volume (gas) phase. If \(T>{T\ns_\Sc}\), the volume \(v\) decreases continuously as the pressure \(p\) increases. If \(T<{T\ns_\Sc}\), then at the instant the isotherm first intersects the orange boundary curve in Figure \(\PageIndex{4}\), there is a discontinuous change in the molar volume from high (gas) to low (liquid). This discontinuous change is the hallmark of a first order phase transition. Note that the volume discontinuity, \(\RDelta v=w\ns_-\propto ({T\ns_\Sc}-T)^{1/2}\). This is an example of a critical behavior in which the order parameter \(\phi\), which in this case may be taken to be the difference \(\phi={v\ns_\SG}-{v\ns_\SL}\), behaves as a power law in \(\big|T-T\ns_{\!\Rc}\big|\), where \(T\ns_{\!\Rc}\) is the critical temperature. In this case, we have \(\phi(T)\propto ({T\ns_\Sc}-T)_+^\beta\), where \(\beta=\half\) is the exponent, and where \(({T\ns_\Sc}-T)_+\) is defined to be \({T\ns_\Sc}-T\) if \(T<{T\ns_\Sc}\) and \(0\) otherwise. The isothermal compressibility is \(\kappa\ns_T=-v/p\ns_v(v,T)\). This is finite along the coexistence curve – it diverges only along the spinodal. It therefore diverges at the critical point, which lies at the intersection of the spinodal and the coexistence curve.

Figure \(\PageIndex{4}\): Pressure-volume isotherms for the van der Waals system, as in Figure \(\PageIndex{1}\), but corrected to account for the Maxwell construction. The boundary of the purple shaded region is the spinodal line \({\bar p}^*({\bar v})\). The boundary of the orange shaded region is the stability boundary with respect to phase separation.

It is convenient to express the equation of state and the coexistence curve in terms of dimensionless variables. Write

\[{\bar p}={p\over p\ns_\Rc}\quad,\quad {\bar v}={v\over v\ns_\Rc}\quad,\quad {\bar T}={T\over T\ns_\Rc}.\]

The van der Waals equation of state then becomes

\[{\bar p} = {8{\bar T}\over 3{\bar v}-1} - {3\over {\bar v}^2} \ . \label{vdwscaled}\]

Further expressing these dimensionless quantities in terms of distance from the critical point, we write

\[{\bar p}=1+\pi\quad,\quad{\bar v}=1+\eps\quad,\quad{\bar T}=1+t\ .\]

Thus,

\[\pi(\eps,t)={8(1+t)\over 2+3\eps}-{3\over (1+\eps)^2}-1\ .\]

Note that the LHS and the RHS of this equation vanish identically for \((\pi,\eps,t)=(0,0,0)\). We can then write

\[\eps\ns_{\SL,\SG}=\mp \bigg( {6\, \pi\ns_{\eps t} \over \pi\ns_{\eps\eps\eps}} \bigg)^{\!\!1/2} (-t)^{1/2} +\bigg({3\,\pi\ns_{\eps t}\,\pi\ns_{\eps\eps\eps\eps} - 5\, \pi\ns_{\eps\eps\eps}\,\pi\ns_{\eps\eps t}\over 5\, \pi_{\eps\eps\eps}^2} \bigg) t + \CO\big((-t)^{3/2}\big) \ .\]

History of the van der Waals equation

The van der Waals equation of state first appears in van der Waals’ 1873 PhD thesis³, “Over de Continuïteit van den Gas - en Vloeistoftoestand” (“On the continuity of the gas and liquid state”). In his Nobel lecture⁴, van der Waals writes of how he was inspired by Rudolf Clausius’ 1857 treatise on the nature of heat, where it is posited that a gas in fact consists of microscopic particles whizzing around at high velocities. van der Waals reasoned that liquids, which result when gases are compressed, also consist of ’small moving particles’: "Thus I conceived the idea that there is no essential difference between the gaseous and the liquid state of matter…"

Figure [Gugg1945] ‘Universality’ of the liquid-gas transition for eight different atomic and molecular fluids, from E. A. Guggenheim, J. Chem. Phys. 13, 253 (1945). Dimensionless temperature \(T/T_\Rc\) versus dimensionless density \(\rho/\rho_\Rc=v_\Rc/v\) is shown. The van der Waals / mean field theory gives \(\RDelta v =v_{gas}-v_{liquid}\propto (-t)^{1/2}\), while experiments show a result closer to \(\RDelta v \propto (-t)^{1/3}\). Here \(t\equiv {\bar T}-1=(T-T_\Rc)/T_\Rc\) is the dimensionless temperature deviation with respect to the critical point. Image used without permission.

Clausius’ treatise showed how his kinetic theory of heat was consistent with Boyle’s law for gases ( \(pV={constant}\) at fixed temperature). van der Waals pondered why this might fail for the non-dilute liquid phase, and he reasoned that there were two principal differences: inter-particle attraction and excluded volume. These considerations prompted him to posit his famous equation,

\[p={RT\over v-b}-{a\over v^2}.\]

The first term on the RHS accounts for excluded volume effects, and the second for mutual attractions.

In the limiting case of \(p\to\infty\), the molar volume approaches \(v=b\). On physical grounds, one might expect \(b=v\ns_0/\zeta\), where \(v\ns_0=\NA\,\omega\ns_0\) is \(\NA\) times the volume \(\omega\ns_0\) of a single molecule, and the packing fraction is \(\zeta=N\omega\ns_0/V=v\ns_0/v\), which is the ratio of the total molecular volume to the total system volume. In three dimensions, the maximum possible packing fraction is for fcc and hcp lattices, each of which have coordination number \(12\), with \(\zeta\ns_{max}=\frac{\pi}{3\sqrt{2}}=0.74078\). Dense random packing results in \(\zeta\ns_{drp}=0.634\). Expanding the vdW equation of state in inverse powers of \(v\) yields

\[p={RT\over v}+\bigg(b-{a\over RT}\bigg)\cdot{RT\over v^2} + \CO\big(v^{-3}\big)\ ,\]

and we read of the second virial coefficient \(B\ns_2=\big(b-{a\over RT}\big)/\NA\). For hard spheres, \(a=0\), and the result \(B\ns_2=4\omega\ns_0\) from the Mayer cluster expansion corresponds to \(b\ns_{Mayer}=4 v\ns_0\) , which is larger than the result from even the loosest regular sphere packing, that for a cubic lattice, with \(\zeta\ns_\textsf{cub}=\frac{\pi}{6}\).

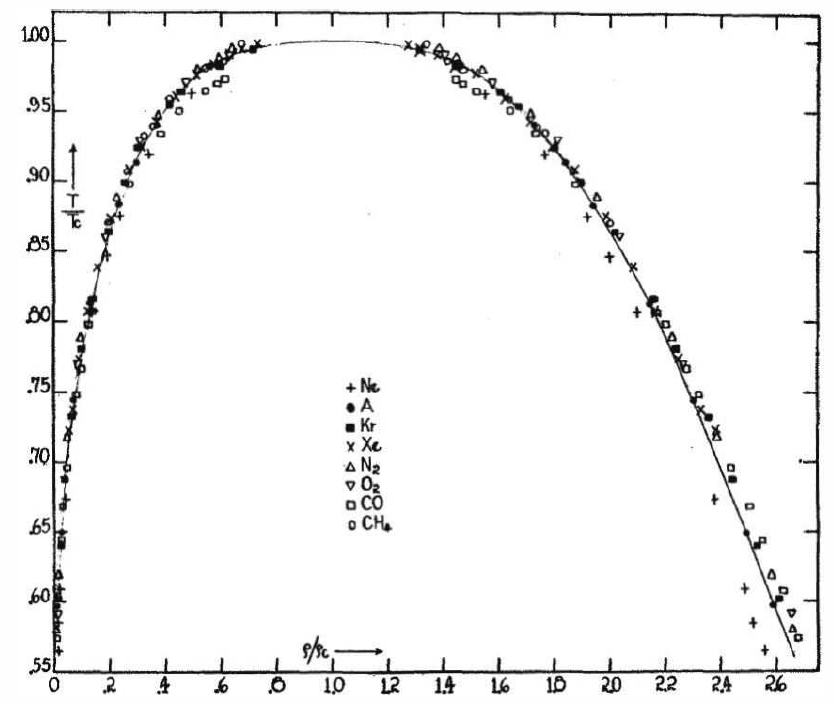
Another of van der Waals’ great achievements was his articulation of the law of corresponding states. Recall that the van der Waals equation of state, when written in terms of dimensionless quantities \({\bar p}=p/p\ns_\Rc\) , \({\bar v}=v/v\ns_\Rc\) , and \({\bar T}=T/T\ns_\Rc\), takes the form of Equation \ref{vdwscaled}. Thus, while the \(a\) and \(b\) parameters are specific to each fluid – see Table \(\PageIndex{1}\) – when written in terms of these scaled dimensionless variables, the equation of state and all its consequent properties ( the liquid-gas phase transition) are universal.

The van der Waals equation is best viewed as semi-phenomenological. Interaction and excluded volume effects surely are present, but the van der Waals equation itself only captures them in a very approximate way. It is applicable to gases, where it successfully predicts features that are not present in ideal systems ( throttling). It is of only qualitative and pedagogical use in the study of fluids, the essential physics of which lies in the behavior of quantities like the pair distribution function \(g(r)\). As we saw in chapter 6, any adequate first principles derivation of \(g(r)\) - a function which can be measured in scattering experiments - involves rather complicated approximation schemes to close the BBGKY hierarchy. Else one must resort to numerical simulations such as the Monte Carlo method. Nevertheless, the lessons learned from the van der Waals system are invaluable and they provide us with a first glimpse of what is going on in the vicinity of a phase transition, and how nonanalytic behavior, such as \(v\ns_\SG-v\ns_\SL\propto (T\ns_\Rc-T)^\beta\) with noninteger exponent \(\beta\) may result due to singularities in the free energy at the critical point.