3.3: Consequences of the Second Law
- Page ID
- 32020
Once we take the second law as an axiom of thermodynamics, there are some important and immediate consequences. The first result is about the efficiency of the Carnot cycle, captured as the following theorem.
Theorem \(\PageIndex{1}\): Carnot Theorem
No engine operating between two specified heat reservoirs can be more efficient than a Carnot engine.
The proof is easy, based on the second law. Consider two engines, say a Carnot engine \(E_1\) and another engine we call \(E_2\), and two reservoirs, at temperatures \(T_H\) and \(T_L\). The Carnot engine is reversible, so we can operate it as a refrigerator. So we can arrange for it to take a certain amount of heat \(Q_1\) from the colder reservoir and deliver an amount \(Q_2 > Q_1\) to the hotter reservoir. This will, of course, require work \(W = Q_2 − Q_1\) to drive the Carnot engine. Now we can arrange for \(E_2\) to take \(Q_2\) from the hotter reservoir, and do an amount of work \(W^\prime = Q_2 − Q^\prime_1\), delivering heat \(Q^\prime_1\) to the colder reservoir. The efficiencies are given by
\[η_1 = \frac{W}{Q_2} , \;\;\;\;\;η_2 = \frac{W^\prime}{Q_2}\]
Assume E2 is more efficient. Then \(η_2 > η_1\), or \(W^\prime > W\). Thus \(Q_1 > Q^\prime_1\) The net amount of heat extracted from the hotter reservoir is zero, the net amount of heat extracted from the colder reservoir is \(Q_1 − Q^\prime_1\). This is entirely converted to work (equal to \(W^\prime − W\)) contradicting the Kelvin statement of the second law. Hence our assumption of \(η_2 > η_1\) must be false, proving the Carnot theorem. Thus we must have \(η_2 ≤ η_1\).
We also have an immediate corollary to the theorem:
Proposition 1
All perfectly reversible engines operating between two given temperatures have the same efficiency.
This is also easily proved. Consider the engine \(E_2\) to be a Carnot engine. From what we have already shown, we will have \(η_2 < η_1\). Since \(E_2\) is reversible, we can change the roles of \(E_1\) and \(E_2\), running \(E_2\) as a refrigerator and \(E_1\) as the engine producing work. In this case, the previous argument would lead to \(η_1 ≤ η_2\). We end up with two statements, \(η_1 ≤ η_2\) and \(η_2 ≤ η_1\). The only solution is \(η_1 = η_2\). Notice that this applies to any reversible engine, since we have not used any specific properties of the Carnot engine except reversibility.
If an engine is irreversible, the previous arguments hold, showing \(η_2 ≤ η_1\), but we cannot get the other inequality because \(E_2\) is not reversible. Thus irreversible engines are less efficient than the Carnot engine.
A second corollary to the theorem is the following:
Proposition 2
The efficiency of a Carnot engine is independent of the working material of the engine.
The arguments so far did not use any specific properties of the material of the Carnot engine, and since all Carnot engines between two given reservoirs have the same efficiency, this clear. We now state another important consequence of the second law
Proposition 3
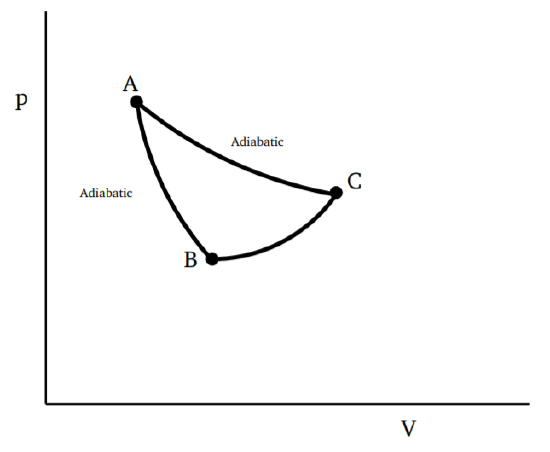
The adiabatics of a thermodynamic system do not intersect.
We prove again by reductio ad absurdum. Assume the adiabatics can intersect, as shown in Fig. 3.3.1. Then we can consider a process going from \(A\) to \(B\) which is adiabatic and hence no heat is absorbed or given up, then a process from \(B\) to \(C\) which absorbs some heat \(\Delta Q\), and then goes back to A along another adiabatic. Since the thermodynamic state at A is restored, the temperature and internal energy are the same at the end as at the beginning, so that \(\Delta U = 0\). Thus by the first law, \(\Delta Q = ∆W\), which means that a certain amount of heat is absorbed and converted entirely to work with no other change in the system. This contradicts the Kelvin statement of the second law. It follows that adiabatics cannot intersect.