2.1: Microscopic Description of a Classical System
( \newcommand{\kernel}{\mathrm{null}\,}\)
This section deals with classical mechanics, not statistical mechanics. But any work that attempts to build macroscopic knowledge from microscopic knowledge—as statistical mechanics does—must begin with a clear and precise statement of what that microscopic knowledge is.
The microscopic description of a physical system has two components: First, “What are the parts of the system? How do they affect each other?”, second, “How are those parts arranged?”. The first question is answered by giving the mechanical parameters1 of the system. The second is answered by giving its dynamical variables. Rather than give formal definitions of these terms, we give two examples.
The earth-moon system. In this system, the mechanical parameters are the mass of the earth, the mass of the moon, and (because the earth and moon interact gravitationally), the gravitational constant G. The dynamical variables are the position and velocity (or momentum) of each body. (Alternative dynamical variables are the position of the center of mass and the separation between the bodies, plus the total momentum of the system and the angular momentum of the two bodies about the center of mass.) You can see from this example that the mechanical parameters give you the knowledge to write down the Hamiltonian for the system, while the dynamical variables are the quantities that change according to the laws governed through that Hamiltonian. The mechanical parameters do not depend upon the initial condition of the system—the dynamical variables do. Often (although not always) the mechanical parameters are timeconstant while the dynamical variables are time-varying.
Helium atoms in a box. It is natural to begin the description by saying that there are N atoms, each of mass m. But this innocent beginning is neither obvious nor precisely correct. By saying that the only thing we need to know about each atom is its mass, we are modeling the atoms as point particles. A more precise model would describe the system as N nuclei and 2N electrons, but then our treatment would necessarily involve quantum mechanics rather than classical mechanics. Furthermore we would not gain anything by this more precise and more difficult description. . . we know from experience that under ordinary conditions the nuclei and electrons do bind themselves together as atoms. Even the more precise description would not result in unassailable rigor, because the nuclei themselves are made up of nucleons and the nucleons of quarks. In fact, a model-building process similar to this one went on unmentioned even in our treatment of the earth-moon system: When we said that we needed to know only the masses of the two bodies, we were assuming (a good but not perfect assumption) that the distribution of matter through the earth and moon was irrelevant to their motion. We will adopt the model that replaces helium atoms by point particles, but you should keep in mind that it is a model.
To continue in our microscopic description, we need to know how the atoms interact with each other. A common model is that atoms interact in a pairwise fashion through some sort of atom-atom interaction potential such as the “Lennard-Jones 6–12 potential”:
atom-atom potential energy =−ar6+br12.
Here the quantities a and b are mechanical parameters.
An important part of the microscopic description of helium atoms in a box is a description of the box. We must know where the walls are located and how the walls interact with the atoms. There are many different models for the wall-atom interaction: common models include the “hard wall” and “soft wall” potential energy functions sketched in figure 2.1.1. But even by assuming that the walls and atoms interact through a potential at all we are making a dramatic and easily overlooked assumption: the assumption of a smooth, non-atomic wall. Real box walls are themselves made up of atoms, which can of course move, so there is no fixed “zero-distance” point as implied by the graphs in the figure. The assumption of fixed, smooth walls implies that when an atom collides with the wall its energy is unchanged, while it is quite possible for the atom to gain or loose some energy while colliding with a real, atomic wall. The assumption of a smooth wall is particularly suspicious, and we will find in chapter 4 that it can be relaxed very profitably.
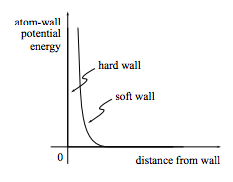
Figure 2.1.1
The final step is to recognize that there might be externally electric, magnetic, or gravitational fields that affect the system. If these external fields are present and relevant they will have to be added to the list of mechanical parameters.
At last we are ready to turn to the dynamical variables for the helium-atoms-in-a-box system. These are (mercifully) easy to describe: they are just the position and momentum of each particle, a total of 2N 3-dimensional vectors. A shorthand name for this information is “point in phase space”. Phase space is an abstract space with one coordinate corresponding to each dynamical variable. Thus in our example the coordinates are the positions and momenta for particle number 1, number 2,. . . number 9,. . . and number N:
(x1,y1,z1,px,1,py,1,x2,y2,z2,pz,2,…x9,y9,z9,px,9,py,9,…xN,yN,zN,px,N,py,N,pz,N).
For a system of N particles, phase space is 6N-dimensional. A single point in phase space gives the position and momentum of every particle in the system.
1The mechanical parameters are sometimes called “parameters in the Hamiltonian”, or “external parameters”, or “fields”.
Time development of a classical system
Given a microscopic description such as either of the two above, what can we do with it? The time development of the system is represented by the motion of a point in phase space. That point will snake through many points in the phase space but all of the points visited will have the same energy.2 Because many points of the given energy will be visited, it is natural to ask whether, in fact, all phase space points corresponding to a given energy will eventually be visited by a system started at any one of those points.
It is easy to find systems for which this statement is false, but all such examples seem to be in one way or another atypical. For example, consider two or three or even many millions of non-interacting particles in a hard-walled box, and start them all traveling straight up and down. They will travel straight up and down forever. The points in phase space with identical energy, but with the particles traveling left and right, will never be visited. This example is atypical because if the particles interacted, even slightly, then they would fall out of the “straight up and down” regions of phase space.
Problems
2.1 (Q) Three-body interactions: microscopic
Make up a problem involving two charged point particles and a polarizable atom.
2.2 Mechanical parameters and dynamical variables
Here is a classical mechanics problem: “A pendulum bob of mass m swings at the end of a cord which runs through a small hole in the ceiling. The cord is being pulled up through the hole so that its length is ell(t)=ℓ0−αt. At time t = 0 the bob is at rest and at angle θ0. Find the subsequent motion of the bob.” Do not solve this problem. Instead, list the mechanical parameters and the dynamical variables that appear in it.
2.3 A Hamiltonian
Write down the total Hamiltonian of a neutral plasma of N protons and N electrons moving in a rectangular box with interior dimensions of Lx × Ly × Lz, assuming that i) any proton or electron interacts with the wall material through a potential energy function
W(d)={W0(1d2−1a2) for d<a0 otherwise
where d is the (perpendicular) distance of the particle in question from the wall, and ii) the system is subject to a uniform electric field in the ˆx direction of magnitude E. List the mechanical parameters that appear in this Hamiltonian, and distinguish them from the dynamical variables.
2.4 (Q) For discussion: Mechanical parameters, dynamical variables, and modeling
List the mechanical parameters and dynamical variables of these systems:
a. Hydrogen molecules enclosed in a sphere.
b. Water molecules in a box.
c. A mixture of hydrogen molecules and helium atoms in a box.
To what extent are you making models as you generate descriptions? To what extent are you making assumptions? (For example, by using non-relativistic classical mechanics.)
2For the earth-moon model, all the points visited will also have the same total momentum and angular momentum, but this is not the case for the helium-in-a-smooth-box model.


