22A: Center of Mass, Moment of Inertia
( \newcommand{\kernel}{\mathrm{null}\,}\)
A mistake that crops up in the calculation of moments of inertia, involves the Parallel Axis Theorem. The mistake is to interchange the moment of inertia of the axis through the center of mass, with the one parallel to that, when applying the Parallel Axis Theorem. Recognizing that the subscript “CM” in the parallel axis theorem stands for “center of mass” will help one avoid this mistake. Also, a check on the answer, to make sure that the value of the moment of inertia with respect to the axis through the center of mass is smaller than the other moment of inertia, will catch the mistake.
Center of Mass
Consider two particles, having one and the same mass m, each of which is at a different position on the x axis of a Cartesian coordinate system.
Common sense tells you that the average position of the material making up the two particles is midway between the two particles. Common sense is right. We give the name “center of mass” to the average position of the material making up a distribution, and the center of mass of a pair of same-mass particles is indeed midway between the two particles.
How about if one of the particles is more massive than the other? One would expect the center of mass to be closer to the more massive particle, and again, one would be right. To determine the position of the center of mass of the distribution of matter in such a case, we compute a weighted sum of the positions of the particles in the distribution, where the weighting factor for a given particle is that fraction, of the total mass, that the particle’s own mass is. Thus, for two particles on the x axis, one of mass m1, at x1, and the other of mass m2, at x2,
the position ˉx of the center of mass is given by
ˉx=m1m1+m2x1+m2m1+m2x2
Note that each weighting factor is a proper fraction and that the sum of the weighting factors is always 1. Also note that if, for instance, m1 is greater than m2, then the position x1 of particle 1 will count more in the sum, thus ensuring that the center of mass is found to be closer to the more massive particle (as we know it must be). Further note that if m1=m2, each weighting factor is 12, as is evident when we substitute m for both m1 and m2 in Equation ???:
ˉx=mm+mx1+mm+mx2
ˉx=12x1+12x2
ˉx=x1+x22
The center of mass is found to be midway between the two particles, right where common sense tells us it has to be.
The Center of Mass of a Thin Rod
Quite often, when the finding of the position of the center of mass of a distribution of particles is called for, the distribution of particles is the set of particles making up a rigid body. The easiest rigid body for which to calculate the center of mass is the thin rod because it extends in only one dimension. (Here, we discuss an ideal thin rod. A physical thin rod must have some nonzero diameter. The ideal thin rod, however, is a good approximation to the physical thin rod as long as the diameter of the rod is small compared to its length.)
In the simplest case, the calculation of the position of the center of mass is trivial. The simplest case involves a uniform thin rod. A uniform thin rod is one for which the linear mass density μ, the mass-per-length of the rod, has one and the same value at all points on the rod. The center of mass of a uniform rod is at the center of the rod. So, for instance, the center of mass of a uniform rod that extends along the x axis from x=0 to x=L is at (L/2, 0).
The linear mass density μ, typically called linear density when the context is clear, is a measure of how closely packed the elementary particles making up the rod are. Where the linear density is high, the particles are close together.
To picture what is meant by a non-uniform rod, a rod whose linear density is a function of position, imagine a thin rod made of an alloy consisting of lead and aluminum. Further imagine that the percentage of lead in the rod varies smoothly from 0% at one end of the rod to 100% at the other. The linear density of such a rod would be a function of the position along the length of the rod. A one-millimeter segment of the rod at one position would have a different mass than that of a one-millimeter segment of the rod at a different position.
People with some exposure to calculus have an easier time understanding what linear density is than calculus-deprived individuals do because linear density is just the ratio of the amount of mass in a rod segment to the length of the segment, in the limit as the length of the segment goes to zero. Consider a rod that extends from 0 to L along the x axis. Now suppose that ms(x) is the mass of that segment of the rod extending from 0 to x where x≥0 but x<L. Then, the linear density of the rod at any point x along the rod, is just dmsdx evaluated at the value of x in question.
Now that you have a good idea of what we mean by linear mass density, we are going to illustrate how one determines the position of the center of mass of a non-uniform thin rod by means of an example.
Find the position of the center of mass of a thin rod that extends from 0 to .890m along the x axis of a Cartesian coordinate system and has a linear density given by μ(x)=0.650kgm3x2. Solution
In order to be able to determine the position of the center of mass of a rod with a given length and a given linear density as a function of position, you first need to be able to find the mass of such a rod. To do that, one might be tempted to use a method that works only for the special case of a uniform rod, namely, to try using m=μL with L being the length of the rod. The problem with this is, that μ varies along the entire length of the rod. What value would one use for μ? One might be tempted to evaluate the given μ at x=L and use that, but that would be acting as if the linear density were constant at μ=μ(L). It is not. In fact, in the case at hand, μ(L) is the maximum linear density of the rod, it only has that value at one point on the rod.
What we can do is to say that the infinitesimal amount of mass dm in a segment dx of the rod is μdx. Here we are saying that at some position x on the rod, the amount of mass in the infinitesimal length dx of the rod is the value of μ at that x value, times the infinitesimal length dx. Here we don’t have to worry about the fact that μ changes with position since the segment dx is infinitesimally long, meaning, essentially, that it has zero length, so the whole segment is essentially at one position x and hence the value of μ at that x is good for the whole segment dx.
\boldsymbol{dm=\mu (x) dx \label{22-2}}
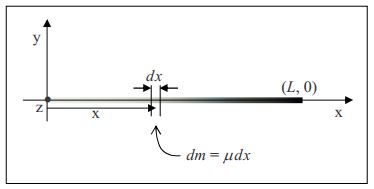
Now this is true for any value of x, but it just covers an infinitesimal segment of the rod at x. To get the mass of the whole rod, we need to add up all such contributions to the mass. Of course, since each dm corresponds to an infinitesimal length of the rod, we will have an infinite number of terms in the sum of all the dm’s. An infinite sum of infinitesimal terms, is an integral.
\boldsymbol{\int dm=\int_{0}{L} \mu (x) dx \label{22-3}}
where the values of x have to run from 0 to L to cover the length of the rod, hence the limits on the right. Now the mathematicians have provided us with a rich set of algorithms for evaluating integrals, and indeed we will have to reach into that toolbox to evaluate the integral on the right, but to evaluate the integral on the left, we cannot, should not, and will not turn to such an algorithm. Instead, we use common sense and our conceptual understanding of what the integral on the left means. In the context of the problem at hand, ∫dm means “the sum of all the infinitesimal bits of mass making up the rod.” Now, if you add up all the infinitesimal bits of mass making up the rod, you get the mass of the rod. So ∫dm is just the mass of the rod, which we will call m. Equation 22A.2 then becomes
\boldsymbol{m=\int_{0}{L} \mu(x) dx \label{22-4}}
Replacing μ(x) with the given expression for the linear density μ=0.650kgm3x2 which I choose to write as μ=bx2 with b being defined by b=0.650kgm3 we obtain
m=∫0Lbx2dx
Factoring out the constant yields
m=b∫0Lx2dx
When integrating the variable of integration raised to a power all we have to do is increase the power by one and divide by the new power. This gives
m=bx33|L0
Evaluating this at the lower and upper limits yields
m=b(L33−033)
m=bL33
The value of L is given as 0.890m and we defined b to be the constant 0.650kgm3 in the given expression for μ, μ=0.650kgm3x2, so
m=0.650kgm3(0.890m)33
m=0.1527kg
That’s a value that will come in handy when we calculate the position of the center of mass. Now, when we calculated the center of mass of a set of discrete particles (where a discrete particle is one that is by itself, as opposed, for instance, to being part of a rigid body) we just carried out a weighted sum in which each term was the position of a particle times its weighting factor and the weighting factor was that fraction, of the total mass, represented by the mass of the particle. We carry out a similar procedure for a continuous distribution of mass such as that which makes up the rod in question. Let’s start by writing one single term of the sum. We’ll consider an infinitesimal length dx of the rod at a position x along the length of the rod. The position, as just stated, is x, and the weighting factor is that fraction of the total mass m of the rod that the mass dm of the infinitesimal length dx represents. That means the weighting factor is dmm, so, a term in our weighted sum of positions looks like:
dmmx
Now, dm can be expressed as μdx so our expression for the term in the weighted sum can be written as
μdxmx
That’s one term in the weighted sum of positions, the sum that yields the position of the center of mass. The thing is, because the value of x is unspecified, that one term is good for any infinitesimal segment of the bar. Every term in the sum looks just like that one. So we have an expression for every term in the sum. Of course, because the expression is for an infinitesimal length dx of the rod, there will be an infinite number of terms in the sum. So, again we have an infinite sum of infinitesimal terms. That is, again we have an integral. Our expression for the position of the center of mass is:
ˉx=∫0Lμdxmx
Substituting the given expression μ(x)=0.650kgm3x2 for μ, which we again write as μ=bx2 with b being defined by b=0.650kgm3, yields
ˉx=∫0Lbx2dxmx
Rearranging and factoring the constants out gives
ˉx=bm∫0Lx3dx
Next we carry out the integration
ˉx=bmx44|L0
ˉx=bm(L44−044)
ˉx=bL44m
Now we substitute values with units; the mass m of the rod that we found earlier, the constant b that we defined to simplify the appearance of the linear density function, and the given length L of the rod:
ˉx=(0.650kgm3)(0.890m)44(0.1527kg)
ˉx=0.668m
This is our final answer for the position of the center of mass. Note that it is closer to the denser end of the rod, as we would expect. The reader may also be interested to note that had we substituted the expression m=bL33 that we derived for the mass, rather than the value we obtained when we evaluated that expression, our expression for ˉx would have simplified to 34L which evaluates to ˉx=0.668m, the same result as the one above.
Moment of Inertia—a.k.a. Rotational Inertia
You already know that the moment of inertia of a rigid object, with respect to a specified axis of rotation, depends on the mass of that object, and how that mass is distributed relative to the axis of rotation. In fact, you know that if the mass is packed in close to the axis of rotation, the object will have a smaller moment of inertia than it would if the same mass was more spread out relative to the axis of rotation. Let’s quantify these ideas. (Quantify, in this context, means to put into equation form.)
We start by constructing, in our minds, an idealized object for which the mass is all concentrated at a single location which is not on the axis of rotation: Imagine a massless disk rotating with angular velocity w about an axis through the center of the disk and perpendicular to its faces. Let there be a particle of mass m embedded in the disk at a distance r from the axis of rotation. Here’s what it looks like from a viewpoint on the axis of rotation, some distance away from the disk:
where the axis of rotation is marked with an O. Because the disk is massless, we call the moment of inertia of the construction, the moment of inertia of a particle, with respect to rotation about an axis from which the particle is a distance r.
Knowing that the velocity of the particle can be expressed as v=rω you can show yourself how I must be defined in order for the kinetic energy expression K=12Iω2 for the object, viewed as a spinning rigid body, to be the same as the kinetic energy expression K=12mv2 for the particle moving through space in a circle. Either point of view is valid so both viewpoints must yield the same kinetic energy. Please go ahead and derive what I must be and then come back and read the derivation below.
Here is the derivation:
Given that K=12mv2, we replace v with rω.
This gives K=12m(rω)2
which can be written as
K=12(mr2)ω2
For this to be equivalent to
K=12Iω2
we must have
I=mr2
This is our result for the moment of inertia of a particle of mass m, with respect to an axis of rotation from which the particle is a distance r.
Now suppose we have two particles embedded in our massless disk, one of mass m1 at a distance r1 from the axis of rotation and another of mass m2 at a distance r2 from the axis of rotation.
The moment of inertia of the first one by itself would be
I1=m1r21
and the moment of inertia of the second particle by itself would be
I2=m2r22
The total moment of inertia of the two particles embedded in the massless disk is simply the sum of the two individual moments of inertial.
I=I1+I2
I=m1r21+m2r22
This concept can be extended to include any number of particles. For each additional particle, one simply includes another mir2i term in the sum where mi is the mass of the additional particle and ri is the distance that the additional particle is from the axis of rotation. In the case of a rigid object, we subdivide the object up into an infinite set of infinitesimal mass elements dm. Each mass element contributes an amount of moment of inertia
\boldsymbol{dI=r^2dm \label{22-6}}
to the moment of inertia of the object, where r is the distance that the particular mass element is from the axis of rotation.
Find the moment of inertia of the rod in Example ??? with respect to rotation about the z axis. Solution
In Example ???, the linear density of the rod was given as μ=0.650kgm3x2. To reduce the number of times we have to write the value in that expression, we will write it as μ=bx2 with b being defined as b=0.650kgm3.
The total moment of inertia of the rod is the infinite sum of the infinitesimal contributions
\boldsymbol{dI=r^2 dm \label{22-6}}
from each and every mass element dm making up the rod.
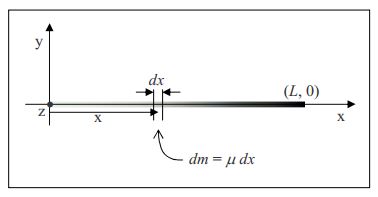
In the diagram, we have indicated an infinitesimal element dx of the rod at an arbitrary position on the rod. The z axis, the axis of rotation, looks like a dot in the diagram and the distance r in dI=r2dm, the distance that the bit of mass under consideration is from the axis of rotation, is simply the abscissa x of the position of the mass element. Hence, equation 22A.4 for the case at hand can be written as
dI=x2dm
which we copy here
dI=x2dm
By definition of the linear mass density μ, the infinitesimal mass dm can be expressed as dm=μdx. Substituting this into our expression for dI yields
dI=x2μdx
Now μ was given as bx2 (with b actually being the symbol that I chose to use to represent the given constant 0.650kgm3). Substituting bx2 in for μ in our expression for dI yields
dI=x2(bx2)dx
dI=bx4dx
This expression for the contribution of an element dx of the rod to the total moment of inertia of the rod is good for every element dx of the rod. The infinite sum of all such infinitesimal contributions is thus the integral
∫dI=∫0Lbx4dx
Again, as with our last integration, on the left, we have not bothered with limits of integration— the infinite sum of all the infinitesimal contributions to the moment of inertia is simply the total moment of inertia.
I=∫0Lbx4dx
On the right we use the limits of integration 0 to L to include every element of the rod which extends from x=0 to x=L, with L given as 0.890m. Factoring out the constant b gives us
I=b∫0Lx4dx
Now we carry out the integration:
I=bx55|L0
I=b(L55−055)
I=bL55
Substituting the given values of b and L yields:
I=0.650kgm3(0.890m)55
I=0.0726kg⋅m2
The Parallel Axis Theorem
We state, without proof , the parallel axis theorem:
I=Icm+md2
in which:
- I is the moment of inertia of an object with respect to an axis from which the center of mass of the object is a distance d.
- Icm is the moment of inertia of the object with respect to an axis that is parallel to the first axis and passes through the center of mass.
- m is the mass of the object
- d is the distance between the two axes.
The parallel axis theorem relates the moment of inertia ICM of an object, with respect to an axis through the center of mass of the object, to the moment of inertia I of the same object, with respect to an axis that is parallel to the axis through the center of mass and is at a distance d from the axis through the center of mass.
A conceptual statement made by the parallel axis theorem is one that you probably could have arrived at by means of common sense, namely that the moment of inertia of an object with respect to an axis through the center of mass is smaller than the moment of inertia about any axis parallel to that one. As you know, the closer the mass is “packed” to the axis of rotation, the smaller the moment of inertia; and; for a given object, per definition of the center of mass, the mass is packed most closely to the axis of rotation when the axis of rotation passes through the center of mass.


