3.4: Relative Motion
- Page ID
- 19375
In order to describe the motion of an object confined to a straight line, we introduced a an axis (\(x\)) with a specified direction (in which \(x\) increases) and an origin (where \(x=0\)). Sometimes, it can be more convenient to use an axis that is moving. For example, consider a person, Alice, moving inside of a train headed for the French town of Nice. The train is moving with a constant speed, \(v^{'B}\) as measured from the ground. Suppose that another person, Brice, describes Alice’s position using the function \(x^{A}(t)\) using an \(x\)-axis defined inside of the train car (\(x=0\) where Brice is sitting, and positive \(x\) is in the direction of the train’s motion), as depicted in Figure \(\PageIndex{1}\) below. As long as any person is in the train with Brice, they will easily be able to describe Alice’s motion using the x-axis that is moving with the train. Suppose that the train goes through the French town of Hossegor, where a surfer, Igor, watches the train go by. If Igor wishes to describe Alice’s motion, it is easier for him to use a different axis, say \(x^{'}\), that is fixed to the ground and not moving with the train.
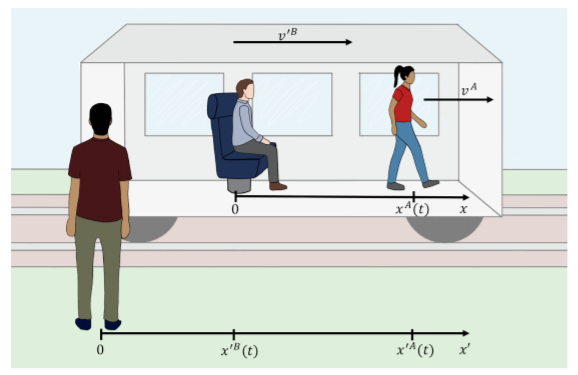
Since Brice already went through the work of determining the function \(x^{A}(t)\) in the reference frame of the train, we wish to determine how to transform \(x^{A}(t)\) into the reference frame of the train station, \(x^{'A}(t)\), so that Igor can also describe Alice’s motion. In other words, we wish to describe Alice’s motion in two different reference frames.
A reference frame is simply a choice of coordinates, in this case, a choice of x-axis. Ideally, in physics, we prefer to use inertial reference frames, which are reference frames that are either “at rest” or that are moving at a constant speed relative to a frame that we consider at rest.
In principle, if you blocked out all of the windows in the train, it would not be possible for Alice and Brice to determine if the train is moving at constant speed or if it is stopped. Thus, the concept of a “rest frame” is itself arbitrary. It is not possible to define a frame of reference that is truly at rest. Even Igor’s frame of reference, the train station, is on the planet Earth, which is moving around the Sun with a speed of \(108000\text{km/h}\).
Galilean Relativity
Not only is it impossible to define a frame of reference that is truly at rest, the rules from transforming from one frame to the other depend on the speed between the reference frames. Our common experience is described by what we call “Galilean Relativity”, but if the speed between trains is very large, close to the speed of light, then we need to use Einstein’s Special Theory of Relativity.
Referring to Figure \(\PageIndex{1}\), we wish to use Brice’s description of Alice’s motion, \(x^{A}(t)\), and convert it into a description, \(x^{'A}(t)\), that Igor can use in the train station. Since Brice is at rest in the train, the speed of Brice relative to Igor is \(v^{'B}(t)\) (the speed of the train, or the speed of the \(x\) frame of reference relative to the \(x^{'}\) frame of reference). The first step is for Igor to describe Brice’s position, \(x^{'B}(t)\), (that is, the position of Brice’s origin).
Assume that we choose \(t = 0\) to be the point in time where the two origins are aligned. Since the train is moving at a constant speed, \(v^{'B}\) (as measured by Igor), then the position of Brice’s origin, \(x^{'B}(t)\), as measured from Igor’s origin is given by:
\(x^{'B}(t)=v^{'B}t\)
Now that Igor can describe the position of the origin of Brice’s coordinate system, he can use Brice’s description of Alice’s motion. Recall that \(x^A(t)\) is Brice’s measure of Alice’s distance from his origin. Similarly, \(x'^B(t)\), is Igor’s measure of the distance from his origin to Brice’s origin. Thus, to obtain Alice’s distance from Igor’s origin, we simply add the distance, \(x'^B(t)\), from Igor’s origin to Brice’s origin, and then add, \(x^A(t)\), the distance from Brice’s origin to Alice. Thus:
\[x'^A(t)=x'^B(t)+x^A(t)=v'^Bt+x^A(t)\]
which tells us how to obtain the position of object \(A\) in the \(x^{'}\) reference frame, when \(x^{A}(t)\) is the description the object’s position in the \(x\) reference frame which is moving with a velocity \(v^{'B}\) relative to the \(x^{'}\) reference frame.
Since we know the position of Alice as measured in Igor’s frame of reference, we can now easily find her velocity and her acceleration, as measured by Igor. Her velocity as measured by Igor, \(v^{'A}\), is given by the time-derivative of her position measured in Igor’s frame of reference:
\[\begin{aligned} v^{'A}(t)&=\frac{d}{dt}x^{'A}(t)\\[4pt] &=\frac{d}{dt}(v^{'B}t+x^{A}(t))\\[4pt] &=v^{'B}+\frac{d}{dt}x^{A}(t)\\[4pt] &=v^{'B}+v^{A}(t)\end{aligned}\]
where \(v^A(t)=\frac{d}{dt}x^A(t)\) is Alice’s speed as measured by Brice, in the train. That is, the velocity of Alice as measured by Igor is the sum of the velocity of the train relative to the ground and the velocity of Alice relative to the train, which makes sense. If we now determine Alice’s acceleration, \(a'^A(t)\), as measured by Igor, we find:
\[a^{'A}(t)=\frac{d}{dt}v^{'A}(t)\]
\[=\frac{d}{dt}(v^{'B}+v^{A})\]
\[=0+\frac{d}{dt}v^A(t)\]
\[=a^A\]
where we have explicitly used the fact that the train is moving at constant velocity (\(\frac{d}{dt}v^{'B}=0\)). Here we find that both Brice and Igor will measure the same number when referring to Alice’s acceleration (if the train is moving at constant velocity). This is a particularity of “inertial” frame of references: accelerations do not depend on the reference frame, as long as the reference frames are moving with a constant velocity relative to each other. As we will see later, forces exerted on a object are directly related to the acceleration experienced by that object. Thus, the forces on a object do not depend on the choice of inertial reference frame.
A large boat is sailing North at a speed of \(v^{'B}=15\text{m/s}\) and a restless passenger is walking about on the deck. Chloë, another passenger on the boat, finds that the passenger is walking at a constant speed of \(v^{A}=3\text{m/s}\) towards the South (opposite the direction of the boat’s motion). Marcel is watching the boat pass by from shore. What velocity (magnitude and direction) does Marcel measure for the restless passenger?
Solution
First, we must choose coordinate systems in the boat and on the shore. On the boat, let us define an \(x\) axis that is positive in the North direction and has an origin such that the position of the restless passenger was \(x^{A}(t=0)=0\) at time \(t=0\). In Chloë’s reference frame, the passenger is thus described by:
\[x^{A}(t)=v^{A}t=(-3\text{m/s})t\]
where we note that \(v^{A}\) is negative since the passenger is moving the in negative \(x\) direction (the passenger is walking towards the South, but we chose positive \(x\) to be in the North direction). On shore, we choose an \(x^{'}\) axis that also is positive in the North direction. We can choose the origin such that the origin of the boat’s coordinate system was \(x^{'}=0\). The origin of the boat’s coordinate system as measured by Marcel (on shore) is thus:
\[x^{'B}(t)=v^{'B}t=(15\text{m/s})t\]
The position of the passenger, \(x^{'A}(t)\), as measured by Marcel, is then given by adding the position of the boat’s origin and the position of the passenger as measured from the boat’s origin:
\[\begin{aligned} x^{'A}(t) &= x^{'B}(t)+x^{A}(t)\\[4pt] &= v^{'B}t + v^{A}t \\[4pt] &= (v^{'B}+v^{A})t\\[4pt] &= ((15\text{m/s})+(-3\text{m/s}))t\\[4pt] &= (12\text{m/s})t\end{aligned}\]
To find the velocity of the passenger as measured by Marcel, we take the time derivative:
\[\begin{aligned} v^{'A} &= \frac{d}{dt}x^{'A}(t)\\[4pt] &= \frac{d}{dt} \left((v^{'B}+v^{A})t\right)\\[4pt] &=(v^{'B}+v^{A})\\[4pt] &=((15\text{m/s})+(-3\text{m/s}))\\[4pt] &=12\text{m/s}\end{aligned}\]
Since this is a positive number, Marcel still sees the passenger moving in the North direction (the direction of his positive \(x'\) axis), but with a speed of \(12\) m/s, which is less than that of the boat. On the boat, the passenger appears to be walking towards the South, but the net motion of the passenger relative to the ground is still in the North direction, as their speed is less than that of the boat.