4.7: Sample problems and solutions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Ethan is jumping hurdles. He gets a running start, moving with a speed of 3m/s. The hurdle is 0.5m high and the maximum speed that he can have when he leaves the ground is 5m/s. (You can assume Ethan is a point particle, and ignore air resistance).
- What is the closest distance from the hurdle at which Ethan can jump and still clear the hurdle?
- What maximum height does he reach?
- Answer
-
Our approach will be to consider the x and y components of the motion separately. We start by drawing a diagram and choosing our coordinate system. We will choose y to be vertical and positive upwards and x to be in the direction that Ethan is running. We choose the origin to be the location where Ethan leaves the ground for the jump, as illustrated in Figure 4.7.1.
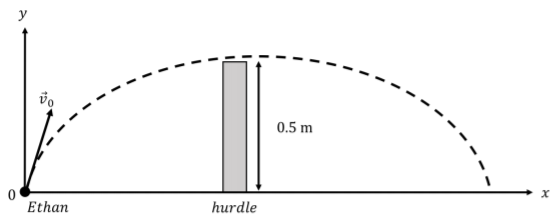
Figure 4.7.1: Ethan wants to clear a 0.5 m hurdle and has an initial velocity →v0 with x and y components. a. Ethan’s speed at the beginning of the jump is v0=5m/s and the horizontal (x) component of his velocity is vx=3m/s. The y component of his initial velocity, v0y, is given by:
v2x+v20y=v20v0y=√v20−v2xv0y=√(5m/s)2−(3m/s)2=4m/s
We chose the origin at the beginning of the jump, so that Ethan’s x and y coordinates at time t=0 are x0=0 and y0=0, respectively. Once Ethan is in the air, there will be no acceleration in the x direction, and the only acceleration is in the y direction and will be that due to gravity. Ethan’s position at any time t can be described by the following equations:
x(t)=vxty(t)=v0yt−12gt2
where g is the acceleration due to gravity, g=9.8m/s^2.
We want to determine the value of x(t) when the vertical displacement, y(t), is equal to the height of the hurdle, h. We thus find the value of t when y=0.5m and then find the value of x at that time.
We can re-arrange the equation for y(t) and solve the resulting quadratic for t (we get two solutions):
0=−12gt2+v0yt−h0=12(−9.8m/s2)t2+(4m/s)t−0.5mt=0.15s,0.66s
The jump will be a parabola, and Ethan will cross a height of 0.5m twice, once on the way up, and once on the way down. We want to know when Ethan reaches 0.5m for the first time (on the way up), so we choose t=0.15s. The horizontal displacement at this time is:
x=vxt=(3m/s)(0.15s)=0.45m
Therefore, he can get as close as 0.45m from the hurdle before he has to jump, if his initial horizontal velocity is 3m/s.
b. Ethan’s motion follows a parabolic shape. At the maximum height, Ethan’s vertical velocity is equal to zero. We can model only the vertical part of the motion to solve for the value of y when vy=0. We know the following quantities:
v0y=4m/svy=04.7.m/sg=9.8m/s2
The easiest way to determine y is to use the formula,
v2y=v20y−2g(y−y0)∴y=v2y−v20y(−2g)
Substituting our values for vy, v0y, and g, we get:
ymax=(−4m/s)2(2)(−9.8m/s2)ymax=0.82m
Ethan reaches a maximum height of 0.82m.
A cowboy swings a lasso above his head. The lasso moves at a constant speed in a circle of radius 1.5m in the horizontal plane. A hawk flies toward the lasso at 50km/h. The hawk sees the end of the lasso moving at 60km/h when the lasso is directly in front of it (see Figure 4.7.2). In the reference frame of the cowboy ...
- How long does it take for the lasso to complete one revolution? (Hint: From the point of view of the hawk, the lasso is moving towards him in addition to moving in a circle. You will have to use your knowledge of relative motion to solve this problem!)
- What is the centripetal acceleration of the end of the lasso?
- What is the angular acceleration of the lasso?
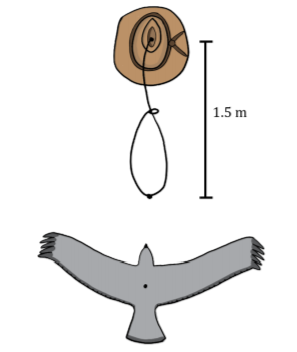
- Answer
-
a. We need to determine the speed of the end of the lasso in the cowboy’s frame of reference, knowing its speed in the hawk’s frame of reference and knowing the velocity of the hawk. Once we know the speed of the lasso in the cowboy’s frame of reference we can easily determine how long it takes to complete one revolution (its period).
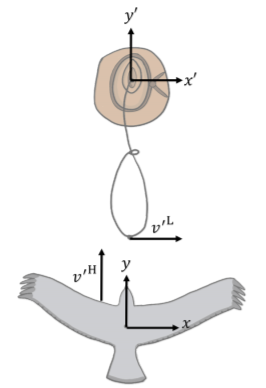
Figure 4.7.3: The two coordinate systems are aligned so that positive y′ and positive y are in the same direction. The velocity vectors of the hawk and the lasso in the reference frame of the cowboy are shown. We start by introducing coordinate systems for the hawk (xy) and the cowboy (x′y′), and choose for the x (y) and x′ (y′) axes to be parallel. We choose the axes such that x is to the right (when seen from above, as in Figure 4.7.3) and y is in the direction of motion of the hawk as seen in the cowboy’s reference frame. The velocity vector of the hawk in the cowboy’s frame of reference is:
→v′H=v′Hˆy=(50km/h)ˆy
In the hawk’s frame of reference, the lasso will have a y component of velocity in the negative y direction with the same magnitude as the speed of the hawk, and an unknown component, vLx, in the x direction. The velocity of the lasso in the hawk’s frame of reference is:
→vL=vLxˆx−v′Hˆy
However, we know the speed of the lasso in the hawk’s frame of reference (vL=60km/h), so we can easily find vLx:
vLx=√v2L−v′2H=√(60km/h)2−(50km/h)2=33.17km/h
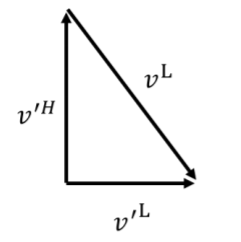
Figure 4.7.4: Vector addition to determine the velocity of the lasso in the cowboy’s reference frame. In the cowboy’s frame of reference, the lasso will have a velocity vector (Figure 4.7.4), →v′L, given by:
→v′L=→v′H+→vL=v′Hˆy+vLxˆx−v′Hˆy=vLxˆx=(33.17km/h)ˆx
That is, in the cowboy’s frame of reference, the lasso has a velocity that is in the x direction. This corresponds to the speed, vs, of the end of the lasso in uniform circular motion about a circle of radius R=1.5m. We can thus find the time required for one revolution to be:
vs=2πRT∴T=2πRvs=2π(1.5m)(33.17km/h)=2π(1.5m)(9.2m/s)=1.02s
where we converted the speed into m/s before determining the time.
b. The motion is uniform circular motion, so it has a centripetal acceleration given by
ac(t)=v2s(t)R
To find the centripetal acceleration of the end of the lasso, we just user our values for vs and R.
ac(t)=(9.2m/s)21.5m=56m/s2
c. The angular acceleration of the lasso is zero. The angular acceleration refers to the rate of change of the angular velocity (the rate at which the lasso rotates), which is constant for uniform circular motion.

