5.2: Force
( \newcommand{\kernel}{\mathrm{null}\,}\)
A force is a mathematical tool that is introduced in Newton’s theory of physics. A force is not a real “thing”; there are no forces in the real world, you cannot give someone a force, or buy a force at the supermarket. A force is a purely mathematical tool, so it is important to fight your intuition about what a force is and to stick to well-defined rules for identifying forces to build models.
Mathematically, a force is represented by a vector, and thus has a magnitude and a direction. The SI unit for the magnitude of a force is the “Newton”, abbreviated, N. A force is used to describe how the motion of an object is affected by external agents. It is important to note that a force can be exerted by an inanimate being; that is, there is no intent - no conscious decision to push or pull - associated with a force.
When you push a block along a horizontal surface, we would model the motion of the block as being related to a force that you exert on the block in the direction that you are pushing and with a magnitude that is proportional to how hard you are pushing. Newton’s Third Law states that the block will exert a force on you that is of equal magnitude but in the opposite direction; if we want to model your motion, we will need to include that force exerted by the block on you.
If you are pulling on a cart, we would model the motion of the cart by including a force that is exerted on the cart by you. The force would be represented by a vector in the direction that you are pulling with a magnitude based on how hard you are pulling. Similarly, to model your motion, we would include a force vector that is equal in magnitude and opposite in direction to represent the force exerted by the cart on you. When modeling the motion of an object, it is important to consider only the forces exerted on that object.
One way to quantify a force is to use a spring scale. Springs have a natural “rest length” if not acted upon by external forces. If you try to stretch a spring, it will “want” to come back to its normal rest length; it exerts a force on your hand in the opposite direction from the one you are pulling on the spring. You may have noticed that the more you stretch a spring, the harder you have to pull on it. We can quantify the magnitude of a force by the distance that the forces causes a spring to stretch, since that distance increases with what we conceptualize as a force. For example, one could designate a “standard spring” to be one that extends (or compresses) by 1cm when a force of 1N is exerted on the spring in the direction co-linear with the axis of the spring. We could then use that “standard spring” to measure the magnitude of any force.
Types of forces
When modeling the dynamics of an object, we need to identify all of the forces exerted on that object. Some of the forces can be classified as “contact forces” as they arise from something making contact with the object (such as you pushing on the object). Other forces can be exerted “at a distance”; for example, the force of gravity from the Earth can be exerted on a bird in flight, even if the bird is not in contact with the Earth. In reality, contact forces arise because the electrons from two objects repel each other. When you push against a wall, the reason that you feel a resistance is because the electrons on your hand are repelled by the electrons on the wall; you never actually “touch” the wall1!
In this section, we list and describe the most common types of forces that arise when modeling the motion of an object. When determining the forces that are acting on an object, it is usually a good idea to run down this list to see if any of these forces should be included. Again, try to fight your intuition about what a force “feels” like and instead be objective in determining whether any of the forces below should be included based on their characteristics.
Weight
Weight is the force exerted by gravity. While all objects with mass exert an attractive force of gravity on all other objects with mass, that force is usually negligible unless the mass of one of the objects is very large. For an object near the surface of the Earth, we can, to a very good degree of approximation, assume that the only force of gravity on the object is from the Earth. We usually label the force of gravity on an object as →Fg. All objects near the surface of the Earth will experience a weight, as long as they have a mass. If an object has a mass, m, and is located near the surface of the Earth, it will experience a force (its weight) that is given by:
→Fg=m→g
where →g is the Earth’s “gravitational field” vector and points towards the center of the Earth. Near the surface of the Earth, the magnitude of the gravitational field is approximately g=9.8N/kg. The gravitational field is a measure of the strength of the force of gravity from the Earth (it is the gravitational force per unit mass). The magnitude of the gravitational field is weaker as you move further from the center of the Earth (e.g. at the top of a mountain, or in Earth’s orbit). The gravitational field is also different on different planets; for example, at the surface of the moon, it is approximately gm=1.62N/kg (six times less) - thus the weight of an object is six times less at the surface of the moon (but its mass is still the same). As we will see, the magnitude of the gravitational field from any spherical body of mass M (e.g a planet) is given by:
g(r)=GMr2
where G=6.67×10−11 is Newton’s constant of gravity, and r is the distance from the center of the object.
Although we have not yet introduced the concept of mass, it is worth emphasizing that mass and weight are different (they have different dimensions). Mass is an intrinsic property of an object, whereas weight is a force of gravity that is exerted on that object because it has mass and is located next to another object with mass (e.g. the Earth). On Earth, when we measure our weight, we usually do so by standing on a spring scale, which is designed to measure a force by compressing a spring. We are thus measuring mg, which can easily be related to our mass since, on Earth, weight and mass are related by a factor of g=9.8N/kg; this is usually what leads to the confusion between mass and weight.
A person standing on a scale finds that they weigh 80kg.
- They exert an upwards force on the Earth with a magnitude of 80N.
- They exert an upwards force on the Earth with a magnitude of 784N.
- They exert an downwards force on the Earth with a magnitude of 80N.
- They exert an downwards force on the Earth with a magnitude of 784N.
- They exert no force on the Earth.
- Answer
- B.
Normal forces
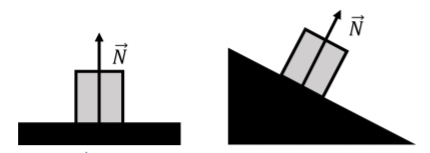
Normal forces are exerted when two surfaces are in contact and “pushing” against each other. For example, if a block is resting on a horizontal table, the table will exert a normal force on the block that is upwards. The force is called “normal” because it is normal (i.e. perpendicular) to the interface between the two objects. The normal force exerted by a surface onto an object points in the direction from the surface to the object in such a way that it is perpendicular to the interface between the surface and the object. Because of Newton’s Third Law, whenever an object experiences a normal force from a surface, the object also exerts a force of the same magnitude (in the opposite direction) on the surface. The magnitude of the normal force exerted by a surface onto an object, in general, depends on the other forces that are exerted on the object. For example, if a block is on a table, it will experience a stronger normal force if you exert a downwards force on the block.
Figure 5.2.2 shows two examples of the normal force on a block that is exerted by a surface (it is explicitly assumed that the block also experiences a downwards force from gravity that is not shown). In both cases, the normal force, →N, is perpendicular to the interface and in the direction that goes from the interface towards the object.
Frictional forces
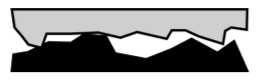
A frictional force can exist at the interface between two surfaces and is always perpendicular to the normal force that corresponds to that interface. A frictional force is used to model the resistance that is felt when one tries to slide an object along a surface. The frictional force is used to model the details of how two surfaces interact at a microscopic level; since surfaces are never perfectly flat, two surfaces will never slide without resistance as the various bumps and valleys of the two surfaces will interact (Figure 5.2.3). Furthermore, even if the two surfaces were perfectly smooth, the electrons on the two surfaces would still interact and lead to an effective force when one surface moves with respect to the other.
One distinguishes between two types of frictional forces: kinetic and static, depending on whether the surfaces are sliding with respect to each other (kinetic) or not (static). Because of Newton’s Third Law, the objects associated with each surface will both experience a frictional force (same magnitude, opposite direction).
The frictional force exerted on an object is always parallel to the surface of the object. For the kinetic force of friction, the force is exerted in the direction that is opposite to the motion of the object relative to the surface. For the static force of friction, the force is exerted in the direction that is opposite to the impeding motion. If a block is sliding towards the right on a table (Figure 5.2.4, left), it will experience a kinetic force of friction that is to the left. The table will then experience a force of friction that is to the right (Newton’s Third Law). If there is a heavy crate on the ground which you try to push but does not move (Figure 5.2.4, right), there is a force of static friction exerted by the ground on the object that is in the opposite direction that you are pushing.
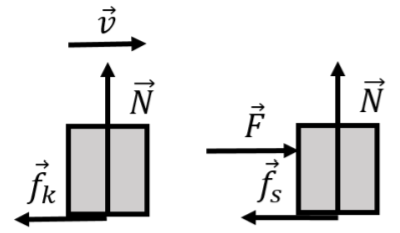
One key difference between the forces of static and kinetic friction is that the magnitude of the force of static friction can vary in magnitude; the force of static friction on the crate increases as you push harder, until you push hard enough to overcome the maximal force of static friction that can exist between the ground and the crate. Often, the force of kinetic friction is smaller than the static force of friction; you may have noticed that you have to push very hard to get an object sliding, but once it is sliding, you do not need to push as hard to keep it moving.
The magnitude of the kinetic force of friction between two surfaces, fk, is modeled as being proportional to the normal force between the two surfaces:
fk=μkN
where μk is called the “coefficient of kinetic friction” and depends on the two surfaces. If you push down on an object, it is more difficult to slide it along a surface, because the normal force, and thus the kinetic friction force increases.
Similarly, the maximum magnitude of the force of static friction between to surfaces, fs, is modeled as:
fs≤μsN
where μs is called the “coefficient of static friction” and the inequality sign is used to indicate that the force of static friction has a maximum value, but that its magnitude depends on the other forces being exerted on the object. For example, if you do not push against a crate on a horizontal surface, there is no force of static friction on the crate (as long as no other forces are exerted that are parallel to the surface).
Tension forces
Tension forces are “pulling” forces that are applied by a rope or other non rigid media (e.g. a chain) which cannot usually be used to push2. If you attach a rope to a crate and use the rope to pull the crate, we call the force exerted by the rope onto the crate a force of tension.
When you pull on a rope that is attached to a wall at the other end, we say that the rope is under tension, or that the tension force is present throughout the rope. If you pull really hard on the rope, it is harder to displace the center of the rope (or any other point) than if you did not pull on the rope at all. It thus makes sense to view the tension as being present throughout the rope. The force of tension that a rope can apply onto an object depends on what is pulling on the rope at the other end. A rope can be used to change the direction of a force, as illustrated in Figure 5.2.5, which shows a pulley and rope being used to lift a block vertically by applying a horizontal force, →F, to the rope.
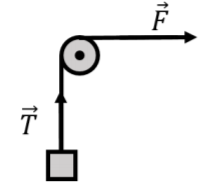
The same tension is present throughout sections of the rope that can move freely. Imagine a rope lying on the ground and someone pressing down with their foot on the rope at its midpoint. If you pull on one end of the rope with your hand, there will be a tension in the section of the rope between your hand and the foot that is pressing on the rope, but the other side of the rope will be slack; the tension is thus different in different sections of the rope. As we will see in later chapters, if a rope goes around a pulley that is accelerating and has mass, then the tension in the rope on either side of the pulley is different; this is similar to the tension being different on either side of the foot pressing down on the rope.
Drag forces
Drag forces are exerted on an object that is moving through a fluid (a gas or a liquid). As an object moves through a fluid, the fluid must be displaced which results in a net force opposing the motion of the object. Drag forces are thus always in the opposite direction of the motion of the object relative to the fluid, similar to friction. Often, one hears the term “air friction” which refers to the drag force experienced by an object that is moving through the air.
There is no good general model for calculating the magnitude of the drag force on any object moving through any fluid. This usually has to be measured; while good software exist for simulating drag, you will still ultimately need to test your new airplane design in a wind tunnel to measure the drag force.
The magnitude of the drag force generally depends on the cross-section of the object (the area of the object as seen when looking at the object in the direction of motion), the speed of the object, and the viscosity of the fluid (how difficult it is to displace the fluid). For small objects moving relatively slowly through a fluid (e.g. pollen falling through the air), the drag force is usually proportional to the object’s speed, whereas for larger objects moving faster through a fluid (e.g a car or airplane moving through the air) the drag force is usually proportional to the speed of the object squared.
Spring forces
Spring forces are those forces that are exerted by those materials and objects that can be compressed or extended. A common example is a simple coil spring, which has a natural rest length. If the spring is extended, the spring will exert “restoring forces” on both ends of the spring that are directed towards the center of the spring. If the spring is compressed, the spring will exert restoring forces that point away from the center of the spring. In either case, the spring will exert forces that would allow it to come back to its rest length.
Most springs, if they are not stretched or compressed too much, will exert a restoring force that is given by Hooke’s Law:
→F=−kxˆx
where →F is the force exerted by the spring, k is called the “spring constant” of the spring, and x is the amount that the spring has been stretched or compressed. The negative sign indicates that the restoring force from the spring will be in the opposite direction that the spring length was changed, and the x axis is defined to be co-linear with the axis of the spring and the origin is located where the spring is at rest. This is illustrated in Figure 5.2.6.
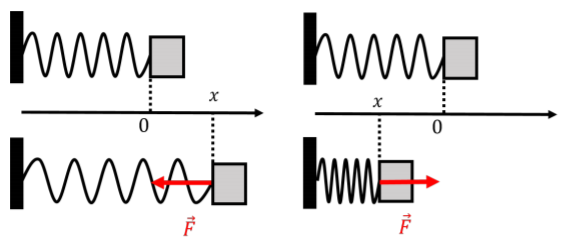
In Figure 5.2.6, we chose the positive x axis to correspond to positions where the spring is extended and verified that Hooke’s Law (→F=−kxˆx) holds. If we had chosen the positive direction to correspond to compression (positive x to the left), would Hooke’s Law still correctly describe the direction of the force exerted by the spring on the block?
- Yes.
- No.
- Answer
- A.
Inertial forces
Inertial forces are exerted on an object when the forces on the object are modeled in a non-inertial frame of reference. For example, in the frame of reference of an accelerating elevator, or that of a car going around a curve, one can use Newton’s Three Laws to model motion, if an additional inertial force is included. In a frame of reference that has an acceleration given by →a, an inertial force −m→a is exerted on an object. This is the nature of the outwards force that is felt when your car goes around a curve, or the perception of being weightless in an elevator that has a large downwards acceleration. We will discuss inertial forces in more detail in Section 5.6.
“Applied” forces
“Applied” forces is just a general “catch-all” term for specifying forces that are not described above. For example, the force applied by a person onto an object is often referred to as an applied force.

