5.6: The acceleration due to gravity
( \newcommand{\kernel}{\mathrm{null}\,}\)
If you have studied some physics before reading this textbook, you may have been surprised by our choice of dimension for g to be force per unit mass rather than acceleration. This is indeed an unconventional choice as g is usually presented as “the acceleration due to Earth’s gravity” instead of the “strength of Earth’s gravitational field”. Our choice comes from the potential difference between inertial mass, mI, and gravitational mass, mG, which we distinguish in this section.
Consider the simple model of a mass falling freely near the surface of the Earth in the absence of air-resistance. The only force exerted on the mass is its weight, mG→g, which is given in terms of gravitational mass (the mass that determines how an object experiences gravity). Both the weight and the acceleration of the object point downwards. The free-body diagram for the mass is shown in Figure 5.6.1, where the y axis was chosen to be vertically upwards (co-linear with the acceleration).
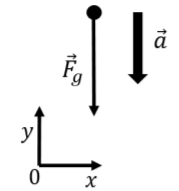
Writing out the y component of Newton’s Second Law, being careful to distinguish between inertial and gravitational mass, and noting that both the weight and the acceleration are in the negative y direction:
∑Fy=−Fg=−mIa∴mGg=mIa
This makes it clear that g is not necessarily the acceleration due to gravity. It is only the acceleration due to gravity in the limit that the inertial and gravitational masses are the same. If mG=mI, then we have:
a=g
and indeed, the acceleration of objects near the surface of the Earth has a magnitude of g. It is also clear that the dimensions of g can also be written as an acceleration, and in most cases, one writes that, near the surface of the Earth, g=9.8m/s2. You should however remember that this is only true when inertial and gravitational masses are the same, and that g really should be thought of as the strength of the gravitational field, not as an acceleration.

