5.7: Non-inertial frames of reference and inertial forces
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the previous sections, we described how to use Newton’s First Law to identify an inertial frame of reference (one where Newton’s First Law holds true) in order to identify the forces exerted on an object so that Newton’s Second Law could be applied. It is possible to apply Newton’s Laws in a non-inertial frame of reference, provided that one includes an additional “inertial force”.
Let us assume that we hang a mass, m, from the ceiling of our car using a string. If the car accelerates forwards with a constant acceleration, →a, the mass will swing towards the back of the car and the string will not be vertical as long as the car maintains its constant acceleration, as shown in Figure 5.7.1. As the car maintains its acceleration, the hanging mass will not move relative to the car.
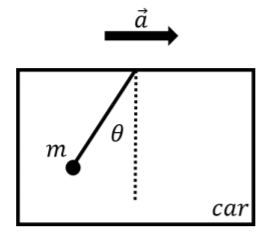
We can analyze this motion from the inertial frame of reference of the ground. In this frame of reference, there are two forces exerted on the mass:
- →Fg, its weight, with magnitude mg.
- →T, a force of tension exerted by the string, in the direction of the string.
The two forces are shown in the free-body diagram of Figure 5.7.2, along with a coordinate system chosen such that x points in the direction of the acceleration the mass (which is the same as the acceleration of the car, since the mass does not move relative to the car).
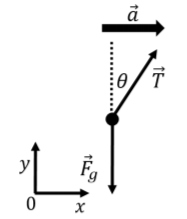
Writing out the x and y components of Newton’s Second Law for the mass, we have:
∑→F=→T+→Fg=m→a∴∑Fx=Tsinθ=ma∴∑Fy=Tcosθ−Fg=0
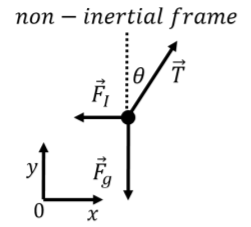
We can, instead, model the motion of the mass in the frame of reference of the car, by pretending that we are sitting in the car. In the frame of reference of the car, the mass is immobile, and thus has no acceleration. In the non-inertial frame of reference of the car, we still have the weight and tension forces exerted on the mass; these have the same magnitude and direction as in the inertial frame of reference of the ground. One could replace the string with a spring scale, and observers in the car and on the ground would agree that the spring scale reads the same number. Those observers would also agree that the weight of the mass is the same. However, the two observers disagree on whether the mass is accelerating, since the observer in the car measures that the mass has no acceleration.
In the frame of reference of the car, the acceleration of the mass is zero. If we want Newton’s Second Law to hold, this implies that, in the reference frame of the car, the sum of the forces on the mass must be zero:
∑→F=0(car reference frame)
We know from analysing the motion from the frame of reference of the ground that the vector sum of the forces →T and →Fg is equal to m→a. The only way for the force in the frame of reference of the car to add up to zero is if there is an additional force, →FI, that is exerted in that frame of reference:
∑→F=→T+→Fg+→FI=0(car reference frame)
Since we know that →T+→Fg=m→a, we can substitute this in the equation above:
∑→F=→T+→Fg+→FI=0(car reference frame)=m→a+→FI=0∴FI=−m→a
and we find that this “inertial force”, →FI, must be exerted in the opposite direction from the acceleration of the frame of reference, with a magnitude given by ma. The free-body diagram for the mass, as viewed in the reference frame of the car, is illustrated in Figure 5.7.3.
You are in an elevator that is accelerating downwards with a constant acceleration →a. You are standing on a spring scale. What is the value of your weight as displayed on the spring scale? Assume that your mass is m. (The spring scale will display your weight as having the same magnitude as the normal force that the scale exerts on you).
Solution
We can model your motion in the non-inertial frame of reference of the elevator, where your acceleration is zero. The forces that are exerted on you are:
- →Fg, your weight, with magnitude mg.
- →N, the normal force exerted upwards by the spring scale, which is the weight as measured by the scale.
- →FI, an inertial force with magnitude ma that is exerted upwards (in the direction opposite of the acceleration of the frame of reference).
The forces in the frame of reference of the elevator are illustrated in Figure 5.6.4, along with a coordinate system that was chosen so that the forces are co-linear with one of the axes (since the acceleration is zero).
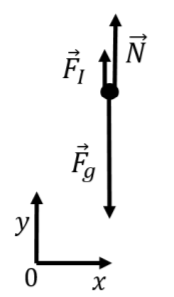
All of the forces are in the vertical direction, so we only need to write out the y component of Newton’s Second Law, which we can easily solve for the normal force:
∑Fy=N+FI−Fg=0N+ma−mg=0∴N=m(g−a)
Remember that you need to be careful about the signs. We have included the fact that FI is exerted upwards with the plus sign in the first equation (the y component of →FI=0ˆx+FIˆy is +FI). We then used the fact that the magnitude of the inertial force is given by FI=ma in the second line.
You can easily verify that you would obtain the same result in the inertial frame of reference of the ground, where there is no inertial force, but the acceleration is non-zero (and in the negative y direction if we use the same coordinate system):
∑Fy=N−mg=−ma(ground frame of reference)
The normal force, which corresponds to weight as read by the scale, is thus N=m(g−a). We should ask ourselves if the result makes sense:
- Since the dimension of a and g are the same, m(g−a) has the correct dimension of force.
- If the acceleration, a, is zero, then the magnitude is N=mg, as it should be if the elevator is at rest with respect to the ground.
- If the acceleration a is equal to g, the normal force exerted by the scale is exactly zero, and your measured weight is zero. This is what we call being “weightless”, which is not a good description, since the force of weight is still applied, and it is the normal force which is zero.
- If the acceleration, a, is bigger than g, then the normal force would be negative. This corresponds to the elevator accelerating downwards faster than gravity, and the model breaks down, since in this case, you would first hit the ceiling of the elevator, which would then exert a downwards normal force with magnitude m(a+g).

