6.4: Non-uniform circular motion
( \newcommand{\kernel}{\mathrm{null}\,}\)
In non-uniform circular motion, an object’s motion is along a circle, but the object’s speed is not constant. In particular, the following will be true
- The object’s velocity vector is always tangent to the circle.
- The speed and angular speed of the object are not constant.
- The angular acceleration of the object is not zero.
- The acceleration vector will not point towards the center of the circle.
Since the acceleration vector does not point towards the center of the circle, it is usually convenient to break up the acceleration vector into two components: aR, a component that is radial (towards the center of the circle), and aT, a component that is tangent to the circle (and perpendicular to to the radial component). The radial component is “responsible” for the change in direction of the velocity such that the object goes in a circle. the magnitude of the radial acceleration is the same as it is for uniform circular motion:
aR=v2r
where the speed is no longer constant in time. The tangential component of the acceleration is responsible for changing the magnitude of the velocity of the object:
aT=dvdt
A small ant is sleeping on a turntable just as the turntable starts to spin from rest, with an angular acceleration α=1rad/s2 that is small enough so that, initially, the ant remains on the turntable. The ant is a distance R=0.1m from the center of the turntable, as shown in Figure 6.4.1 and the coefficient of static friction between the ant’s “feet” and the turntable is μs=0.5. After how much time will the ant slide off from the turntable?
Solution
As the turntable accelerates, the force of static friction between the turntable and the ant will keep the ant moving with the turntable. Once the turntable is going fast enough, the force of friction will no longer be large enough to provide the total acceleration that is required to keep the ant moving with the turntable (with a constant tangential component of the acceleration and an increasing radial component of the acceleration).
The forces on the ant are:
- →Fg, its weight, with magnitude mg.
- →N, a normal force exerted by the turntable on the ant.
- →fs, a force of static friction exerted by the turntable on the ant. The force of friction will be such that it has both radial and tangential components.
A free-body diagram for the forces on the ant is shown in Figure 6.4.2, as seen from above and from the side, for some point in time. We have chosen the point in time to be just when the ant is about to slide off of the turntable, when the force of static friction makes an unknown angle θ with the x axis. We have placed the origin of the coordinate system at the center of the turntable and chosen the x axis such that the ant is located on the positive x axis with its velocity in the positive y direction. We used a three dimensional coordinate system where the weight and normal force are exerted in the z (vertical) direction since the acceleration vector of the ant will have both radial (x) and tangential (y) components.
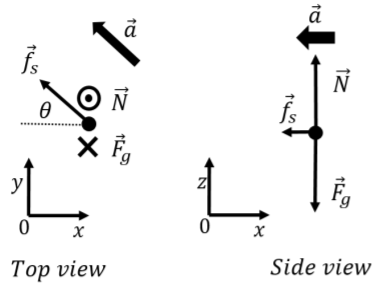
Newton’s Second Law has to be written out in three components. The z component relates the weight and normal force:
∑Fz=N−Fg=0∴N=mg
The x component of Newton’s Second Law is such that the x component of the acceleration is its radial component:
∑Fx=−fscosθ=−maR=−mv2R∴fscosθ=mv2R
The y component of Newton’s Second relates the tangential component of the force of static friction to the tangential component of the acceleration:
∑Fy=fssinθ=maT∴fssinθ=mαR
where we used the fact that the (linear) tangential acceleration, aT, is related to the angular acceleration, α, by:
aT=αR
Summarizing the three equations that we obtained from the three components of Newton’s Second Law:
fscosθ=mv2Rfssinθ=mαRN=mg
Also, note that the speed, v(t) at some time t is given by simple kinematics:
v(t)=v0+aTt=(0)+αRt
The ant will start to slip when the force of friction reaches its maximal amplitude, fs=μsN=μSmg. The x of Newton’s Second Law can be used to find an expression for the time at which force of friction reaches its maximal value (in terms of the unknown angle θ):
fscosθ=mv2Rμsgcosθ=Rα2t2∴t=√μsgcosθRα2
We can use the y component to determine the angle
θ:
fssinθ=mαRμsgsinθ=αR∴sinθ=αRμsg∴θ=sin−1(αRμsg)=sin−1((1rad/s2)(0.1m)(0.5)(9.8N/kg))=1.17⋅
The angle is very small, and we see that the force of friction is mostly directed towards the center of the circle. The radial acceleration is thus much larger than the tangential acceleration. We can then use the angle to find the time using the expression we derived above:
t=√μsgcosθRα2=√(0.5)(9.8N/kg)cos(1.17⋅)(0.1m)(1rad/s2)2=7.0s

