9.4: Einstein’s Theory of General Relativity
( \newcommand{\kernel}{\mathrm{null}\,}\)
Newton’s Universal Theory of Gravity was extremely successful at describing the motion of planets in the solar system, and allowed for high precision astronomy. For example, precision measurements of Uranus’s orbit showed that it appeared to be inconsistent with Newton’s theory, unless the gravitational influence of another planet was included in the model. This led to the discovery of the planet Neptune.
However, some issues with Newton’s theory were uncovered. The orbit of Mercury was shown to be different than what Newton’s theory could describe, but searches for another planet (Vulcan) were unsuccessful. In addition, Albert Einstein’s theory of Special Relativity, published in 1905, was found to be incompatible with Newton’s theory of gravity. One of the consequences of Special Relativity is that nothing can propagate faster than the speed of light. Newton’s Universal Theory of Gravity implies that the gravitational force is transmitted instantaneously. In Newton’s theory, if the Sun suddenly disappeared, Earth would immediately “fall out” of its orbit, and we would immediately know that the Sun has disappeared. This would violate Special Relativity because there cannot be a mechanism that would allow us to know that the Sun has disappeared faster than it would take light to propagate from the Sun. In other words, for the 8 min that are required for light to travel from the Sun to the Earth, we cannot know that the Sun has disappeared: only when we literally see the Sun disappear would the Earth be “allowed” to fall out of its orbit.
Einstein’s Theory of General Relativity is a theory developed by Einstein in order to describe gravity in a way that is consistent with Special Relativity and the propagation of light. Einstein was famous for his “thought experiments,” which allow us to think about some of the implications of a theory, even if the experiments would be very difficult to carry out in practice. One such thought experiment is to consider what someone would observe in an accelerating frame of reference.
Consider an observer in an elevator, as illustrated in Figure 9.4.1. If the elevator is stationary at the surface of the Earth (left panel), and the observer is standing on a scale, they could measure their weight, mg, on the scale. The two forces on the observer are their weight and the normal force, which would be equal in magnitude since the observer is not accelerating. The normal force, read out by the scale, would thus correspond to their weight. To be more precise, the normal force would be equal to mGg, where mG is the gravitational mass of the observer (that mass which is related to the force of gravity experienced by a mass).
If the elevator was instead placed in empty space, and the elevator was accelerating upwards with an acceleration of g (right panel), the observer would still be able to measure their weight by stepping on the scale. The only force on the observer is the normal force from the scale, which must be equal to its mass times their acceleration N=ma=mg, since the observer is accelerating with the elevator. In this case, it is the inertial mass of the observer, mI, that comes into play, so the normal force read on the scale is mIg.
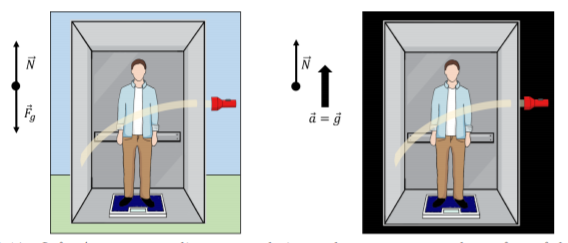
Einstein postulated that it would be impossible for the observer to distinguish whether they are at rest on the surface of the Earth, or in empty space accelerating with an acceleration of g. In other words, he postulated that the inertial and gravitational masses are exactly equivalent. This is what is called the “Equivalence Principle”.
This simple statement has dramatic implications. Special Relativity requires that light will travel in a straight line in empty space. If a beam of light enters and then exits the elevator, the observer on Earth and the one accelerating in empty space must observe the same thing, since they cannot distinguish between being on Earth or accelerating in space. The observer in space, who is accelerating, will observe that the beam of light bends as it crosses the elevator (the beam travels in a straight line as observed in an inertial reference frame, so the person in the accelerating elevator would see it follow a parabolic path). The observer on Earth must thus observe the same thing, namely that light will follow a curved path in the presence of a gravitational field.
But...light must travel in a straight line in empty space. That means that if the path of a beam of light is curved near Earth, it must be because space itself is curved in the presence of a gravitational field! In other words, Einstein’s Theory of General Relativity describes how the presence of mass (or energy) results in a curvature of space (and time).
Imagine a ladybug on the side of a basketball. If the ladybug starts moving in what it believes to be a straight line, it will actually move in a curved path along the surface of the ball, as in Figure 9.4.2. This is like the curved path of light that we observe. If we didn’t know the ball was there, we would just think that the bug was moving along a curved path. In the same way, if an observer is not aware of the curvature of spacetime, it appears that light follows a curved path.
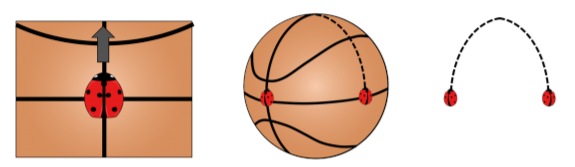
Now imagine there’s a second ladybug. Both bugs start at the middle of the ball and start moving towards the top of the ball in what they think is a straight line (as shown in the center panel of Figure 9.4.2). When the bugs start moving, they are parallel to each other, so if the ball was not curved, the ladybugs would never meet. However, because it is curved, the ladybugs will eventually cross paths. If you were not aware that the ball was there, you would have to conclude that there was some force attracting the bugs to each other, just like if you were unaware that spacetime was curved, you would conclude that massive bodies moving towards each other are attracted by a gravitational force.
Objects that are moving in a gravitational field are actually following Newton’s First Law (they are moving at constant velocity in a straight line and no force is exerted on them). It is strange and unexpected, but high precision measurements confirm that this correctly describes everything that we have measured!
Einstein’s theory was able to describe the orbit of Mercury, and the prediction that gravity leads to light following a curved path was confirmed by Eddington within five years of Einstein’s theory being published. Another implication of the theory is that time goes by slower in the presence of a gravitational field. Clocks on Earth run slower than clocks in orbit (where the gravitational field is weaker). This effect is taken into account when using GPS to determine your position on Earth, since this is based on comparing the time that it takes signals to arrive to your position on Earth from different satellites. This is also somewhat reasonably well described in the movie “Interstallar”, where time is seen to pass much slower for a set of astronauts in the vicinity of a black hole, where the gravitational field is strong.

