12.3: Angular Momentum
- Page ID
- 19449
In this section, we show that we can define a quantity called “angular momentum” as the rotational equivalent of the linear momentum.
Angular Momentum of a Particle
The angular momentum relative to a point of rotation, \(\vec L\), of a particle with linear momentum, \(\vec p\), is defined as:
\[\vec L = \vec r\times \vec p\]
where \(\vec r\) is the vector from the point of rotation to the particle, and the linear momentum, \(\vec p\), is defined relative to an inertial frame of reference in which the point of rotation is at rest.
Consider the time-derivative of angular momentum (where we have to use the product rule for derivatives):
\[\begin{aligned} \frac{d\vec L}{dt} &= \frac{d}{dt} (\vec r\times \vec p)\\[4pt] &=\frac{d\vec r}{dt}\times \vec p + \vec r\times\frac{d\vec p}{dt}\\[4pt] &=\vec v\times \vec p + \vec r\times\frac{d\vec p}{dt}\\[4pt]\end{aligned}\]
The first term is zero, since \(\vec v\) is parallel to \(\vec p\) by definition. Recall Newton’s Second Law written using linear momentum:
\[\begin{aligned} \frac{d\vec p}{dt} = \vec F^{net}\end{aligned}\]
where \(\vec F^{net}\) is the net force on the particle relative to the point of rotation. The rate of change of angular momentum is thus given by:
\[\begin{aligned} \frac{d\vec L }{dt} &= \vec r\times\frac{d\vec p}{dt}\\[4pt] &=\vec r\times\vec F^{net}\end{aligned}\]
where the term on the right is the net torque on the particle. Thus, the rate of change of angular momentum is given by:
\[\frac{d\vec L}{dt}=\vec\tau ^{net}\]
which is analogous to the linear case, but we used angular momentum instead of linear momentum and net torque instead of net force. The net torque on a particle is thus equal to the rate of change of its angular momentum. In particular, the angular momentum of a particle will remain constant (not change with time) if the net torque on the particle is zero.
We can also define the angular momentum of a particle using only angular quantities:
\[\begin{aligned} \vec L = \vec r \times \vec p = m \vec r \times \vec v = mr^2 \vec\omega\end{aligned}\]
where we factored the mass \(m\) out of the momentum and used the definition \(\vec \omega = 1/r^2(\vec r \times \vec v)\). We can think of \(mr^2\) as the moment of inertia, \(I\), of the particle and write:
\[\vec L = mr^{2}\vec\omega = I\vec\omega\]
which is a close analogue to the definition of linear momentum, but we use moment of inertia instead of mass and angular velocity instead of velocity.
The angular momentum is thus parallel to the angular velocity of the particle about the point of rotation. If no net torque is exerted on the particle about that point, then the particle’s angular momentum about that point will remain constant. We can also consider the torque and angular momentum about an axis instead of a point; in that case, we would simply take the components of torque and angular momentum that are parallel to that axis.
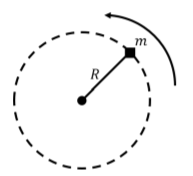
A small block of mass \(m\) attached to a mass-less string is moving along a circle of radius \(R\) on a horizontal table, as depicted from above in Figure \(\PageIndex{1}\). If the table is frictionless: are the block’s linear and/or angular momentum with respect to the axis of rotation conserved? If there is friction between the table and the block, are the block’s linear and/or angular momentum with respect to the axis of rotation conserved? What can you say about the kinetic energy of the block in the two cases?
Solution
If there is no friction between the block and the table, then the forces exerted on the block are:
- \(\vec F_g\), the block’s weight, exerted downwards, with magnitude \(mg\).
- \(\vec N\), a normal force, exerted upwards, with magnitude \(mg\).
- \(\vec T\), a force of tension, exerted towards the center of the circle.
All of these forces are perpendicular to the (tangential) displacement of the block along the circle. Thus, there can be no work done on the block and its speed, \(v\), must remain constant. The kinetic energy of the block must thus remain constant.
The sum of the forces on the block must be towards the center of the circle, since the block is in uniform circular motion. The linear momentum of the block cannot be conserved if there is a net force on the block (and clearly, the block’s velocity vector changes direction as it goes around the circle).
The forces of weight and the normal force are both outside of the plane of motion, and thus cannot exert a torque along the axis of rotation. They are also equal and opposite in magnitude so the net torque from those two forces is always zero (since the net force from those forces is zero). The force of tension is always anti-parallel to the vector \(\vec r\), from the axis of rotation to the particle, and cannot result in a torque about the rotation axis. Thus, the net torque on the block is zero and its angular momentum must be conserved.
If there is kinetic friction exerted by the table on the block, then there is an additional force, \(\vec f_s\), exerted on the block in the direction opposite of motion (tangent to the circle, in the opposite direction from the block’s velocity).
The force of friction will do negative work on the block, slowing it down and reducing its kinetic energy, which is no longer conserved. The net force on the block is non-zero, so its linear momentum is still not conserved. Finally, the force of friction, which is always perpendicular to \(\vec r\), will result in a torque that reduces the angular velocity of the block. The block’s angular momentum is thus no longer conserved when there is friction between the table and the block.
Discussion
In this example, we saw that kinetic energy, linear momentum, and angular momentum are all conserved under different conditions. Kinetic energy is conserved if no net work is done on the block. Linear momentum is conserved if the net force on the block is zero. Angular momentum is conserved if the net torque on the block is zero. By introducing angular momentum, we are able to use a new conserved quantity to help us model rotational dynamics.
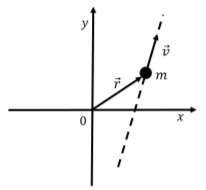
A particle is moving with constant velocity \(\vec v\) (in a straight line) relative to a coordinate system in an inertial frame of reference, as shown in Figure \(\PageIndex{2}\). Show that its angular momentum about the origin is conserved.
Solution
In this case, the particle is moving in a straight line, but we can still define its angular momentum relative to the origin. If \(\vec r\) is the position vector of the particle relative to the origin, its angular momentum is:
\[\begin{aligned} \vec L = \vec r \times \vec p\end{aligned}\]
We can take the time derivative of the angular momentum to see if it changes with time:
\[\begin{aligned} \frac{d\vec L}{dt} = &= \frac{d}{dt} (\vec r\times \vec p)\\[4pt] &=\frac{d\vec r}{dt}\times \vec p + \vec r\times\frac{d\vec p}{dt}\\[4pt] &=\vec v\times \vec p + \vec r\times\frac{d\vec p}{dt}\\[4pt]\end{aligned}\]
The first term is zero because \(\vec v\) and \(\vec p\) are parallel (so their cross-product must be zero). The second term is zero because the particle’s momentum is constant in time (since its velocity is constant). Thus, the particle’s angular momentum does not change with time, and it is conserved.
Discussion
Of course, we expected this result since no net torque is exerted on the particle. It is however worth highlighting that a particle does not need to be rotating for its angular momentum about a given axis to be defined or conserved; all that matters is that there is no net torque on the particle relative to that axis.
Angular momentum of an object or system
Consider a system made of many particles of mass, \(m_i\), each with a position, \(\vec r_i\), and velocity, \(\vec v_i\), relative to a point of rotation that is fixed in an inertial frame of reference.
We can write Newton’s Second Law using the angular momentum, \(\vec L_i\), for particle \(i\):
\[\begin{aligned} \frac{d\vec L_i}{dt} = \vec \tau_i^{net}\end{aligned}\]
where \(\vec \tau_i^{net}\) is the net torque exerted on particle \(i\). We can sum each side of this equation for all of the particles in the system:
\[\begin{aligned} \frac{d\vec L_1}{dt} + \frac{d\vec L_2}{dt} + \frac{d\vec L_3}{dt} + \dots &= \vec \tau_1^{net} + \vec \tau_2^{net} +\vec \tau_3^{net} + \dots\\[4pt] \therefore \frac{d}{dt} \sum_i\vec L_i &= \sum_i \vec \tau_i^{net}\end{aligned}\]
The sum of all of the torques on all of the particles will include a sum over torques that are internal to the system and torques that are external to the system. The sum over internal torques is zero:
\[\begin{aligned} \sum_i \vec\tau_i^{net} = \sum_i \vec\tau_i^{int} + \sum_i \vec\tau_i^{ext} = \sum_i \vec\tau_i^{ext} = \vec\tau^{ext}\end{aligned}\]
where we defined, \(\vec\tau^{ext}\), to be the net external torque exerted on the system. We also introduce the total angular momentum of the system, \(\vec L\), as the sum of the angular momenta of the individual particles:
\[\begin{aligned} \vec L = \sum_i\vec L_i\end{aligned}\]
The rate of change of the total angular momentum of the system is then given by:
\[\frac{d\vec L}{dt}=\vec\tau^{ext}\]
Up to this point, we did not require that the system be a solid object, so the particles in the system can move relative to each other. For example, the particles could be the Sun, planets, and everything else that is in our Solar System. The total angular momentum of all of the bodies in the Solar System (say, relative to the Sun) is conserved if there is no net torque on the solar system relative to the Sun (i.e. if there is no torque about the Sun exerted on any of the bodies in the system that is not exerted by one of the other bodies in the system).
Now, consider a solid object that is modelled as a system of many particles of mass, \(m_i\), at position, \(\vec r_i\), with velocity, \(\vec v_i\), relative to a fixed axis of rotation. We can define the angular momentum of a single particle as (Equation 12.3.3):
\[\begin{aligned} \vec L_i = m_i r_i^2 \vec \omega_i^2\end{aligned}\]
The total momentum of the system is the sum of the angular momenta of the individual particles:
\[\begin{aligned} \vec L &= \sum_i\vec L_i = \sum_i m_i r_i^2 \vec \omega_i^2\end{aligned}\]
Because all of the particles are part of the same object, they must all move in unison and have the same angular velocity, \(\vec\omega\), relative to the axis of rotation. We can thus define the angular momentum about the rotation axis for a solid object with angular velocity, \(\vec\omega\), as:
\[\vec L = \left(\sum_{i} m_{i}r_{i}^{2} \right) \vec\omega = I\vec\omega\]
where we recognized that the sum in parentheses is simply the moment of inertia of the object relative to the axis of rotation. Again, it should be emphasized that this is the total angular momentum of the object about an axis of rotation, and not about a point.
Visualizing the torque and angular momentum of a system can be challenging because it almost always requires visualizing something in three dimensions. Consider a wheel (e.g. a bicycle wheel) that is spinning about horizontal axle which you hold with your hands, as illustrated in the left panel of Figure \(\PageIndex{3}\) (without the hands). Imagine that you are holding onto the axle so that the wheel is front of you, your right hand is to the right of the wheel and your left hand is to the left of the wheel.
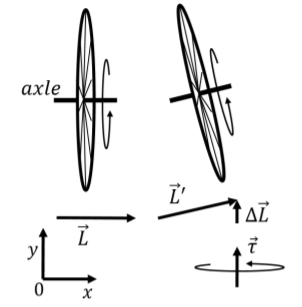
We define a coordinate system as shown so that the wheel is spinning as shown in the left panel, with angular velocity (and angular momentum) in the positive \(x\) direction (the top of the wheel is coming towards you).
You then try to lift your right hand while lowering your left hand in order to tilt the rotation axis, as shown in the right panel. In doing so, you change the direction of the angular momentum (and angular velocity) of the wheel such that the angular momentum, \(\vec L'\), now has a vertical component, \(\Delta \vec L\), as shown. The torque that is required in order to change the angular momentum is given by:
\[\begin{aligned} \vec \tau = \frac{d\vec L}{dt} \sim \frac{\Delta \vec L}{\Delta t}\end{aligned}\]
where \(\Delta t\) is the time that it takes to change the axis of rotation. The torque required in order to change the axis of rotation is directed in the same direction as \(\Delta \vec L\) (the positive \(y\) direction). That is, you will not be able to simply tilt the axle as shown; if you want to tilt the axle, you will also need to push forward with you right hand and pull backwards with your left hand to exert the required torque (shown in the bottom right of the figure)! If you simply try to tilt the rotation axis, your right hand will be pushed towards you and your left hand away from you, as a reaction to the torque that would otherwise be required to tilt the axis!
Conservation of angular momentum
In the previous section, we saw that the net external torque that is exerted on an object (or system) is equal to the rate of change of its angular momentum:
\[\begin{aligned} \frac{d\vec L}{dt} = \vec \tau^{ext}\end{aligned}\]
where the angular momentum and torque are measured about the same axis or point of rotation, fixed in an inertial frame of reference.
The total angular momentum of a system about a point of rotation is conserved (i.e. does not change with time) if there is no net external torque exerted on the system about that point. If one makes the system large enough, then all of the torques can be taken to be internal, and the angular momentum of the system is conserved. The angular momentum of the Universe about a fixed point is thus conserved.
Conservation of angular momentum is another conservation law that we derived from Newton’s Second Law. In the modern formulation of physics, we understand that the conservation of angular momentum is associated with rotational symmetry of Newton’s Second Law; it does not matter from which “angle” we model a system, we can always use Newton’s Second Law. Similarly, conservation of linear momentum is associated with translational symmetry and conservation of energy is associated with the fact that Newton’s Second Law does not change with time. Angular momentum is fundamentally different than linear momentum and energy, and is conserved under different conditions. The angular momentum of a system about a given axis/point is conserved if there is no net torque on the system about that axis/point.
During a spin, a figure skater brings his arms close to his body and increases his angular velocity from \(\omega_1\) to \(\omega_2\). By what fraction did his moment of inertia decrease in doing so?
Solution
We can consider the rotation axis to be vertical through the center of the skater. When the figure skater is spinning, there is no net external torque on him. Thus, his angular momentum is conserved as he bring his arms in. As he bring his arms in, his moment of inertia decreases, since he is bringing the mass of his arms closer to the axis of rotation. If \(I_1\) and \(I_2\) are the moments of inertia of the skater before and after brining his arms in, respectively, we can write the angular momentum about his axis of rotation as:
\[\begin{aligned} L_1 &= I_1\omega_1\\[4pt] L_2 &= I_2\omega_2\end{aligned}\]
Since there is no external torque on the skater, the angular momentum is the same before and after he changes his moment of inertia:
\[\begin{aligned} L_1 &= L_2\\[4pt] I_1\omega_1 &= I_2\omega_2\\[4pt] \therefore \frac{I_1}{I_2} &= \frac{\omega_2}{\omega_1}\end{aligned}\]
Discussion
A spinning figure skater is a good example of the conservation of angular momentum. By changing their shape, they can change their moment of inertia and thus their angular velocity.
Show that Kepler’s Second Law is equivalent to a statement about conservation of the angular momentum of a planet orbiting the Sun.
Solution
Kepler’s Second Law states that in a period of time \(\Delta t\), the area, \(\Delta A\), that is swept out by a planet is constant, regardless of where it is along its orbit. In other words:
\[\begin{aligned} \frac{\Delta A}{\Delta t} = \text{constant}\end{aligned}\]
Figure \(\PageIndex{4}\) shows a planet in an elliptical orbit around the sun.
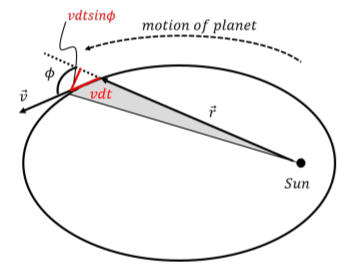
At some point in time, the planet has a velocity vector \(\vec v\) and position vector \(\vec r\) relative to the Sun. In a small period of time \(dt\), the planet will move along a short distance \(vdt\), which we can take as a straight line if \(dt\) is small enough. Let \(\phi\) be the angle between the velocity and position vectors when these are tail to tail, as illustrated.
The small amount of area, \(dA\), swept out by the planet in a period of time \(dt\), is given by the area of the right angle triangle with height \(r\) and base \(vdt\sin\phi\)1:
\[\begin{aligned} dA = \frac{1}{2} r vdt\sin\phi\end{aligned}\]
The rate at which the area is swept out is thus:
\[\begin{aligned} \frac{dA}{dt} = \frac{1}{2} r v\sin\phi\end{aligned}\]
Consider now the magnitude of the planet’s angular momentum about the Sun:
\[\begin{aligned} L = rp\sin\phi = rmv\sin\phi\end{aligned}\]
where the mass of the planet is \(m\). The rate at which the planet sweeps out the area can be written in terms of the angular momentum of the planet:
\[\begin{aligned} \frac{dA}{dt} &= \frac{1}{2} r v\sin\phi = \frac{L}{2m}\end{aligned}\]
The only force exerted on the planet is the gravitational force from the Sun. That force is always anti-parallel to the vector \(\vec r\) from the Sun to the planet, and cannot result in a torque on the planet about the Sun. Thus, the angular momentum of the planet about the Sun must be conserved, and \(L\) is constant. In turn, this means that the rate at which area is swept out by the planet, which is proportional to \(L\), is also constant. Thus, Kepler’s Second Law is equivalent to saying that the angular momentum of a planet relative to the Sun is constant.
Footnotes
1. This is only exact in the limit of \(dt\to 0\), when the small area from the extra piece outside of the ellipse vanishes.

