12.6: Sample problems and solutions
- Page ID
- 19452
A yo-yo can be modeled as two uniform disks, of radius \(R_{2}\), attached to either side of a smaller uniform disk of radius \(R_{1}\), as in Figure \(\PageIndex{1}\). We can assume that all three disks have a mass \(m\). A mass-less string is wrapped around the smaller disk and then the yo-yo is released. What is the acceleration of the center of mass of the yo-yo as it falls and the string unwinds?
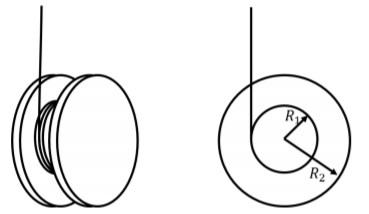
- Answer
-
The forces acting on the yo-yo are
- \(\vec F_{g}\), its weight, with magnitude \(3mg\).
- \(\vec T\), a force of tension from the string
The forces, where they are exerted, and our choice of coordinate system are shown in Figure \(\PageIndex{2}\).
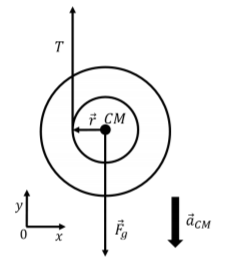
Figure \(\PageIndex{2}\): Free body diagram for the yo-yo. The yo-yo can be modeled as rolling without slipping, as if it were rolling along the string that unwinds. The torque about the center of mass is provided by the tension in the string. The angular acceleration of the yo-yo, \(α\), will be related to the linear acceleration of the center of mass, \(\vec a_{CM}\), since this is rolling without slipping:
\[\begin{aligned} a_{CM}=\alpha R_{1} \end{aligned}\]
where \(R_{1}\) is the radius that is analogous to rolling motion. Since the torque from the force of gravity is zero, we can write Newton’s Second Law for rotational quantities as:
\[\begin{aligned} \vec\tau ^{ext}&=I\vec\alpha \\[4pt] TR_{1}=I\alpha \end{aligned}\]
where \(TR_{1}\) is the magnitude of the torque from the force of tension, since the tension is perpendicular to the vector \(\vec r\) between the center of mass and the point where the tension is exerted. The moment of inertia of the yo-yo about its center of mass is the sum of the moments of inertia of the three disks about their axis of symmetry:
\[\begin{aligned} I = \frac{1}{2}MR_{2}^{2} +\frac{1}{2}MR_{2}^{2} +\frac{1}{2}MR_{1}^{2} =\frac{1}{2}M(2R_{2}^{2}+R_{1}^{2} \end{aligned}\]
We can also write Newton’s Second Law in the vertical direction for the yo-yo (of mass \(3M\)):
\[\begin{aligned} \sum F_{y} &=-F_{g}+T=-3Ma_{CM} \\[4pt] -3MG +T &=-3Ma_{CM} \end{aligned}\]
where we \(a_{CM}\) is the magnitude of the acceleration of the center of mass (since we included the sign in the first equation).
We can eliminate the unknown force of tension from the equations by substitution. Using the equation from Newton’s Second Law:
\[\begin{aligned} T=3M(g-a_{CM}) \end{aligned}\]
and substituting this into the rotational equation:
\[\begin{aligned} TR_{1}&=I\alpha \\[4pt] 3M(g-a_{CM})R_{1}&=I\alpha \end{aligned}\]
We can solve for \(a_{CM}\) by using the condition for rolling without slipping \((αR_{1} = a_{CM})\):
\[\begin{aligned} 3M(g-a_{CM})R_{1}&=I\frac{a_{CM}}{R_{1}} \\[4pt] \frac{I}{R_{1}}a_{CM}+3MR_{1}a_{CM} &=3MgR_{1} \\[4pt] a_{CM}\left( \frac{I}{R_{1}}+3MR_{1} \right) &=3MgR_{1} \\[4pt] a_{CM}&=\frac{3MgR_{1}}{\frac{I}{R_{1}}+3MR_{1}} \\[4pt] &=\frac{3MgR_{1}}{\frac{\frac{1}{2} M(2R_{2}^{2}+R_{1}^{2})}{R_{1}} + 3MR_{1}} \\[4pt] &= \left(\frac{3R_{1}^{2}}{\frac{1}{2}(2R_{2}^{2}+R_{1}^{2})+3R_{1}^{2}} \right) g \\[4pt] \therefore a_{CM} &= \left(\frac{3R_{1}^{2}}{R_{2}^{2}+\frac{7}{2}R_{1}^{2}} \right) g \end{aligned}\]
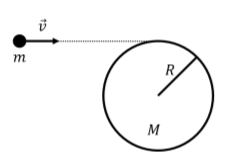
A projectile of mass \(m\) is fired towards a stationary disk of radius \(R\) and mass \(M\) that lies on a horizontal table, as depicted from above in Figure \(\PageIndex{3}\). The disk is in the horizontal plane and can rotate about a vertical axis through its center. The axle about which the disk rotates is attached to the table and cannot move. The projectile’s velocity, \(\vec v\), is horizontal and such that the projectile embeds itself at the edge of the disk. What is the angular velocity of the disk, about its center, after the projectile has embedded itself into the disk? Was the collision elastic? Was linear momentum conserved during the collision?
- Answer
-
We consider the projectile and disk as a system, and a rotation axis that passes through the center of disk. There are no external torques exerted on the system about the rotation axis, so the angular momentum of the system must be conserved through the collision. Before the collision, only the projectile has angular momentum about the axis of rotation, so the magnitude of the angular momentum before the collision is:
\[\begin{aligned} L=rp\sin\phi \end{aligned}\]
where \(φ\) is the angle between the particle’s momentum, \(\vec p = m\vec v\), and a vector, \(\vec r\), from the axis of rotation to the particle. We can calculate the particle’s angular momentum just before the collision, so that \(\vec r\) is the vector from the center of the circle to the point where the particle collides (with magnitude \(R\), and perpendicular to \(\vec v\)). The initial angular momentum of the system is thus:
\[\begin{aligned} L=rp=Rmv \end{aligned}\]
After the collision, the projectile is embedded in the disk. The resulting object has a moment of inertia given by:
\[\begin{aligned} I = I_{disk}+I_{particle}=\frac{1}{2}MR^{2}+mR^{2} \end{aligned}\]
After the collision, the angular momentum of the disk with the embedded projectile is given by:
\[\begin{aligned} L' = I\omega = \left(\frac{1}{2}M+m \right) R^{2}\omega \end{aligned}\]
Using conservation of angular momentum, the angular velocity of the disk after the collision is:
\[\begin{aligned} L&=L' \\[4pt] Rmv&=\left(\frac{1}{2}M+m \right)R^{2}\omega \\[4pt] \therefore\omega &=\frac{mv}{\left(\frac{1}{2}M+m \right)R} \end{aligned}\]
We do not expect that mechanical energy is conserved during the collision, since the projectile embeds itself, which must cost energy. The mechanical energy before the collision is given by the kinetic energy of the projectile:
\[\begin{aligned} E=\frac{1}{2}mv^{2} \end{aligned}\]
After the collision, the kinetic energy is the rotational kinetic energy of the disk with embedded projectile about the axis of rotation:
\[\begin{aligned} E'&=\frac{1}{2}I\omega ^{2}=\frac{1}{2}\left(\frac{1}{2}M+m \right) R^{2}\left( \frac{mv}{(\frac{1}{2}M+m)R} \right)^{2} \\[4pt] &=\frac{1}{2} \frac{m^{2}}{(\frac{1}{2}M+m)}v^{2} \end{aligned}\]
We can see that \(E'\) is less than \(E\), by taking their ratio:
\[\begin{aligned} \frac{E'}{E}&=\frac{\frac{1}{2}\frac{m^{2}}{(\frac{1}{2}M+m)}v^{2}}{\frac{1}{2}mv^{2}} \\[4pt] &=\frac{m}{(\frac{1}{2}M+m)}<1 \end{aligned}\]
and we confirm that mechanical energy is not conserved in the collision (and that energy was lost since one had to deform the projectile and disk).
Linear momentum is clearly not conserved since the final linear momentum is zero, whereas before the collision, it is \(\vec p = m\vec v\). The center of mass of the disk+projectile system moves before the collision and not after. There must thus be a net external force that is exerted on the system. That force is exerted by the table onto the axle of disk, as the disk would otherwise recoil when hit with the projectile.
Discussion
In this example, we used conservation of angular momentum to model a collision. The collision is inelastic, because the projectile embeds itself into the disk. The linear momentum is not conserved through the collision because the axle about which the disk rotates must exert a force on the disk to prevent it from recoiling.

