13.7: Sample problems and solutions
( \newcommand{\kernel}{\mathrm{null}\,}\)
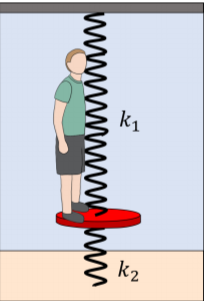
Ty (m=30kg) is trying out a new piece of equipment at his local playground. The equipment consists of a platform that is connected to two springs. The top spring (k1=2400N/m) connects the platform to the playground structure and the bottom spring (k2=3480N/m) (Figure 13.7.1) connects it to the ground. When no one is standing on the platform the platform is 50cm off the ground. When Ty is standing on the platform, he oscillates up and down, and the lowest point that the platform reaches is 35cm off the ground. Show that this is simple harmonic motion and determine what Ty’s maximum speed will be.
- Answer
-
First, we need to solve for the new equilibrium position of the platform, x0, when Ty is standing on the platform. We define the x axis so that the origin is 50cm above the ground (the equilibrium position when no one is standing on the platform) and choose the positive direction to be downwards (Figure 13.7.2).
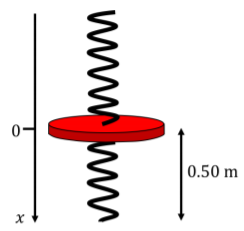
Figure 13.7.2: The platform when no one is standing on it. Even though we do not know the mass of the platform, or the actual resting lengths of the spring, we do not need to know these, since we can model the platform with nobody on it as a single spring with spring constant k=k1+k2 and rest position x=0.
When Ty is standing on the platform, the sum of the forces is given by his weight and the force from the “effective spring”:
∑F=mg−(k1+k2)x
where we noted that, when the platform moves down, both the top and bottom spring will exert a force upwards (Figure 13.7.3).
At equilibrium, the sum of the forces is equal to zero. We can use this to solve for the displacement at x0:
0=mg−(k1+k2)x0∴x0=mgk1+k2=(30kg)(9.8m/s2)(2400Nm)+(3480Nm)=0.05m
We will confirm that this is a simple harmonic oscillator by showing that the system’s motion can be described by the equation:
d2xdt2=−ω2x
For some position x below equilibrium, we can rewrite Newton’s second law as:
ma=mg−(k1+k2)xmd2xdt2=mg−(k1+k2)x
In order to show that this is simple harmonic motion, we need to combine the right hand side of the equation into one term. We found earlier that mg=(k1+k2)x0, which we can use here:
md2xdt2=(k1+k2)x0−(k1+k2)xd2xdt2=(k1+k2)m(x0−x)d2xdt2=−(k1+k2)m(x−x0)
We now define an x′ axis such that x′=x−x0. This means that the origin of the x′ axis is at the new equilibrium position:
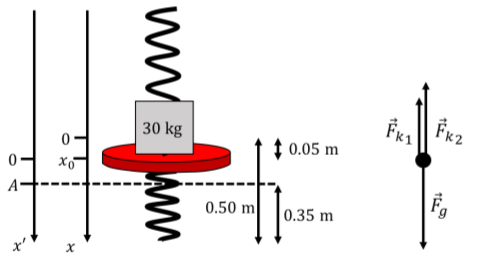
Figure 13.7.3: The forces acting on the platform and our new coordinate system. We can now rewrite our expression using the x′ axis:
d2xdt2=−(k1+k2)mx′
This equation tells us that this is simple harmonic motion about the new equilibrium position, where ω=√(k1+k2)/m. We know that the lowest point that the platform reaches is 35 cm above the ground, which, on our x′ axis, corresponds to x′=10cm (Figure 13.7.3). Thus, the amplitude of the oscillation is A=0.1m. Because this is simple harmonic motion, we know that the position of the platform can be described by the following function:
x′(t)=Acos(ωt+ϕ)
We set t=0 to be when the platform is at its lowest point (x′=A). The value of ϕ is thus:
x′(0)=Acos(ω(0)+ϕ)A=Acos(ϕ)1=cos(ϕ)∴ϕ=0
The velocity is given by:
v(t)=ddtx(t)=−Aωsin(ωt+ϕ)=−Aωsin(ωt)
The speed will be maximized when sin(ωt)=1or−1 . So, the maximum speed will be:
|v|=Aω|v|=A√(k1+k2)m|v|=(0.1m)√(2400Nm+3480Nm)30kg|v|=1.4m/s
A torsional pendulum consists of a horizontal rod suspended from a vertical wire. When the rod is rotated so that it is displaced an angle θ from equilibrium, the wire (which is now twisted) provides a restoring torque about the axis of the wire given by:
τ=−κθ
where κ is the torsion coefficient, which depends on the stiffness of the wire. You may notice that this formula closely resembles Hooke’s law.
a. You construct a torsional pendulum by attaching two small spherical masses (you can assume they are point masses, each of mass m) to the ends of a thin (mass-less) rod of length L and attaching a wire to the center of the rod (Figure 13.7.4). When you displace one of the masses by an angle θ and release it, you find that it oscillates with a period T. Find an expression for the torsion coefficient, κ, in term of T, m, and L.
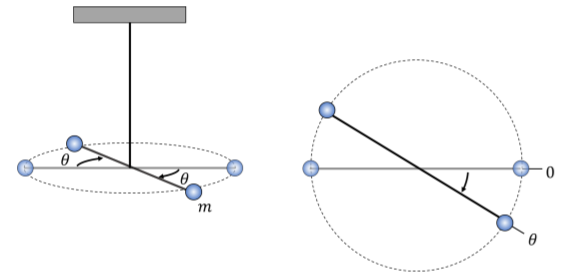
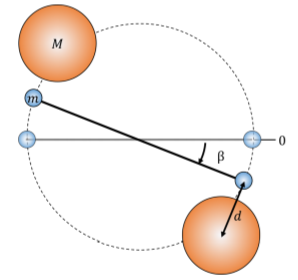
b. You place two very large spheres, each of mass M, near each of the small spheres (as shown in Figure 13.7.5). Each of the small spheres will be acted on by a force of gravity from the nearest large sphere. The pendulum is at equilibrium when it is deflected an angle β from its original equilibrium position. At the new equilibrium, the displacement vectors connecting the centers of large and small spheres have a magnitude d and are essentially perpendicular to the rod. Find an expression for the universal gravitational constant G, in terms of the masses, the length of the rod, and the period measured in part a).
Fun fact! This set-up resembles an experiment performed by Henry Cavendish that was first used to determine the value for G and to test Newton’s Universal Theory of Gravity.
- Answer
-
The only force that creates a torque on the masses is the restoring force from the twisting of the wire. The rotational dynamics version of Newton’s Second Law relates this torque to the angular acceleration, α of the rod:
Iα=−κθ
where I is the moment of inertia of the rod. Rewriting α more explicitly as the second time derivative of the angle, we get:
Id2θdt2=−κθd2θdt2=−κIθ
By inspection, we can see that the torsional pendulum is a simple harmonic oscillator, where ω=√κ/I. The period of the motion is therefore:
T=2πωT=2π√Iκ
We can rearrange this expression to get κ:
T2=4π2Iκκ=4π2IT2
The moment of inertia for one of the masses is m(L/2)2, where L/2 is the distance from the mass to the axis of rotation. The moment of inertia for the two masses attached to the mass-less rod is:
I=2m(L2)2=mL22
Putting this into our expression for κ:
κ=2π2mL2T2
The two forces that provide torques for the small spheres are gravity and the force exerted by the twisting wire. Each of the small spheres will experience a force due to gravity from the nearest large sphere. At equilibrium, the force due to gravity on one of the small spheres is therefore:
Fg=GMmd2
Assuming that, at equilibrium, the force vector is perpendicular to the rod, the torque from one of the large spheres is just the force multiplied by the distance to the axis of rotation. Since there are two large spheres, each of which creates a torque on the pendulum, the total torque due to gravity is:
τg=2FgL2=FgL=GMmd2L
(Note that τg is the torque due to gravity at equilibrium only). We can use Newton’s second law for the pendulum to find an expression for G. At equilibrium, the net torque is equal to zero, and the angle of deflection is β:
τnet=τwire−τg0=τwire−τgτg=τwireGMmd2L=κβ∴G=κβd2LMm
Using our expression for κ found in part a), this becomes:
G=2π2Lβd2MT2

