15.1: Pressure
- Page ID
- 19472
The pressure exerted by a force, \(\vec F\), over a surface with area, \(A\), is a scalar quantity, \(P\), defined as:
\[\begin{aligned} P=\frac{F_{\perp}}{A}\end{aligned}\]
where \(F_{⊥}\) is the component of the force perpendicular to the surface. The SI unit for pressure is the Pascal (Pa). Pressure is related to the area, \(A\), over which a force is exerted, and can be thought of as a measure of how concentrated that force is. For example, a force of \(10\text{ N}\) exerted through a needle (a small area) will result in a much larger pressure than if that force was exerted by a flat hand (a larger area).
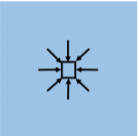
When a force is exerted on a fluid, it creates pressure that we model as being everywhere in the fluid. For each element in the fluid, the pressure from the surrounding fluid exerts an inwards force on the element from all directions (see Figure \(\PageIndex{1}\)). In reaction, the element exerts an outwards force in all directions, and these forces act on neighboring elements.
This is somewhat analogous to the tension that exists everywhere in a rope, where each element of the rope experiences forces from the neighboring elements in rope that try to “pull it apart”. Pressure can be thought of as a “negative” tension, in that the material under pressure is experiencing forces trying to collapse the element onto itself, rather than trying to pull it apart. To create a tension in a rope, one would exert an outwards force on the rope (in order to stretch it), so that the rope exerts an inwards force in reaction. In order to create pressure in a fluid, one must exert an inwards force on the fluid, which then exerts an outwards force in reaction.
If we consider a small cubic volume of fluid, as depicted in the center of Figure \(\PageIndex{1}\), that element of fluid will experience inwards forces in all directions from the pressure in the surrounding fluid, as illustrated by the arrows. If the forces from the pressure result in no net force on the fluid element, then we say that the fluid is in hydrostatic equilibrium, and the element of fluid will be at rest in an inertial frame of reference.
Consider, instead, an element of fluid that at the edge of a container for the fluid (e.g. a cup of water), as depicted in Figure \(\PageIndex{2}\).
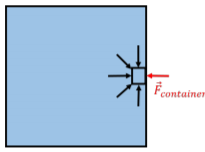
In this case, there is no fluid on the right-hand side of the fluid element to exert a force towards the left. If the fluid element is in equilibrium, it must then be the container that exerts that force, \(\vec F\) container, on the fluid. By Newton’s Third Law, the element of fluid exerts an outwards force on the container. This is true at all points on the surface of container, which will all experience an outwards force from the pressure of the fluid. If the pressure is constant over a surface, the magnitude of the outwards force on the surface will be equal to the pressure of the fluid multiplied by the area of that surface.
If you place an empty sealed tin can under water, the water will exert a pressure on all of the surfaces of the tin can that leads to a net inwards force on all surfaces of the tin can. If the water pressure is high enough, the tin can will get crushed. If, on the other hand, the tin can is allowed to fill with water, it will not get crushed, as the water inside the tin can will have the same pressure as the water outside the tin can and will exert an equal net outwards force on all surfaces of the tin can. The net force on each surface of the can will be zero, and the tin can will not get crushed, no matter how high the water pressure is.
In general, if there is an interface with fluid on either side of it a different pressures, it is the difference in pressure on either side of the interface that determines the net force exerted on the interface, rather than the absolute pressure.
You place a tin can on a table, and use a pump to create a vacuum inside of the can. You observe that the tin can gets crushed. Which explanation is correct?
- By sucking the air out of the can, you also suck in on the walls of the can.
- You lower the pressure inside the can so that the air outside the can exerts a larger inwards force on the can than the outwards force from the air inside the can.
- You lower the pressure inside the can so that the air inside the can exerts a pulling force on the walls of the can.
- All of the above are all valid ways to model this.
- Answer
The effect of gravity
When discussing Figure \(\PageIndex{1}\), we argued that the fluid exerts an equal force, from all directions, on the fluid element, so that the net force on the fluid element is zero. This is not quite correct in the presence of gravity, where the fluid element will have a weight. Thus, if the fluid element is to be in equilibrium, the upwards force (and pressure) from the fluid below must be higher than that from the fluid above the fluid element.
Figure \(\PageIndex{3}\) shows an element of fluid that has a height \(h\) and a surface area \(A\) in the horizontal plane. The pressure, \(P_{2}\), in the fluid below the fluid element must be higher than the pressure, \(P_{1}\), above the fluid element, if the fluid element is in equilibrium.
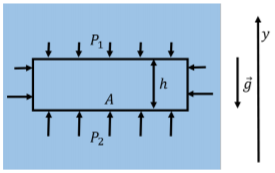
The element of fluid has a total mass, \(m\), given by:
\[\begin{aligned} m = \rho V = \rho Ah \end{aligned}\]
where, \(V = Ah\), is the volume of the fluid, and, \(ρ\), its density.
The net (horizontal) force exerted by the external fluid on the fluid element is zero along the vertical surfaces. Let \(P_{1}\) be the pressure in the fluid above the fluid element, and \(P_{2}\) be the pressure below the fluid element. If we choose a y axis that is positive upwards and the fluid element does not accelerate in the vertical direction, then the y component of Newton’s Second Law, written for the fluid element, is:
\[\begin{aligned} &\sum F_{y} =F_{2}-F_{1}-mg=0 \\[4pt] &P_{2}A-P_{1}A-mg=0 \\[4pt] &P_{2}A-P_{1}A-\rho Ahg=0 \\[4pt] &\therefore P_{2}-P_{1}=\rho gh \end{aligned}\]
where we used the fact that the force resulting from a pressure is given by the pressure multiplied by the area over which it is exerted. We thus find that the difference in pressure due to gravity in a fluid between two positions, \(y_{2}\) and \(y_{1}\), is given by:
\[P(y_{2})-P(y_{1})=-\rho g(y_{2}-y_{1})\]
where the \(y\) axis is defined to increase in the upwards direction. Since the pressure in the fluid depends on the location in the fluid, we say that there is a “pressure gradient” in the fluid.
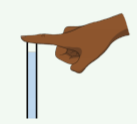
You use your finger to block off the top end of a straw and then remove the straw from a glass of water. What is the most correct description of why the water stays in the straw (Figure \(\PageIndex{4}\)) before you release your finger?
- The straw cannot have vacuum inside of it; unless the finger is removed to let air in to replace the water, the water will remain in the straw.
- There is a small amount of vacuum above the water that sucks the water upwards and prevents it from dropping.
- The pressure of the air in the straw below the water is higher than the pressure of the air in the straw above the water.
- The pressure of the air in the straw below the water is lower than the pressure of the air in the straw above the water.
- Answer
We have assumed that the density of the fluid, \(ρ\), is constant, and that the fluid cannot be compressed. This is a very good approximation for a liquid such as water, but not for a gas, whose density will depend on its pressure. If the fluid were a gas (e.g. a column of air in our atmosphere), both the density and the pressure will change as a function of height. We can easily take this into account in our model, if we consider the fluid element to have a very small height, \(dy\), instead of the finite height, \(h\), as in the derivation above. A fluid element with an infinitesimal height, \(dy\), is illustrated in Figure \(\PageIndex{5}\).
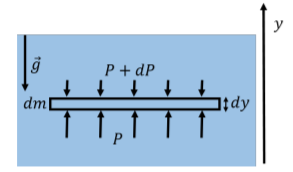
In the very small height, \(dy\), the density of the fluid, \(ρ\), can be taken to be constant, and the infinitesimal element of fluid will have a mass \(dm\):
\[\begin{aligned} dm=\rho Ady \end{aligned}\]
We can model the pressure exerted by the fluid above the fluid element as \(P + dP\), and the pressure exerted by the fluid below as \(P\), where \(dP\) is a small (negative) change in pressure1. The \(y\) component of Newton’s Second Law written for the infinitesimal fluid element is thus:
\[\begin{aligned} \sum F_{y} = PA-(P+dP)A-dmg &=0 \\[4pt] PA-PA-dPA-\rho Adyg&=0 \\[4pt] \therefore - dP - \rho gdy &=0 \end{aligned}\]
We can thus determine how pressure changes with height, \(y\):
\[\frac{dP}{dy}=-\rho g\]
This tells us that the rate of change of pressure with increasing \(y\) is negative; in other words, the pressure decreases as the elevation increases, as we had already concluded. We can integrate the equation to obtain the change in pressure in going from \(y_{1}\) to \(y_{2}\):
\[\begin{aligned} dP&=-\rho gdy \\[4pt] \int_{P_{1}}^{P_{2}}dp&=-\int_{y_{1}}^{y_{2}}\rho gdy \\[4pt] \therefore P_{2}-P_{1}&= - \int_{y_{1}}^{y_{2}}\rho gdy \end{aligned}\]
If the density, \(ρ\), is constant, then this leads to Equation 15.1.1. Note that, thus far, we have only modeled how pressure in a fluid changes with height, but we have not determined the absolute pressure in a fluid.
If we assume that the density of air is proportional to its pressure, how does the density of air change with altitude?
Solution
We know that the rate of change of pressure with altitude (position \(y\), where positive \(y\) is defined to be upwards) is given by:
\[\begin{aligned}\frac{dP}{dy}=-\rho g \end{aligned}\]
Since we can assume that the density is proportional to the pressure, we can introduce an arbitrary constant, \(a\), and state that:
\[\begin{aligned} \rho &=aP \\[4pt] \therefore \frac{dP}{dy}&=\frac{d}{dy}\frac{1}{a}\rho = \frac{1}{a}\frac{d\rho}{dy} \end{aligned}\]
where the constant \(a\) can be evaluated if we know the pressure and density at some point. We can thus write that the rate of change of the density with position \(y\) is given by:
\[\begin{aligned} \frac{1}{a}\frac{d\rho}{dy}&=-\rho g \\[4pt] \therefore \frac{d\rho}{dy}&=-ag\rho \end{aligned}\]
This is a separable differential equation for \(ρ\), allowing us to separate the variables and integrate from, say, an altitude of \(y = 0\), where the density is \(ρ_{0}\), to an altitude \(y\), where the density is \(ρ\):
\[\begin{aligned} \frac{d\rho}{\rho}&=-agdy \\[4pt] \int_{\rho_{0}}^{\rho}\frac{d\rho}{\rho}&=-\int_{0}^{y}agdy \\[4pt] \ln (\rho)-\ln (\rho _{0})&=-agy \\[4pt] \ln\left(\frac{\rho}{\rho _{0}} \right)&=-agy \end{aligned}\]
We can take the exponential on each side of the equation to get rid of the logarithm:
\[\begin{aligned} \frac{\rho}{\rho_{0}}&=e^{-agy} \\[4pt] \therefore \rho (y)&=\rho _{0}e^{-agy} \end{aligned}\]
We thus find that the density of the air decreases exponentially with altitude. This is why it is more difficult to breathe at high altitude. Since we assumed that the density of the air is proportional to its pressure, the air pressure will also decrease exponentially with increasing altitude:
\[\begin{aligned} P(y)=P_{0}e^{-agy} \end{aligned}\]
where \(P_{0}\) is the pressure at an altitude of \(y = 0\). If we know \(P_{0}\) and \(ρ_{0}\), then the constant \(a\) is given by:
\[\begin{aligned} a=\frac{\rho _{0}}{P_{0}} \end{aligned}\]
Discussion
If we applied this model to the Earth’s atmosphere, our model would only provide qualitative agreement, as the density of the air also depends on its temperature and other factors. Nonetheless, it is interesting that, based on the simple requirement that an element of air be in hydrostatic equilibrium, we are able to obtain a reasonable description of how pressure and density change with altitude in the Earth’s atmosphere.
Pascal's Principle
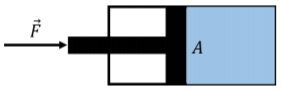
Pascal’s Principle states that if an external pressure is exerted on a fluid, the pressure everywhere in the fluid increases by that amount. For example, if a fluid is contained in a piston with a cross-section area, \(A\), and a force, \(F\), is exerted on the piston (Figure \(\PageIndex{6}\)), then the pressure everywhere in the fluid increase by \(F/A\).
If we wish to determine the absolute pressure in the water at some depth, \(h\), in the ocean, we need to include the fact that the Earth’s atmosphere exerts a net downwards force on the surface of the ocean in addition to the fact that the pressure changes with depth due to gravity. The pressure from the air in the Earth’s atmosphere is called “atmospheric pressure”, and depends on a variety of conditions, such as the weather. The average pressure from the atmosphere is \(P_{0} = 1.013 × 10^{5}\text{ Pa}\). If the atmospheric pressure is \(P_{0}\) at the surface of the ocean, then the pressure at some depth, \(h\), is given by:
\[\begin{aligned} P(h)=P_{0}+\rho gh \end{aligned}\]
where \(ρ\) is the density of water. As a consequence, the pressure at any depth, \(h\), in a fluid is the same everywhere at that depth in the fluid.
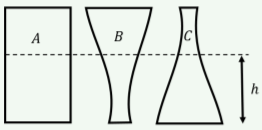
You fill the three glasses in Figure \(\PageIndex{7}\) such that the liquid reaches a height h above the bottom of the glass. What can you say about the pressure of the liquid at the bottom of each glass?
- It is highest for glass \(A\).
- It is highest for glass \(B\).
- It is highest for glass \(C\).
- It is the same for all glasses.
- It is only the same for all glasses if we can neglect atmospheric pressure.
- Answer
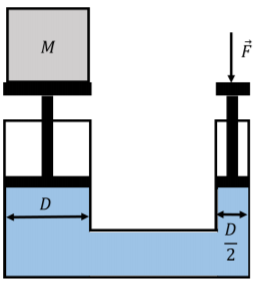
A hydraulic lift exploits Pascal’s principle in order to use a small force to exert a large force. The hydraulic lift in Figure \(\PageIndex{8}\) shows a lift that is constructed by having a fluid between two vertical movable pistons. The pistons are cylindrical and the diameter of their cross-sections are \(D\) and \(D/2\). A mass, \(M\), is placed on the piston with the larger diameter. What is the magnitude of the force, \(\vec F\), that must be applied on the smaller piston in order to lift the mass, \(M\)?
Solution
If a force \(\vec F\) is applied to the small piston, then the pressure in the fluid will increase by:
\[\begin{aligned} \Delta P = \frac{F}{A}=\frac{F}{\pi \frac{D^{2}}{4}}=\frac{4F}{\pi D^{2}}\end{aligned}\]
This will result in a net upwards force, \(\vec F'\), on the large piston, with a magnitude:
\[\begin{aligned} F' = \Delta P A' = \Delta \pi D^{2} = \frac{4F}{\pi D^{2}}\pi D^{2}=4F\end{aligned}\]
Thus the force on the large piston will be four times that exerted on the small piston. One only needs to exert a force with a magnitude of \(Mg/4\) in order to lift the mass, \(M\).
Measuring pressure
In this section, we describe how one can design instruments to measure pressure. The most straightforward device is a manometer, which is constructed using a U-shaped tube filled with a fluid of known density, \(ρ\), as shown in Figure \(\PageIndex{9}\).
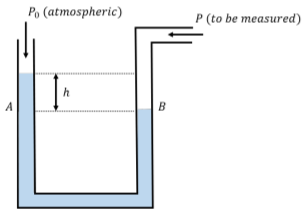
A manometer can be used to measure a pressure \(P\) relative to atmospheric pressure, \(P_{0}\). One end of the tube is open to atmospheric pressure, and the other is connected to the fluid (e.g. a gas) for which we want to measure the pressure. If the pressure being measured is larger than atmospheric pressure, the fluid in the manometer will experience a greater downwards force on the side of the pressure to be measured than on the side open to atmospheric pressure, as shown in Figure \(\PageIndex{9}\). There will be a difference, \(h\), in the level of the fluid on each side of the tube, which is directly proportional to the difference in pressure between the two sides of the tube.
Consider the point in the fluid at location \(B\) in Figure \(\PageIndex{9}\), where the pressure is \(P_{B} = P\), the pressure to be measured. The point in the fluid at location \(A\), which is at the same height in the fluid, must have the same pressure as point \(B\). We can write the pressure at point \(A, P_{A}\), as the sum of the atmospheric pressure and the pressure from the column of water of height, \(h\):
\[\begin{aligned} P_{A}=P_{0}+\rho gh \end{aligned}\]
Since this must also be equal to the pressure at point \(B\), we can find the difference between the pressure we want to measure and atmospheric pressure:
\[\begin{aligned} P_{A}&=P_{B} \\[4pt] P_{0}+\rho gh &=P \\[4pt] \therefore P-P_{0}&=\rho gh \end{aligned}\]
The difference between a pressure and the atmospheric pressure is called “gauge pressure”, and is all that we can measure if we do not know the absolute value of the atmospheric pressure. Using a manometer, the gauge pressure is given by \(ρgh\), whereas the “absolute pressure”, \(P\), is given by adding the atmospheric pressure to the gauge pressure, \(P = P_{0} + ρgh\). Most pressure measuring devices (“pressure gauges”), measure pressure relative to atmospheric pressure, using a similar mechanism.
The atmospheric pressure at a location on Earth varies based on the weather. A barometer is an instrument designed to measure the atmospheric pressure. A simple barometer can be built from a manometer, with one end closed, as illustrated in Figure \(\PageIndex{10}\).
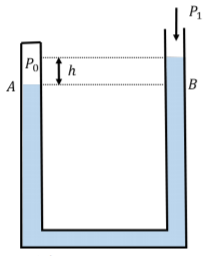
One end of the manometer is sealed on a day where the atmospheric pressure is, say, \(P_{0}\), while the other end of the tube is left open. The height difference, \(h\), between the fluid in either side of the tube is a measure of how different the current atmospheric pressure, \(P_{1}\), is relative to the pressure, \(P_{0}\), when the manometer was sealed. In Figure \(\PageIndex{10}\), the barometer is shown on a day where the atmospheric pressure is lower than on the day the manometer was sealed. The difference in pressure is given by:
\[\begin{aligned} P_{1}=P_{0}+\rho gh \end{aligned}\]
if we define \(h\) to be positive when the side with the pressure \(P_{0}\) is higher (so \(h\) is negative in Figure \(\PageIndex{10}\) and \(P_{1}\) is less than \(P_{0}\)).
We can also measure the absolute atmospheric pressure if we evacuate the air out of the sealed end of the tube, so that \(P_{0} = 0\). When doing so, the difference in height between the fluid on either side of the manometer is a measure of the absolute atmospheric pressure.
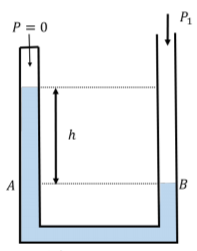
Using a manometer filled with water (\(ρ = 1 × 10^{3} \text{kg/m}^{3}\)), you construct a barometer to measure the absolute atmospheric pressure by evacuating the air from one side of the manometer, as shown in Figure \(\PageIndex{11}\). What is the difference in height, \(h\), when the atmospheric pressure is “nominal”, \(P_{1} = 1.013 × 10^{5}\text{Pa}\)?
Solution
The pressure, \(P_{1}\), on the open side of the manometer is given by:
\[\begin{aligned} P_{B} &=P_{A} \\[4pt] P_{1}&=P_{0}+\rho gh = \rho gh \end{aligned}\]
if the sealed side of the manometer has a pressure, \(P_{0} = 0\), above the fluid. If \(P_{1} = 1.013 × 10^{5}\text{ Pa}\), we can find the height, \(h\):
\[\begin{aligned} h=\frac{P_{1}}{\rho g}=\frac{(1.013\times 10^{5}\text{Pa})}{(1000\text{kg/m}^{3})(9.8\text{m/s}^{2})}=10.3\text{m} \end{aligned}\]
Discussion
The difference in height is about \(10\text{ m}\) when the atmospheric pressure is nominal. This means that the manometer needs to be at least this tall to measure absolute atmospheric pressure, which is not practical to construct! If, instead, one uses a liquid with a higher density than that of water, then this height can be reduced substantially. Traditionally, barometers have been built using mercury, which has a density of (\(ρ_{Hg} = 13.6 × 10^{3}\text{kg/m}^{3}\)), so that the height difference at nominal atmospheric pressure is \(760\text{ mm}\). This is a much easier instrument to build (apart from the safety concerns of using mercury). For this reason, an often-used unit of pressure is “mm of mercury”, which corresponds to the height difference in a manometer that is built using mercury.
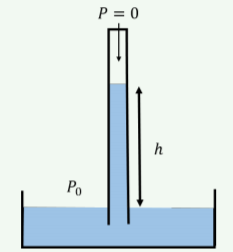
You build a Torricelli barometer, as illustrated in Figure \(\PageIndex{12}\), to measure the absolute atmospheric pressure. The sealed vertical tube has a space at the top that is evacuated (a pressure of zero), so that atmospheric pressure on the container of liquid forces the liquid up the tube to a height, \(h\), which is proportional to atmospheric pressure. If you use olive oil as the liquid, what can you say about the height, \(h\), for nominal atmospheric pressure?
- It is greater than \(10.3\text{ m}\).
- It is equal to \(10.3\text{ m}\).
- It is less than \(10.3\text{ m}\).
- Not enough information to tell.
- Answer
Footnotes
1. We placed the \(dP\) on the top part of the fluid, even though the pressure is higher on the bottom part of the fluid, because the \(y\) axis increases upwards. We are really interested in the change in pressure, \(dP\), that corresponds to a change in height, \(dy\), along the positive \(y\) direction.

