16.2: The Coulomb force
- Page ID
- 19480
Coulomb was the first to provide a detailed quantitative description of the force between charged objects. Nowadays, we use the (derived) SI unit of “Coulomb” (C) to represent charge. The “charge” of an object corresponds to the net excess (or lack) of electrons on the object. An electron has a charge of \(-e=-1.6\times 10^{-19}\text{C}\). Thus, an object with a charge of \(-1\text{C}\) has an excess of about \(-1.6\times 10^{19}\) electrons on it, which is a very large charge. If an object has an excess of electrons, it is negatively charged and we indicate this with a negative sign on the charge of the object. An object with a (positive) charge of \(1\text{C}\) thus has a deficit of \(-1.6\times 10^{19}\) electrons.
Through careful studies of the force between two charged spheres, Coulomb observed1 that:
- The force is attractive if the objects have opposite charges and repulsive if the objects have the same charge.
- The force is inversely proportional to the squared distance between spheres.
- The force is larger if the charges involved are larger.
This leads to Coulomb’s Law for the electric force (or simply “Coulomb’s Law”), \(\vec F_{12}\), exerted on a point charge \(Q_1\) by another point charge \(Q_2\):
\[\vec F_{12}=k\frac{Q_{1}Q_{2}}{r^{2}}\hat r_{21}\]
where \(\hat r_{21}\) is the unit vector from \(Q_2\) to \(Q_1\) and \(r\) is the distance between the two charges, as illustrated in Figure \(\PageIndex{1}\). \(k=8.99\times 10^{9}\text{N}\cdot\text{m}^{2}\text{/C}^{2}\) is simply a proportionality constant (“Coulomb’s constant”) to ensure that the quantity on the right will have units of Newtons when all other quantities are in S.I. units. In some instances, it is more convenient to use the “permittivity of free space”, \(\epsilon_0\), rather than Coulomb’s constant, in which case Coulomb’s Law has the form:
\[\begin{aligned} \vec F_{12}=\frac{1}{4\pi\epsilon_0}\frac{Q_1Q_2}{r^2}\hat r_{21}\end{aligned}\]
where \(\epsilon_{0}=\frac{1}{4\pi k}=8.85\times 10^{-12}\text{C}^{2}\cdot\text{N}^{-1}\cdot\text{m}^{-2}\) is a more fundamental constant, as we will see in later chapters.
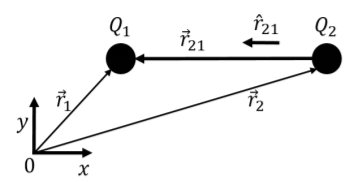
If the two charges have positions \(\vec r_1\) and \(\vec r_2\), respectively, then the vector \(\hat r_{21}\) is given by:
\[\begin{aligned} \hat r_{21} = \frac{\vec r_2 - \vec r_1}{||\vec r_2 - \vec r_1||}\end{aligned}\]
Coulomb’s Law is mathematically identical to the gravitational force in Newton’s Universal Theory of Gravity. Rather than quantity of mass determining the strength of the gravitational force, it is the quantity of charge that determines the strength of the electric force. The only major difference is that gravity is always attractive, whereas the Coulomb force can be repulsive.
The Coulomb force is conservative.
- True.
- False.
- Answer
The product \(Q_1Q_2\) in the numerator of Coulomb’s force is positive if the two charges have the same sign (both positive or both negative) and negative if the charges have opposite signs. Again, referring to Figure \(\PageIndex{1}\), if the two charges are positive, the force on \(Q_1\) will point in the same direction as \(\hat r_{21}\) (since all of the scalars are positive in Coulomb’s Law) and thus be repulsive. If, instead, the two charges have opposite signs, the product \(Q_1Q_2\) will be negative and the force vector on \(Q_1\) will point in the opposite direction from \(\hat r_{21}\) and the force is attractive.
Calculate the magnitude of the electric force between the electron and the proton in a hydrogen atom and compare this to the gravitational force between them.
Solution
We model this by assuming that the electron and proton are point charges a distance of \(1 \unicode{xC5}=1\times 10^{-10}\text{m}\) apart (\(1\) Angstrom is about the size of the hydrogen atom). The proton and electron have the same charge with magnitude \(e=1.6\times 10^{-19}\text{C}\), so the (attractive) electric force between them has a magnitude of:
\[\begin{aligned} F^{e}=k\frac{Q_{1}Q_{2}}{r^{2}}=(9\times 10^{9}\text{N}\cdot \text{m}^{2}\text{/C}^{2})\frac{(1.6\times 10^{-19}\text{C})(1.6\times 10^{-19}\text{C})}{(1\times 10^{-10}\text{m})^{2}}=2.3\times 10^{-8}\text{N} \end{aligned}\]
which is a small number, but acting on a very small mass. In comparison, the force of gravity between an electron (\(m_e=9.1\times 10^{-31}\text{kg}\)) and a proton (\(m_p=1.7\times 10^{-27}\text{kg}\)) is given by:
\[\begin{aligned} F^{g}=G\frac{m_{2}m_{p}}{r^{2}}=(6.7\times 10^{-11}\text{Nm}^{2}\text{/kg}^{2}\frac{(9.1\times 10^{-31}\text{kg})(1.7\times 10^{-27}\text{kg})}{(1\times 10^{-10}\text{m})^{2}}=1.04\times 10^{-47}\text{N} \end{aligned}\]
Discussion
As we can see, the electric force between an electron and a proton is \(39\) orders of magnitude larger than the gravitational force! This shows that the gravitational force is extremely weak on the scale of particles and has essentially no effect in particle physics. Indeed, the best current theory of particle physics, and the most precisely tested theory in physics, the “Standard Model”, does not need to include gravity in order to provide a spectacularly precise description of particles. One of the big challenges in theoretical physics is nonetheless to develop a theory that integrates the gravitational force with the other forces.
Three charges, \(Q_1=1\text{nC}\), \(Q_2=-2\text{nC}\), and \(q=-1\text{nC}\), are held fixed at the three corners of an equilateral triangle with sides of length \(a=1\text{cm}\), with a coordinate system as shown in Figure \(\PageIndex{2}\). What is the electric force vector on charge \(q\)? (Note that \(1\text{nC}=1\times 10^{-9}\text{C}\)).
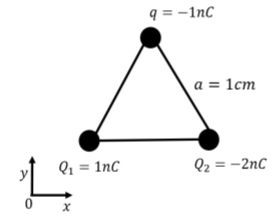
Solution
The net electric force on charge \(q\) will be the vector sum of the forces from charges \(Q_1\) and \(Q_2\). We thus need to determine the force vectors on \(q\) from each charge using Coulomb’s Law, and then add those two vectors to obtain the net force on \(q\). The force vectors exerted on \(q\) from each charge are illustrated in Figure \(\PageIndex{3}\).
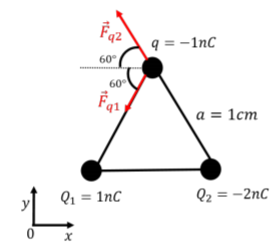
The force from charge \(Q_1\) has magnitude:
\[\begin{aligned} F_{q1}= \left|k\frac{Q_{1}q}{a^{2}} \right|=(9\times 10^{9}\text{N}\cdot\text{M}^{2}\text{/C}^{2})\frac{(1\times 10^{-9}\text{C})(1\times 10^{-9}\text{C})}{(0.01\text{m})^{2}}=9\times 10^{-5}\text{N} \end{aligned}\]
and components:
\[\begin{aligned} \vec F_{q1}&=-F_{q1}\cos(60^{\circ})\hat x-F_{q1}\sin(60^{\circ})\hat y\\[4pt] &=-(4.5\times 10^{-5}\text{N})\hat x-(7.8\times 10^{-5}\text{N})\hat y\end{aligned}\]
Similarly, the force on \(q\) from \(Q_2\) has magnitude:
\[\begin{aligned} F_{q2}=\left |k\frac{Q_2q}{a^2}\right |=(9\times 10^{9}\text{N}\cdot \text{m}^2\text{/C}^{2})\frac{(2\times 10^{-9}\text{C})(1\times 10^{-9}\text{C})}{(0.01\text{m})^2}=1.8\times 10^{-4}\text{N}\end{aligned}\]
and components:
\[\begin{aligned} \vec F_{q2}&=-F_{q2}\cos(60^{\circ})\hat x+F_{q2}\sin(60^{\circ})\hat y\\[4pt] &=-(9.0\times 10^{-5}\text{N})\hat x+(1.6\times 10^{-4}\text{N})\hat y\end{aligned}\]
Finally, we can add the two force vectors together to obtain the net force on \(q\):
\[\begin{aligned} \vec F^{net}&=\vec F_{q1}+\vec F_{q2}\\[4pt] &=-(4.5\times 10^{-5}\text{N})\hat x-(7.8\times 10^{-5}\text{N})\hat y-(9.0\times 10^{-5}\text{N})\hat x+(1.6\times 10^{-4}\text{N})\hat y\\[4pt] &=-(13.5\times 10^{-5}\text{N})\hat x+(8.2\times 10^{-5}\text{N})\hat y\end{aligned}\]
which has a magnitude of \(15.8\times 10^{-5}\text{N}\).
Discussion
In this example, we determined the net force on a charge by making use of the superposition principle; namely, that we can treat the forces exerted on \(q\) by \(Q_1\) and \(Q_2\) independently, without needing to consider the fact that \(Q_1\) and \(Q_2\) exert forces on each other.
Footnotes
1. Others had initially observed the inverse square law for the electric force, but Coulomb was the first to formalize the theory.