17.2: Gauss’ Law
( \newcommand{\kernel}{\mathrm{null}\,}\)
Gauss’ Law is a relation between the net flux through a closed surface and the amount of charge, Q^{enc}, in the volume enclosed by that surface:
\oint\vec E\cdot d\vec A=\frac{Q^{enc}}{\epsilon_{0}}
In particular, note that Gauss’ Law holds true for any closed surface, and the shape of that surface is not specified in Gauss’ Law. That is, we can always choose the surface to use when calculating the flux. For obvious reasons, we often call the surface that we choose a “gaussian surface”. But again, this surface is simply a mathematical tool, there is no actual property that makes a surface “gaussian”; it simply means that we chose that surface in order to apply Gauss’ Law. In Example 17.1.3 above, we confirmed that Gauss’ Law is compatible with Coulomb’s Law for the case of a point charge and a spherical gaussian surface.
Physically, Gauss’ Law is a statement that field lines must begin or end on a charge (electric field lines originate on positive charges and terminate on negative charges). Recall, flux is a measure of the net number of lines coming out of a surface. If there is a net number of lines coming out of a closed surface (a positive flux), that surface must enclose a positive charge from where those field lines originate. Similarly, if there are the same number of field lines entering a closed surface as there are lines exiting that surface (a flux of zero), then the surface encloses no charge. Gauss’ Law simply states that the number of field lines exiting a closed surface is proportional to the amount of charge enclosed by that surface.
Primarily, Gauss’ Law is a useful tool to determine the magnitude of the electric field from a given charge, or charge distribution. We usually have to use symmetry to determine the direction of the electric field vector. In general, the integral for the flux is difficult to evaluate, and Gauss’ Law can only be used analytically in cases with a high degree of symmetry. Specifically, the integral for the flux is easiest to evaluate if:
- The electric field makes a constant angle with the surface. When this is the case, the scalar product can be written in terms of the cosine of the angle between \vec E and d\vec A, which can be taken out of the integral if it is constant:
\begin{aligned} \oint \vec E\cdot d\vec A=\oint E\cos\theta dA=\cos\theta\oint EdA\end{aligned}
Ideally, one has chosen a surface such that this angle is 0 or 180^{\circ}.
- The electric field is constant in magnitude along the surface. When this is the case, the integral can be simplified further by factoring out, E, and simply becomes an integral over dA (which corresponds to the total area of the surface, A):
\begin{aligned} \oint \vec E\cdot d\vec A=\cos\theta\oint EdA =E\cos\theta\oint dA=EA\cos\theta \end{aligned}
Ultimately, the points above should dictate the choice of gaussian surface so that the integral for the flux is easy to evaluate. The choice of surface will depend on the symmetry of the problem. For a point (or spherical) charge, a spherical gaussian surface allows the flux to easily be calculated (Example 17.1.3). For a line of charge, as we will see, a cylindrical surface results is a good choice for the gaussian surface. Broadly, the steps for applying Gauss’ Law to determine the electric field are as follows:
- Make a diagram showing the charge distribution.
- Use symmetry arguments to determine in which way the electric field vector points.
- Choose a gaussian surface that goes through the point for which you want to know the electric field. Ideally, the surface is such that the electric field is constant in magnitude and always makes the same angle with the surface, so that the flux integral is straightforward to evaluate.
- Calculate the flux, \oint \vec E\cdot d\vec A.
- Calculate the amount of charge located within the volume enclosed by the surface, Q^{enc}.
- Apply Gauss’ Law, \oint \vec E\cdot d\vec A=\frac{Q^{enc}}{\epsilon_0}.
An insulating sphere of radius, R, contains a total charge, Q, which is uniformly distributed throughout its volume. Determine an expression for the electric field as a function of distance, r, from the center of the sphere.
Solution
Note that this is identical, mathematically, to the derivation that was done in Section 9.2 for the case of gravity.
When applying Gauss’ Law, we first need to think about symmetry in order to determine the direction of the electric field vector. We also need to think about all possible regions of space in which we need to determine the electric field. In particular, for this case, we need to determine the electric field both inside (r\leq R) and outside (r\geq R) of the charged sphere.
Figure \PageIndex{1} shows the charged sphere of radius R. If we consider the direction of the electric field outside the sphere (where \vec E_{out} is drawn), we realize that it can only point in the radial direction (towards or away from the center of the sphere), as this is the only choice that preserves the symmetry of the sphere. Being a sphere, the charge looks the same from all angles; thus, the electric field must also look the same from all angles, otherwise, there would be a preferred orientation for the sphere. The same argument holds for the electric field vector inside the sphere (drawn as \vec E_{in}).
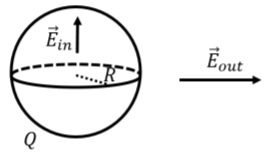
We now need to choose a gaussian surface that will make the flux integral easy to evaluate. Ideally, we can find a surface over which the electric field makes the same angle with the surface and over which the electric field is constant in magnitude. Again, based on the symmetry of the charge distribution, it is clear that a spherical surface of radius, r, will satisfy these properties.
We start by applying Gauss’ Law outside the charge (with r\geq R) to determine the electric field, \vec E_{out}. Figure \PageIndex{2} shows our choice of spherical gaussian surface (labeled S) of radius, r, which is concentric with the spherical charge distribution of radius, R, and total charge, +Q.
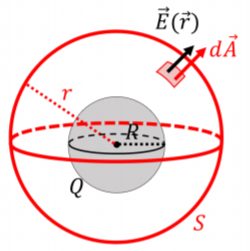
In order to apply Gauss’ Law, we need to calculate:
- the net flux through the surface.
- the charge in the volume enclosed by the surface.
The net flux through the surface is found in the same way as in Example 17.1.3, and is given by:
\begin{aligned} \Phi_E&=\oint \vec E\cdot d\vec A=\oint E dA= E\oint dA=E(4\pi r^2)\end{aligned}
where our choice of spherical surface led to \vec E\cdot d\vec A=EdA, since \vec E and d\vec A are always parallel. Furthermore, by symmetry, the electric field must be constant in magnitude along the whole surface, or the spherical symmetry would be broken. This allowed us to factor the E out of the integral, leaving us with, \oint dA, which is simply the area of our gaussian spherical surface, 4\pi r^2.
The gaussian surface with r\geq R encloses the whole charged sphere, so the charge enclosed is simply the charge of the sphere, Q^{enc}=Q. Applying Gauss’ Law allows us to determine the magnitude of the electric field:
\begin{aligned} \oint \vec E\cdot d\vec A&=\frac{Q^{enc}}{\epsilon_0} \\[4pt] E(4\pi r^2) &= \frac{Q}{\epsilon_0}\\[4pt] \therefore E&= \frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\end{aligned}
which is the same as the electric field a distance r from a point charge. Thus, from the outside, a spherical charge distribution leads to the same electric field as if the charge were concentrated at the center of the sphere.
Next, we determine the magnitude of the electric field inside the charged sphere. In this case, we choose a spherical gaussian surface of radius r\leq R, that is concentric with the sphere, as illustrated by the surface labeled, S, that is shown in Figure \PageIndex{3}.
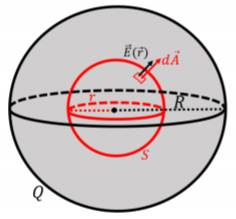
The flux integral is trivial again, since the electric field always makes the same angle with the gaussian surface, and the magnitude of the electric field is constant in magnitude along the surface:
\begin{aligned} \Phi_E&=\oint \vec E\cdot d\vec A=\oint E dA= E\oint dA=E(4\pi r^2)\end{aligned}
In this case, however, the charge in the volume enclosed by the gaussian surface is less than Q, since the whole charge is not enclosed. We are told that the charge is distributed uniformly throughout the spherical volume of radius R. We can thus define a volume charge density, \rho, (charge per unit volume) for the sphere:
\begin{aligned} \rho=\frac{Q}{V}=\frac{Q}{\frac{4}{3}\pi R^3}\end{aligned}
The volume enclosed by the gaussian surface is \frac{4}{3}\pi r^3, thus, the charge, Q^{enc}, contained in that volume is given by:
\begin{aligned} Q^{enc}=\frac{4}{3}\pi r^3 \rho=\frac{4}{3}\pi r^3 \frac{Q}{\frac{4}{3}\pi R^3}=Q\frac{r^3}{R^3}\end{aligned}
Finally, we apply Gauss’ Law to find the magnitude of the electric field inside the sphere:
\begin{aligned} \oint \vec E\cdot d\vec A&=\frac{Q^{enc}}{\epsilon_0} \\[4pt] E(4\pi r^2) &=\frac{Q}{\epsilon_0}\frac{r^3}{R^3}\\[4pt] \therefore E&= \frac{Q}{4\pi\epsilon_0R^3}r\end{aligned}
Note that the electric field increases linearly with radius inside of the charged sphere, and then decreases with radius squared outside of the sphere. Also, note that at the center of the sphere, the electric field has a magnitude of zero, as expected from symmetry.
Discussion
In this example, we showed how to use Gauss’ Law to determine the electric field inside and outside of a uniformly charged sphere. We recognized the spherical symmetry of the charge distribution and chose to use a spherical surface in order to apply Gauss’ Law. This, in turn, allowed the flux to be easily calculated. We found that outside the sphere, the electric field decreases in magnitude with radius squared, just as if the entire charge were concentrated at the center of the sphere. Inside the sphere, we found that the electric field is zero at the center, and increases linearly with radius.
A thin charged spherical shell carries a uniformly distributed charge of +Q.
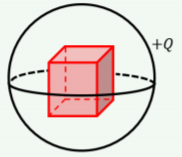
If we place a cube inside the shell, as shown in Figure \PageIndex{4}, what is the total flux out of the surface of the cube?
- \frac{Q}{12\pi}\text{Vm}.
- \frac{Q}{2\pi}\text{Vm}.
- \frac{Q}{6}\text{Vm}.
- 0\text{Vm}.
- Answer
-
An infinitely long straight wire carries a uniform charge per unit length, \lambda. What is the electric field at a distance, R, from the wire?
Solution
We start by making a diagram of the charge distribution, as in Figure \PageIndex{5}, so that we can use symmetry arguments to determine the direction of the electric field vector. The electric field vector could be either:
- in the radial direction (point to/from the center of the wire).
- such that electric field lines form concentric circles with the wire.
- co-linear with the wire.
In all three possibilities above, you would not be able to infer that one particular direction in the plane perpendicular to the wire is preferred. All three possibilities preserver the rotational symmetry of the wire (the wire looks the same from all directions in the plane perpendicular to the wire).
The second and third options can be eliminated, because we expect the electric field lines to have at least a radial component, since we expect that a negative charge would be attracted to the wire. The electric field will thus look like that illustrated in Figure \PageIndex{5}.
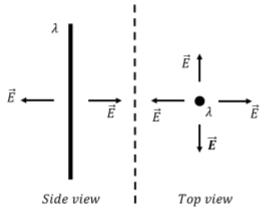
Next, we need to choose a gaussian surface in order to apply Gauss’ Law. A convenient choice is a cylinder (a “pill box”) of radius, R, and length, L, as shown in Figure \PageIndex{6}, as this goes through a point that is a distance, R, from the wire (where we are asked for the electric field). At all points on the cylindrical surface, the electric field vector is either perpendicular or parallel to the surface.
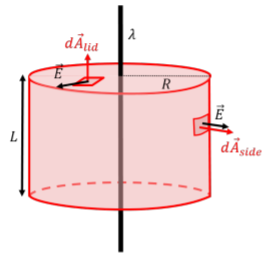
We can think of the cylindrical surface as being composed of three surfaces: 2 disks on either end (the lids of the pill box), and the curved surface that makes up the side of the cylinder. The flux through the entire cylindrical surface will be the sum of the fluxes through the two lids plus the flux through the side:
\begin{aligned} \oint \vec E\cdot d\vec A = \int_{side} \vec E\cdot d\vec A + \int_{lid}\vec E\cdot d\vec A + \int_{lid}\vec E\cdot d\vec A\end{aligned}
where you should note that the closed integral (\oint) was separated into three normal integrals (\int) corresponding to the three “open” surfaces that make up the closed surface. Again, remember that the flux is proportional to the net number of field lines exiting/entering the closed surface, so it make sense to count those lines over the three open surfaces and add them together to get the total number for the closed surface.
The flux through the lids is identically zero, since the electric field is perpendicular to d\vec A everywhere on the lids. The total flux is thus equal to the flux through the curved side surface, for which the electric field vector is always parallel to d\vec A, and for which the electric field vector is constant in magnitude:
\begin{aligned} \oint \vec E\cdot d\vec A = \int_{side} \vec E\cdot d\vec A =\int_{side} EdA=E\int_{side}dA=E(2\pi R L)\end{aligned}
where we recognized that the side surface can be unfolded into a rectangle of height, L, and width, 2\pi R, corresponding to the circumference of the cylinder, so that the area of the side of the cylinder is given by A=2\pi R L.
Next, we determine the charge inside the volume enclosed by the surface. Since the cylinder encloses a length, L, of wire, the enclosed charge is given by:
\begin{aligned} Q^{enc}=\lambda L\end{aligned}
where \lambda is the charge per unit length on the wire. Putting this altogether into Gauss’ Law gives us the electric field at a distance, R, from the wire:
\begin{aligned} \oint \vec E\cdot d\vec A&=\frac{Q^{enc}}{\epsilon_0} \\[4pt] E(2\pi R L) &= \frac{\lambda L}{\epsilon_0}\\[4pt] \therefore E&= \frac{\lambda}{2\pi\epsilon_0R}\end{aligned}
Note that this is the same result that we obtained in Example 16.3.3 when we took the limit of the finite line of charge having infinite length.
Discussion
In this example, we applied Gauss’ Law to determine the electric field at a distance from an infinitely long charged wire. We used symmetry to argue that the field should be radial and in the plane perpendicular to the wire, and recognized that a cylindrical gaussian surface would exploit the symmetry so that the flux can easily be calculated. We obtained the same result as we did from integrating Coulomb’s Law in Example 16.3.3. However, using Gauss’ Law was much less work than integrating Coulomb’s Law.
Why is it difficult to apply Gauss’ Law to a finite wire?
- It is easy to apply Gauss’ Law to a finite wire.
- Because the flux of a finite wire is undefined.
- Because we do not know the charge density of a finite wire.
- Because the symmetry argument does not hold.
- Answer
Gauss’ Law requires us to choose a “gaussian” surface, but which surface should we choose? Generally, it is useful to choose a surface such that the flux can easily be determined, ideally without having to actually do an integral. If symmetry can be exploited such that \vec E has a constant magnitude and direction relative to d\vec A at every location of the gaussian surface, then \int \vec E \cdot d\vec A will be equal to E A. This is why gaussian surfaces are often of the same shape as the charged object they are enclosing.
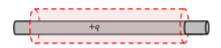
For example, if I need to enclose a cylindrical charge, it would be reasonable to enclose the charge with a cylindrical gaussian surface, as shown in Figure \PageIndex{7}
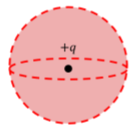
When dealing with point charges which have no shape and are thus spherically symmetric, it makes sense to choose a spherical gaussian surface, as shown in Figure \PageIndex{8}, since the electric field is in the radial direction for a point charge.
Finally, there are some cases of less than ideal choices for the gaussian surfaces. While never wrong, they may require rather complicated integrals to determine the flux. These cases will still provide a correct answer if the situation is modeled correctly.
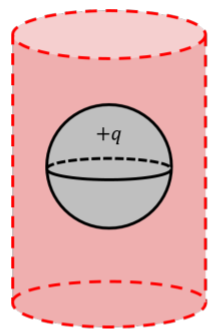
Suppose that I enclose a spherical charge with a cylindrical gaussian surface, as shown in Figure \PageIndex{9}. The electric field will be stronger near the middle of the cylinder’s length than at the center of its endcaps, which means that \vec E is not constant in \int \vec E \cdot d \vec A, so the integral cannot be simplified to EA. A better choice for a gaussian surface in this case would be a sphere, which exploits the symmetry of the charge distribution and provides results in a \vec E of constant magnitude everywhere along the surface. Figures 17.2.7 and 17.2.8 give other examples of when we cannot assume \Phi to be equal to EA.
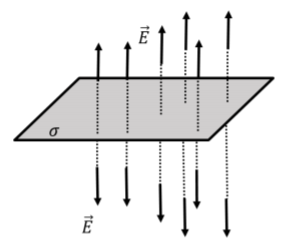
Determine the electric field above an infinitely large plane of charge with uniform surface charge per unit area, \sigma.
Solution
Figure \PageIndex{10} shows a portion of the infinite plane. The electric field vector must be perpendicular to the plane or a preferred direction could otherwise be inferred from the direction of the electric field. We can also argue that the horizontal components of the electric field will cancel everywhere above the plane, since the plane is infinite. The electric field will point away from (towards) the plane, if the charge is positive (negative).
A cylindrical or box-shaped gaussian surface would both lead to the flux integral being easy to calculate, as illustrated in Figure \PageIndex{11}. Indeed, since the electric field is perpendicular to the plane, only the parts of the surface that are parallel to the plane (the lids on the cylinder, the two horizontal planes in the box) will have a net flux through them.
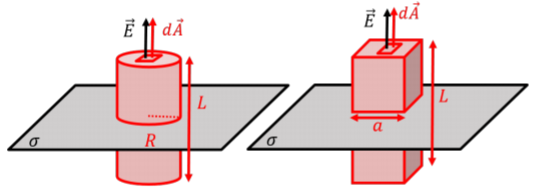
Let us choose a box (right panel of Figure \PageIndex{11}) of length, L, with a square cross-section of side, a. We place the box such that the plane intersects the center of the box (although this is not required, since we already know that the electric field will not depend on distance from the plane). The flux through the box is simply the flux through the two horizontal planes (of area a^2):
\begin{aligned} \oint \vec E\cdot d\vec A&= \int_{top} EdA+\int_{bottom}EdA=2Ea^2\end{aligned}
The box encloses a section of the plane with area a^2, so that the net charge enclosed by the surface is:
\begin{aligned} Q^{enc}=\sigma a^2\end{aligned}
Applying Gauss’ Law allows us to determine the magnitude of the electric field:
\begin{aligned} \oint \vec E\cdot d\vec A&=\frac{Q^{enc}}{\epsilon_0} \\[4pt] 2Ea^2&= \frac{\sigma a^2}{\epsilon_0}\\[4pt] \therefore E&= \frac{\sigma}{2\epsilon_0}\end{aligned}
which is the same result that we found in Example 16.3.4.
Discussion
In this example, we used Gauss’ Law to determine the electric field above an infinite plane. We found that we had a choice of gaussian surfaces (cylinder, box) that allowed us to apply Gauss’ Law. We found the same result that we had found in Example 16.3.4 where we had integrated Coulomb’s Law (twice, once for a ring of charge, then for a disk, then took the limit of the disk radius going to infinity). Again, we see that in configurations with a high degree symmetry, Gauss’ Law can be very straightforward to apply.

