22.1: The Biot-Savart Law
- Page ID
- 19533
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
The Biot-Savart law allows us to determine the magnetic field at some position in space that is due to an electric current. More precisely, the Biot-Savart law allows us to calculate the infinitesimal magnetic field, \(d\vec B\), that is produced by a small section of wire, \(d\vec l\), carrying current, \(I\), such that \(d\vec l\) is co-linear with the wire and points in the direction of the electric current:
\[d\vec B=\frac{\mu_{0}I}{4\pi}\frac{d\vec l\times\hat r}{r^{2}}\]
where, \(\vec r\), is the vector from the element of wire, \(d\vec l\), to the point where we would like to determine the magnetic field, as illustrated in Figure \(\PageIndex{1}\). \(µ_{0}\) is a constant of proportionality called the “permeability of free space”, and has the value \(µ_{0} = 4π × 10^{−7}\text{T} ·\text{m/A}\).
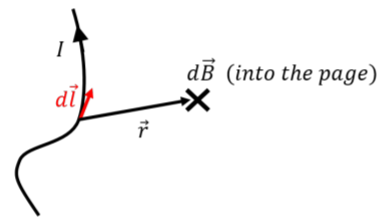
The Biot-Savart Law has some similarities with the Coulomb Law to calculate the electric field, as the magnitude of the magnetic field decreases as the inverse of the square distance between the source and the field. However, it can only be expressed in differential form (i.e. as an infinitesimal), and it requires working in three dimensions, because of the cross product. It is usually more convenient to use the Biot-Savart Law in the form:
\[\begin{aligned}d\vec B = \frac{\mu_{0}I}{4\pi}\frac{d\vec l\times \vec r}{r^{3}} \end{aligned}\]
where the unit vector \(\hat r\) was replaced by \(\vec r/r\).
The procedure for applying the Biot-Savart Law is as follows
- Make a really good diagram, as you will have to include some 3D aspects.
- Choose an infinitesimal section of wire, \(d\vec l\).
- Determine the vector \(\vec r\).
- Determine the cross-product, \(d\vec l ×\vec r\), which will point in the direction of the magnetic field from that infinitesimal section of wire.
- Write out the infinitesimal vector \(d\vec B\), and determine its components.
- Think about symmetry! As you sum the \(d\vec B\), will some components cancel? If yes, you do not need to do those integrals.
- Determine the total magnetic field, component by component, by summing (integrating) the components of \(d\vec B\) over the wire.
Magnetic field from a straight current-carrying wire
In this section, we use the Biot-Savart Law to determine the magnetic field a distance, \(h\), from the center of a finite straight wire of length, \(L\), carrying current, \(I\), as illustrated in Figure \(\PageIndex{2}\).
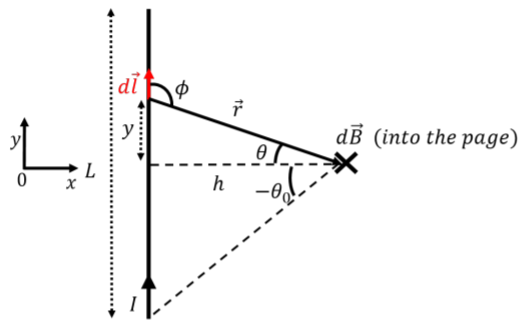
We start by choosing an infinitesimal element of wire, \(d\vec l\), a distance y above the center of the wire, as shown (we choose the origin to be located at the center of the wire). The vector \(d\vec l\) is thus given by:
\[\begin{aligned}d\vec l=dl\hat y \end{aligned}\]
The vector, \(\vec r\), from \(d\vec l\) to the point at which we would like to know the magnetic field is given by:
\[\begin{aligned} \vec r&=r\cos\theta\hat x-r\sin\theta\hat y \\[4pt] r&=\sqrt{h^{2}+y^{2}}=\frac{h}{\cos\theta} \end{aligned}\]
The cross-product between \(d\vec l\) and \(\vec r\) is easily found with the right-hand rule to point into the page (corresponding to the negative \(z\) direction). The magnitude of the cross-product is given by:
\[\begin{aligned} ||d\vec l ×\vec r|| = dlr \sin φ \end{aligned}\]
where \(φ = π/2 + θ\) is the angle between \(d\vec l\) and \(\vec r\), so that \(\sin φ = \cos θ\). The cross-product can thus be written in terms of \(θ\) as:
\[\begin{aligned} d\vec l ×\vec r = −dlr \cos θ\hat z \end{aligned}\]
Note that we can also determine the cross-product algebraically instead of using the righthand rule and the magnitude:
\[\begin{aligned} d\vec l\times\vec r &=(dl\vec y)\times (r\cos\theta\hat x-r\sin\theta\hat y) \\[4pt] &=dlr\cos\theta(\hat y\times\hat x)-rdl\sin\theta(\hat y\times\hat y) \\[4pt] &=-dlr\cos\theta\hat z \end{aligned}\]
The infinitesimal magnetic field element, \(d\vec B\), is given by:
\[\begin{aligned} d\vec B=\frac{\mu_{0}I}{4\pi}\frac{d\vec l\times\vec r}{r^{3}}=-\frac{\mu_{0}I}{4\pi}\frac{dl\cos\theta}{r^{2}}\hat z \end{aligned}\]
Any segment along the wire will result in a magnetic field that is into the page (negative \(z\) direction), thus there will be no cancellations due to any symmetries. We can now proceed to perform the integral.
We can use either \(θ\) or \(y\) to label the wire elements and carry out the integration. We will choose to integrate over \(θ\), requiring us to express \(dl\) and \(r\) in terms of \(θ\) (and constants), as those are the only quantities in \(d\vec B\) that depend on the position of \(d\vec l\). In order to express \(dl\) in terms of \(dθ\), we first relate \(θ\) to \(y\), the position of the wire element:
\[\begin{aligned}y=h\tan\theta \rightarrow dl=dy=\frac{dy}{d\theta}d\theta = \frac{h}{\cos ^{2}\theta}d\theta \end{aligned}\]
and \(r\) is given by:
\[\begin{aligned} r=\frac{h}{\cos\theta}\rightarrow\frac{1}{r^{2}}=\frac{\cos ^{2}\theta}{h^{2}} \end{aligned}\]
Putting this altogether into \(d\vec B\):
\[\begin{aligned} d\vec B=-\frac{\mu_{0}I}{4\pi}\frac{dl\cos\theta}{r^{2}}\hat z =-\frac{\mu_{0}I}{4\pi}\left( \frac{h}{\cos ^{2}\theta}d\theta\right)\left(\frac{\cos ^{2}\theta}{h^{2}}\right)\cos\theta\hat z=-\frac{\mu_{0}I}{4\pi h}\cos\theta d\theta\hat z=dB_{z}\hat z \end{aligned}\]
We define the angle, \(θ_{0}\), to be the maximum amplitude of the angle \(θ\) when integrating over the wire (see Figure \(\PageIndex{2}\)), so that we integrate \(θ\) from \(−θ_{0}\) to \(+θ_{0}\):
\[\begin{aligned} B_{z}=\int_{-\theta_{0}}^{+\theta_{0}} dB_{z}=-\frac{\mu_{0}I}{4\pi h}\int_{-\theta_{0}}^{+\theta_{0}}\cos\theta d\theta =-\frac{\mu_{0}I}{4\pi h}(2\sin\theta_{0})=-\frac{\mu_{0}I}{2\pi h}\sin\theta_{0} \end{aligned}\]
Using the given dimensions:
\[\begin{aligned} \sin\theta_{0}=\frac{L/2}{\sqrt{h^{2}+\frac{L^{2}}{4}}} \end{aligned}\]
Thus, the magnetic field, \(\vec B\), a distance, \(h\), from the center of a wire of length, \(L\), carrying current, \(I\), in the positive \(y\) direction is given by:
\[\vec B=-\frac{\mu_{0}I}{2\pi h}\frac{L/2}{\sqrt{h^{2}+\frac{L^{2}}{4}}}\quad\text{(finite wire)}\]
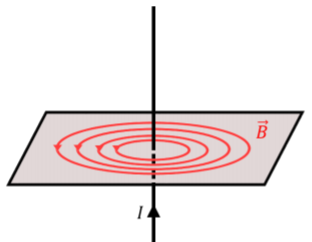
The magnetic field must be rotationally symmetric; that is, if the wire is vertical, the magnetic field at a distance h must look the same regardless of the angle from which we view the vertical wire (we should always see the magnetic field going into the page at the point that we use in Figure \(\PageIndex{2}\)). Thus, the magnetic field lines must form circles around the wire, as illustrated in Figure \(\PageIndex{3}\). Note that the direction of the magnetic field is given by the right-hand rule for axial vectors; when you align your thumb with the current, your fingers curl in the direction of the magnetic field.
It is of particular interest to investigate the limiting case of an infinitely long wire, in the limit of \(L → ∞\), or equivalently, \(θ_{0} → \frac{π}{2}\). The latter is easiest to evaluate, since \(\sin θ_{0} → 1\). The magnitude of the magnetic field, \(\vec B\), a distance, \(h\), from an infinite wire carrying current, \(I\), is given by:
\[B=\frac{\mu_{0}I}{2\pi h}\quad\text{(infinite wire)}\]
One can often make the approximation that the wire is infinite in length, when the distance, \(h\), is small compared to the length, \(L\), of the wire.
Magnetic field from a circular current-carrying wire
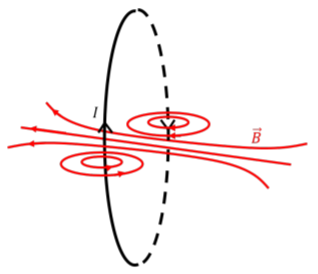
In this section, we examine the magnetic field that is created by a circular current-carrying loop of wire. We can determine the shape of the magnetic field, by considering small sections as straight wires, with circular magnetic field lines around them. As we move closer to the center of the ring, those fields sum together, as illustrated in Figure \(\PageIndex{4}\). Note that the magnetic field from a loop of current is identical to that from a bar magnet (as a bar magnet is, of course, a collection of current loops).
Below, we use the Biot-Savart Law to derive an expression for the magnitude of the magnetic field at a distance, \(h\), from the center of a ring of radius, \(R\), along its axis of symmetry, when there is a current, \(I\), in the ring. While the mathematics are much easier than the case for the straight wire, the challenge in this case is to visualize the calculation in three dimensions! Figure \(\PageIndex{5}\) shows the loop of current, as well as our choice of the coordinate system (with the origin at the center of the ring). In particular, we wish to calculate the magnetic field at a distance, \(h\), along the \(z\) axis. The \(x\) axis goes into the page.
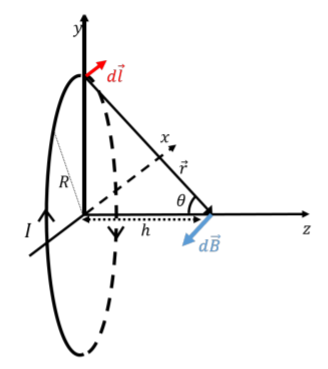
In order to apply the Biot-Savart Law, we choose an element, \(d\vec l\), of wire at the top of the ring, as illustrated. At this position, the element, \(d\vec l\), points in the positive \(x\) direction (into the page):
\[\begin{aligned} d\vec l=dl\hat x \end{aligned}\]
The vector, \(\vec r\), from the wire element to the point where we wish to determine the magnetic field is given by:
\[\begin{aligned}\vec r=-r\sin\theta\hat y+r\cos\theta\hat z \end{aligned}\]
and the angle \(θ\) will be the same for all wire elements along the ring. The cross-product, \(d\vec l ×\vec r\), can be evaluated algebraically:
\[\begin{aligned} d\vec l\times\vec r&=(dl\hat x)\times(-r\sin\theta\hat y+r\cos\theta\hat z) \\[4pt] &=-rdl\sin\theta(\hat x\times\hat y)+rdl\cos\theta (\hat x\times\hat z) \\[4pt] &=-rdl\sin\theta\hat z +rdl\cos\theta (-\hat y) \\[4pt] &=-rdl\sin\theta\hat z-rdl\cos\theta\hat y \end{aligned}\]
so that the element of magnetic field, \(d\vec B\), corresponding to that choice of \(d\vec l\), will lie in the \(y − z\) plane, as illustrated in Figure \(\PageIndex{5}\). Note that the vector \(d\vec B\) is perpendicular to the vector \(\vec r\) (since it is the cross-product of \(\vec r\) with another vector). The magnetic field element, \(d\vec B\), is given by:
\[\begin{aligned} d\vec B&=\frac{\mu_{0}I}{4\pi}\frac{d\vec l\times\vec r}{r^{3}}=\frac{\mu_{0}I}{4\pi r^{3}}(-rdl\sin\theta\hat z-rdl\cos\theta\hat y) \\[4pt] &=\frac{\mu_{0}I}{4\pi r^{2}}(-dl\sin\theta\hat z-dl\cos\theta\hat y)=dB_{z}\hat z+dB_{y}\hat y \end{aligned}\]
As the wire element, \(d\vec l\), moves around the circle, the tip of the resulting magnetic field vector element traces a circle centered on the \(z\) axis, as illustrated in Figure \(\PageIndex{6}\). Note that, in general, \(d\vec B\) will also have an \(x\) component. Thus, only the \(z\) component of the magnetic field will not be canceled when we sum together the magnetic field elements that come from the different wire elements.
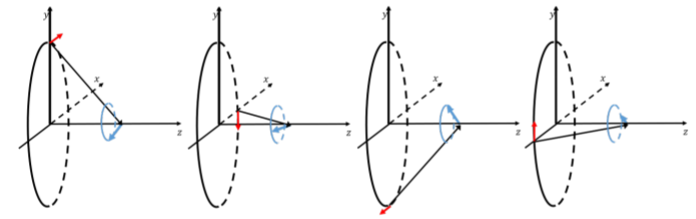
The total magnetic field will be in the negative \(z\) direction, as anticipated from Figure \(\PageIndex{4}\). Summing together the \(z\) components of the infinitesimal magnetic fields:
\[\begin{aligned} dB_{z}&=-\frac{\mu_{0}I}{4\pi r^{2}}dl\sin\theta \\[4pt] B_{z}&=\int dB_{z}=-\int \frac{\mu_{0}I}{4\pi r^{2}}dl\sin\theta \end{aligned}\]
Note that in this case, both \(r\) and \(θ\) are constant for all of the \(d\vec l\), allowing us to take them out of the integral. The integral is then just a sum of the dl elements, which must add up to the circumference of the ring:
\[\begin{aligned} B_{z}=\int dB_{z}=-\frac{\mu_{0}I}{4\pi r^{2}}\sin\theta \int_{0}^{2\pi R}dl =-\frac{\mu_{0}I}{4\pi r^{2}}\sin\theta (2\pi R)=-\frac{\mu_{0}I}{2r^{2}}R\sin\theta \end{aligned}\]
In terms of the variables that we are given:
\[\begin{aligned} r&=\sqrt{R^{2}+h^{2}} \\[4pt] \sin\theta &=\frac{R}{r}=\frac{R}{\sqrt{R^{2}+h^{2}}} \end{aligned}\]
\[\therefore\vec B=-\frac{\mu_{0}I}{2}\frac{R^{2}}{(R^{2}+h^{2})^{\frac{3}{2}}}\hat z\quad\text{(field from a loop of current)}\]
In this case, the math was relatively straightforward (no substitutions to evaluate the integral), however it is challenging to visualize the problem in three dimensions.
A coil is made of \(N\) loops of current-carrying wire packed closely together. What is the magnetic field at the center of the coil?
- \(\frac{µ_{0}I}{2R}\)
- \(\frac{Nµ_{0}I}{2R}\)
- \(\frac{Nµ_{0}I}{2R^{2}}\)
- \(\frac{µ_{0}I}{R}\)
- Answer

